本文记录数据结构中的堆和相关的常见算法问题。
笔记目的,行文从简 。
内容包括:
本文所说的堆,全部指 二叉堆 。
完全二叉树 ¶
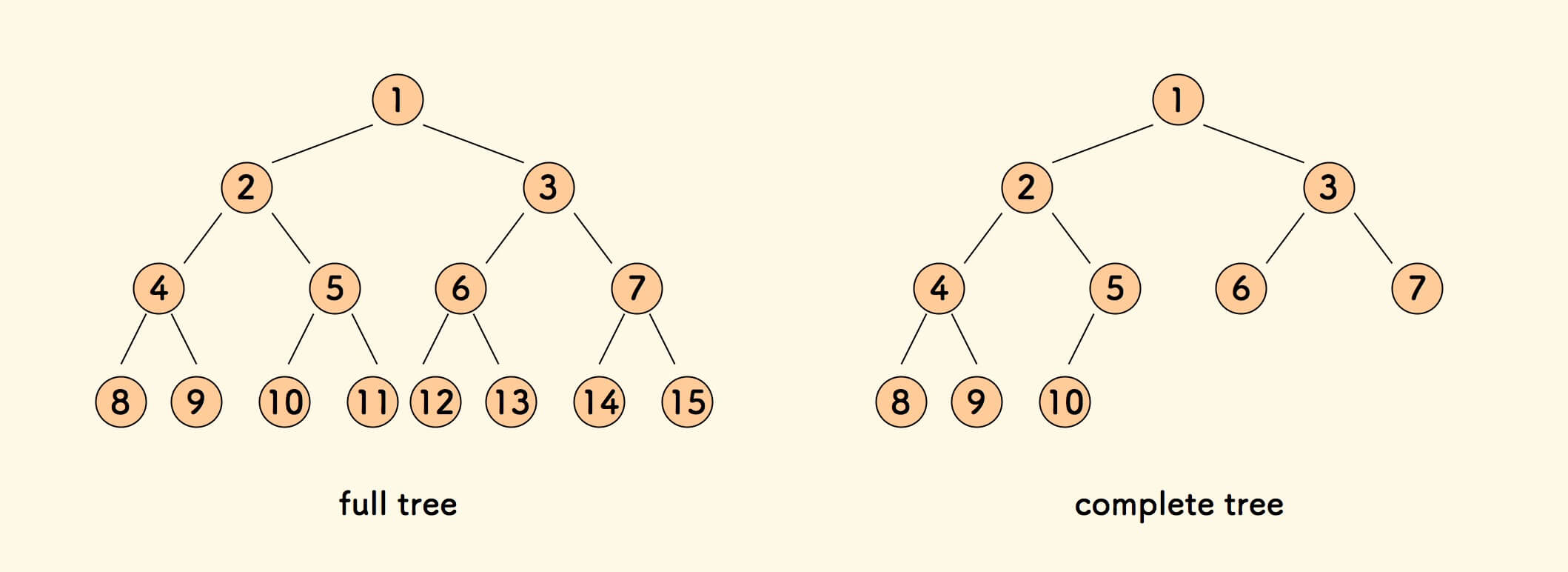
满二叉树 是每一层节点都放满的二叉树。
完全二叉树 是只有最后一层节点右边不放满的二叉树。
简单性质,假设节点总个数是 $n$:
- 满二叉树的最后一层节点数是 $\frac {n+1} {2}$
- 完全二叉树的高度是 $\log{n}$ 。
堆 ¶
- 最小堆:所有父亲节点不比其孩子节点的值大的完全二叉树。
- 最大堆:所有父亲节点不比其孩子节点的值小的完全二叉树。
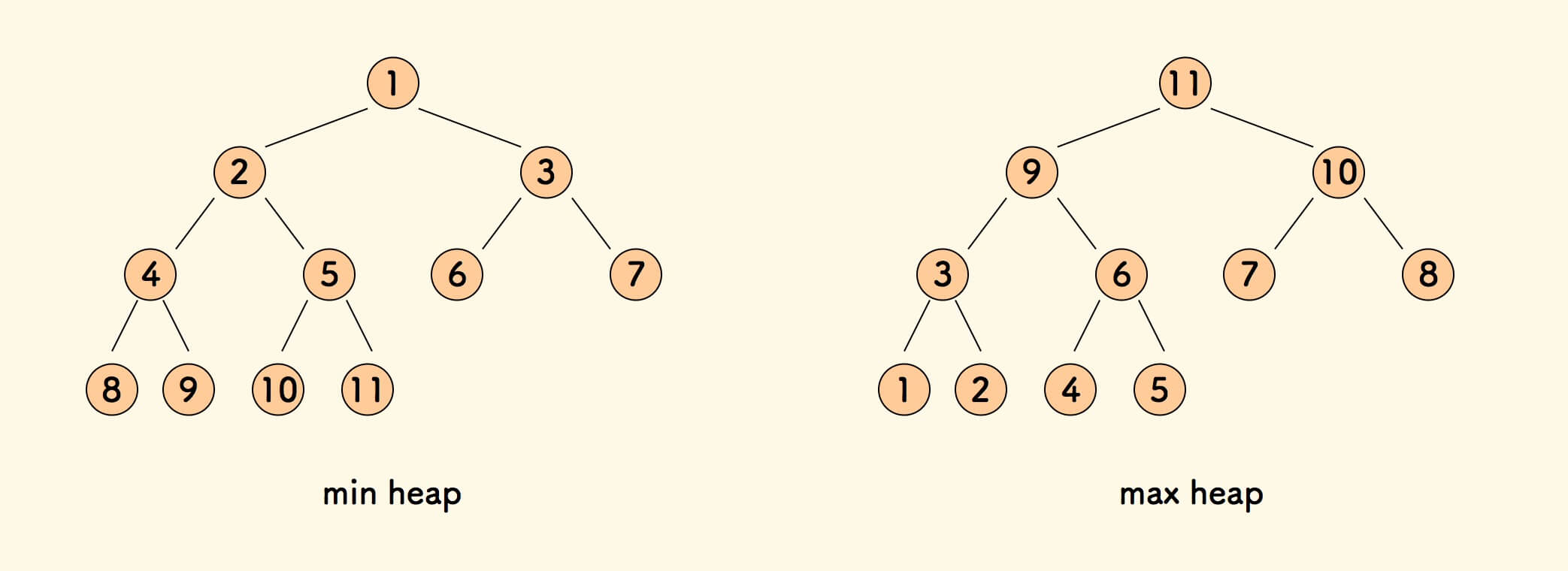
以下只讲最小堆。
数组表示 ¶
完全二叉树是可以用数组来存储的 。
从顶点,自左而右、自上而下进行标号即是对应的数组下标:
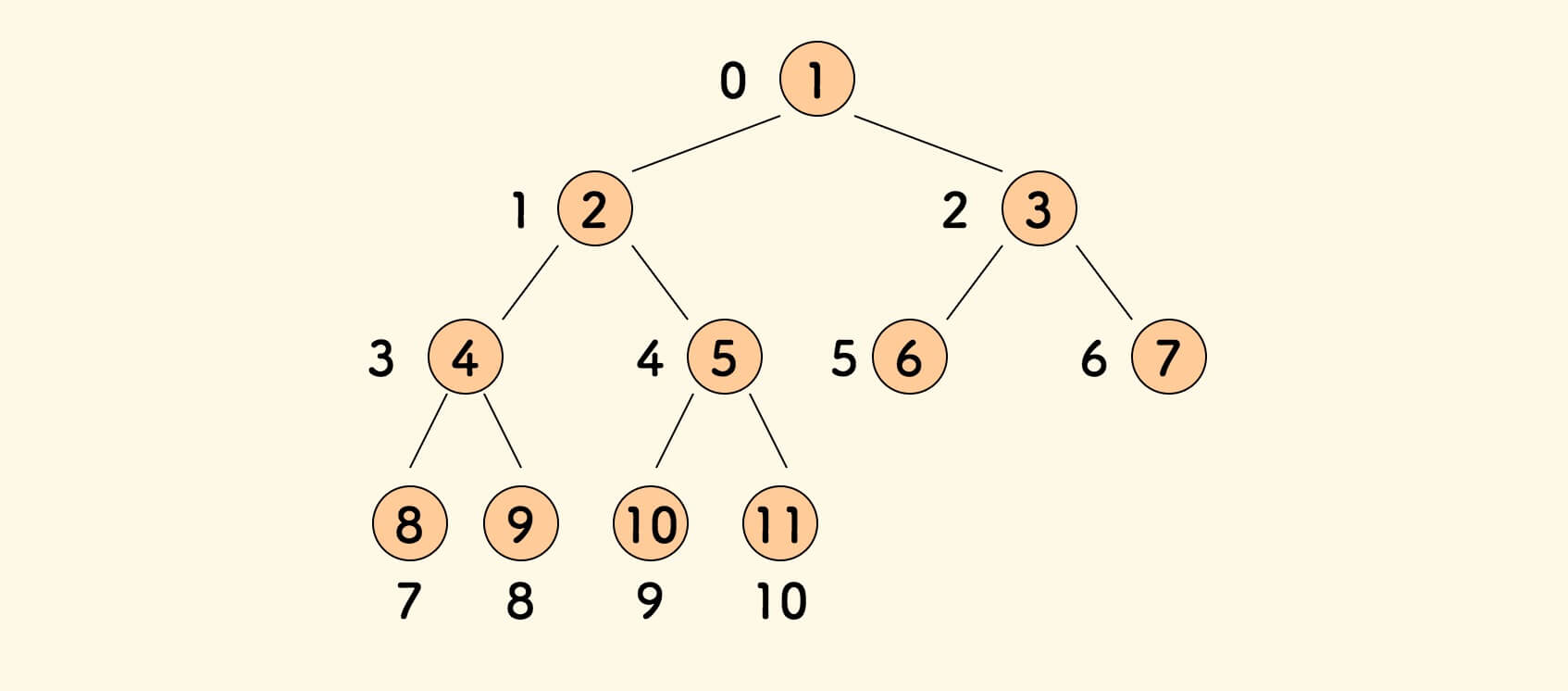
直观的对应示意图:
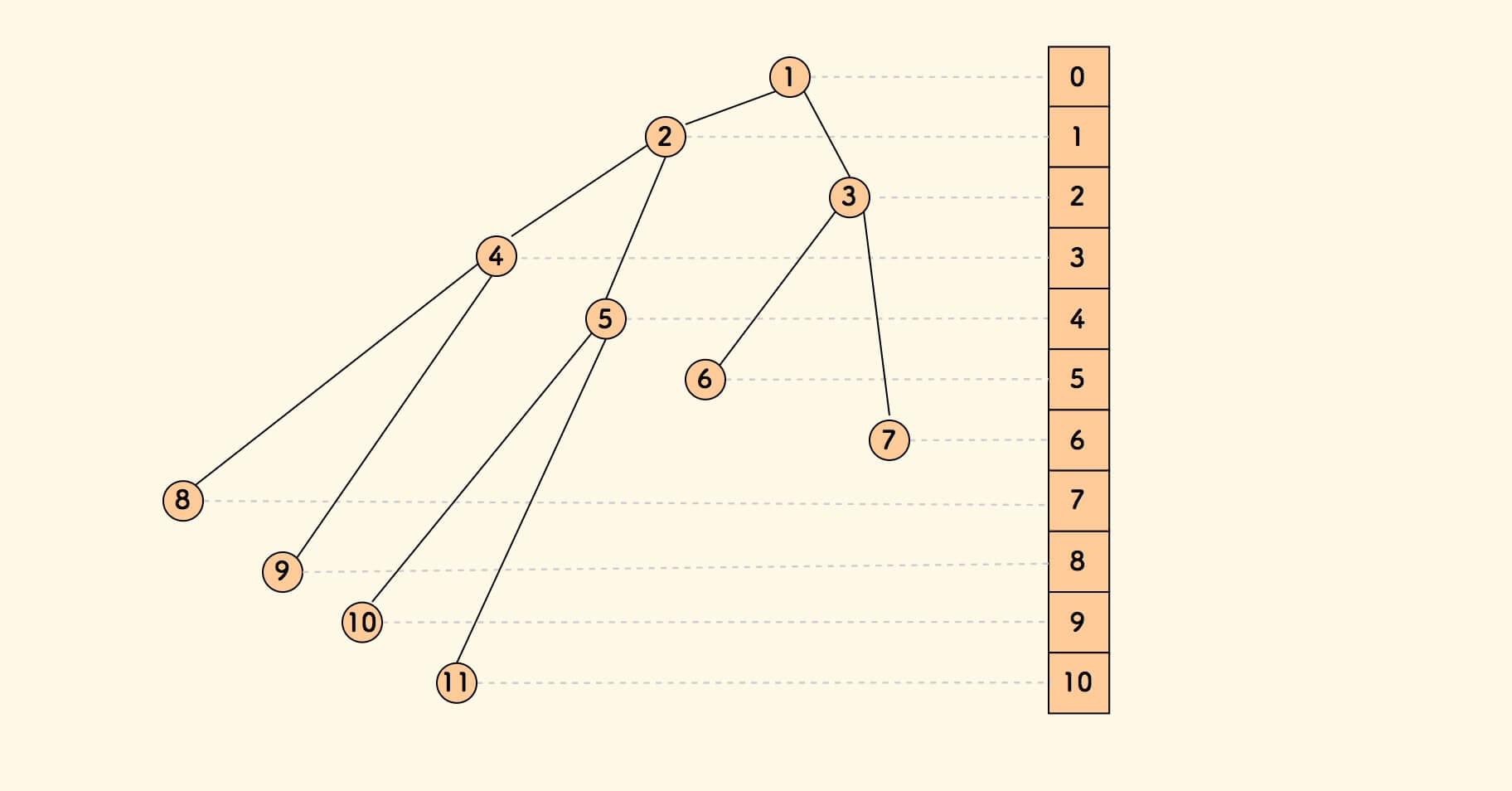
用数组表示时,有如下性质:
- 下标是
i的节点的左右孩子节点的下标是2i+1和2i+2 - 下标是
i的节点的父节点的下标是(i-1)/2(向下取整)
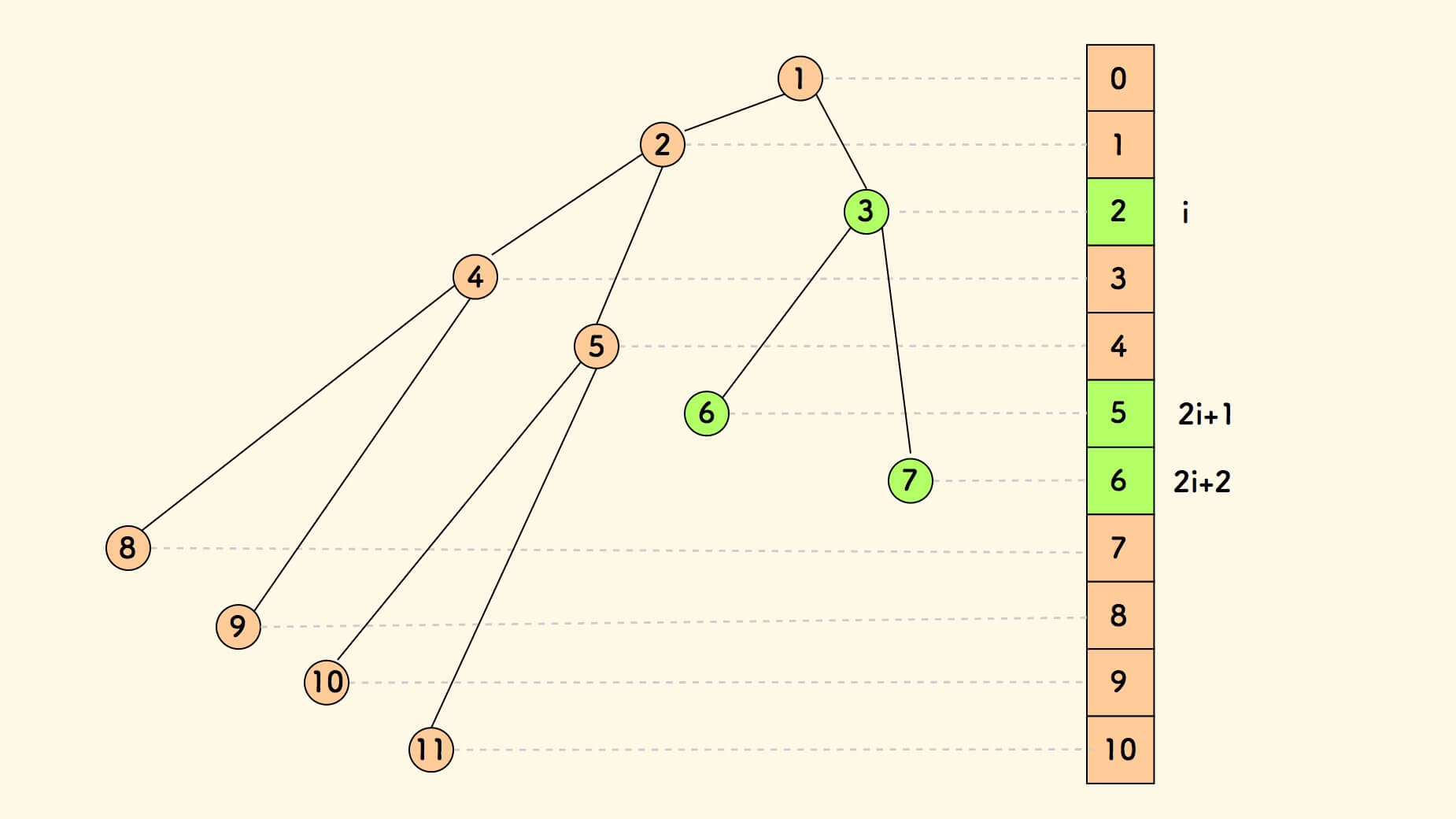
易知,堆顶元素是数组第一项。
最小堆 - 获取最小元素 - C 语言
// 获取堆顶元素 O(1)
int Top(int a[]) { return a[0]; }
插入和上浮 ¶
向一个最小堆插入元素:
- 追加新元素到数组尾部。
- 从新元素处进行堆上浮。
上浮,是指当前元素不断和父节点比较大小:
- 如果父节点更大,则父子交换。
- 否则,满足最小堆性质,停止交换。
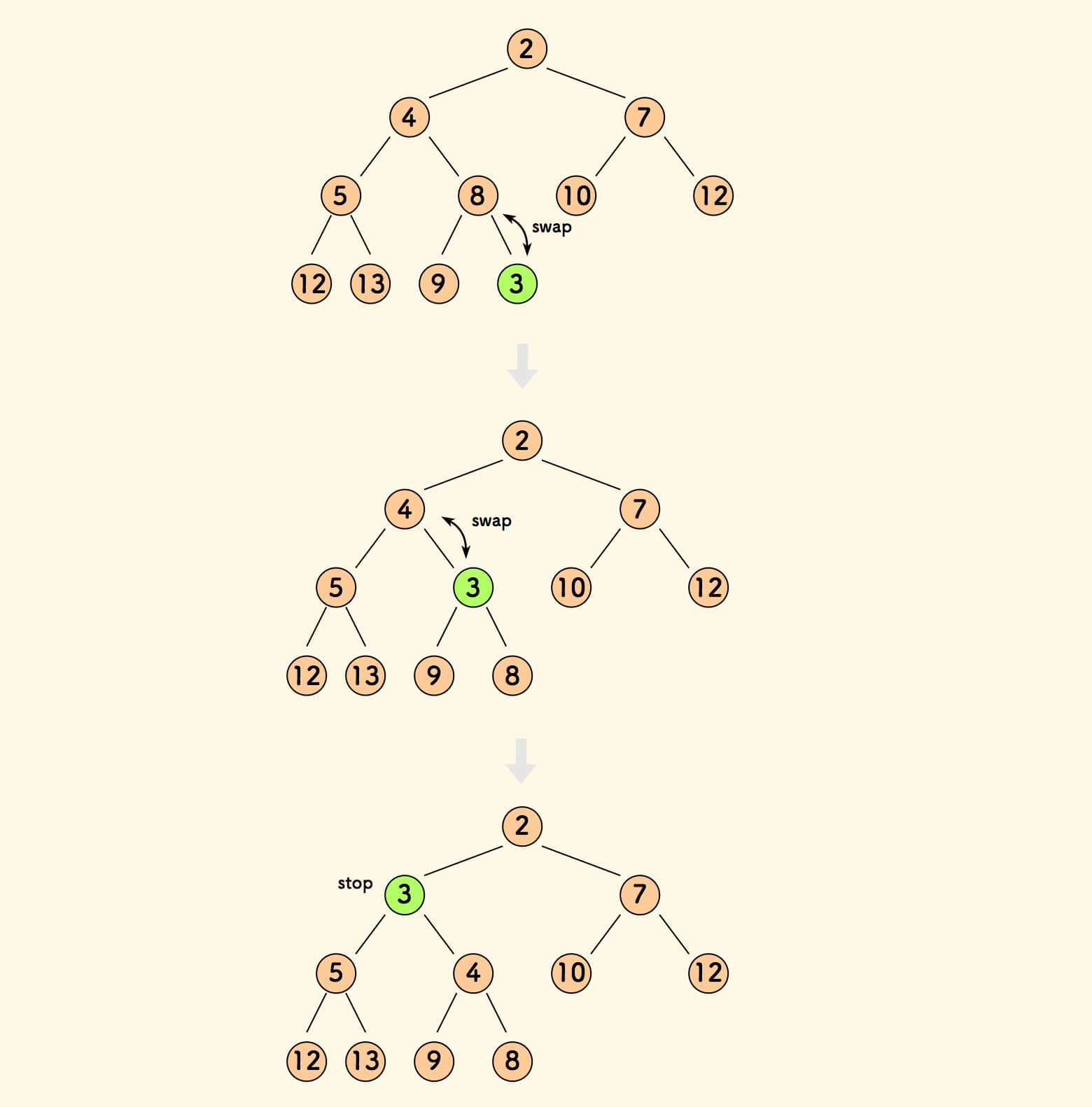
最小堆 - 插入 和 上浮 - C 语言
// 从位置 j 开始上浮堆 O(logn)
void Up(int a[], int j) {
while (j > 0) {
// 父节点
int i = (j - 1) / 2;
if (a[i] <= a[j]) break;
Swap(a, i, j);
j = i;
}
}
// 向大小为 n 的堆 a 中添加元素 v
// 返回添加后的数组大小
int Push(int a[], int n, int v) {
a[n] = v;
Up(a, n); // 上浮
return ++n;
}
一次上浮,最多和所有的父节点交换,共 $h$ 次,时间复杂度是 $O(logn)$ 。
删除和下沉 ¶
从一个最小堆中删除头部元素:
- 尾节点覆盖顶节点,堆大小减一。
- 从顶节点处进行堆下沉。
下沉,是指当前元素不断和两个孩子节点比较大小:
- 如果它比两个孩子节点的值都小,则和更小的孩子交换。
- 否则,满足最小堆性质,停止交换。
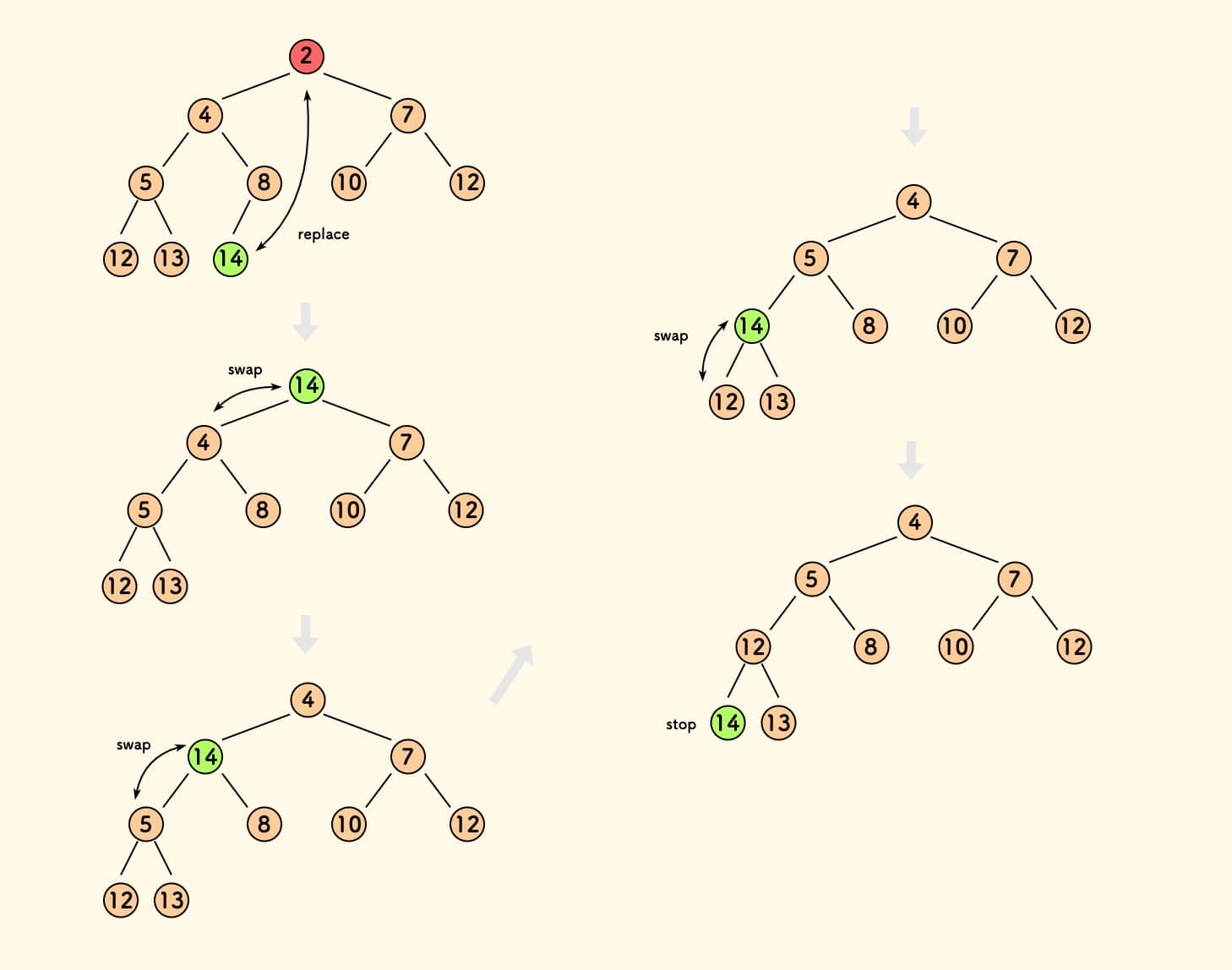
一次下沉,每一层最多和一个孩子交换一次,共 $h$ 次,时间复杂度是 $O(logn)$ 。
上浮和下沉是维护堆操作的基础操作。
最小堆 - 删除 和 下沉 - C 语言
// 从位置 i 开始下沉大小为 n 的堆 O(logn)
void Down(int a[], int n, int i) {
while (1) {
// 左孩子 j1
int j1 = 2 * i + 1;
if (j1 >= n) break;
// 右孩子 j2 (可能不存在)
int j2 = j1 + 1;
// j 是其中值更小的孩子
int j = j1;
if (j2 < n && a[j2] < a[j1]) j = j2;
if (a[i] <= a[j]) break;
Swap(a, i, j);
i = j;
}
}
// 从大小为 n 的堆 a 中移除堆顶元素
// 返回移除的元素。如果堆空,返回 -1
int Pop(int a[], int n) {
if (n <= 0) return -1;
n--;
Swap(a, 0, n);
Down(a, n, 0); // 下沉
return a[n];
}
替换堆顶
如果想要替换堆顶元素呢?
一个直接的做法是,调用一次 Pop 再调用一次 Push 。
这需要一次下沉和一次上浮。
不过,考虑到 Pop 的实现方式,可以直接拿新元素替换堆顶并下沉。
这样,只需要一次下沉。
最小堆 - 替换堆顶 - C 语言实现
// 替换堆顶元素为 v ,返回原堆顶元素
// 如果堆空,返回 -1
// 相对 Pop + Push 更快一些
int Replace(int a[], int n, int v) {
if (n <= 0) return -1;
int top = a[0];
a[0] = v;
Down(a, n, 0);
return top;
}
堆化 ¶
让一个已知数组符合堆性质的一个过程。
一个简单的方式是,新建一个空堆,不断插入数组中的元素,其时间复杂度是 $O(n\log{n})$ 。
常见的方式有两种:
- 自顶向下的上浮。
- 自底向上的下沉。
但是二者时间复杂度不同。
自顶向下的上浮
自上而下的,取每一个孩子节点执行上浮。
从第一个孩子节点开始。
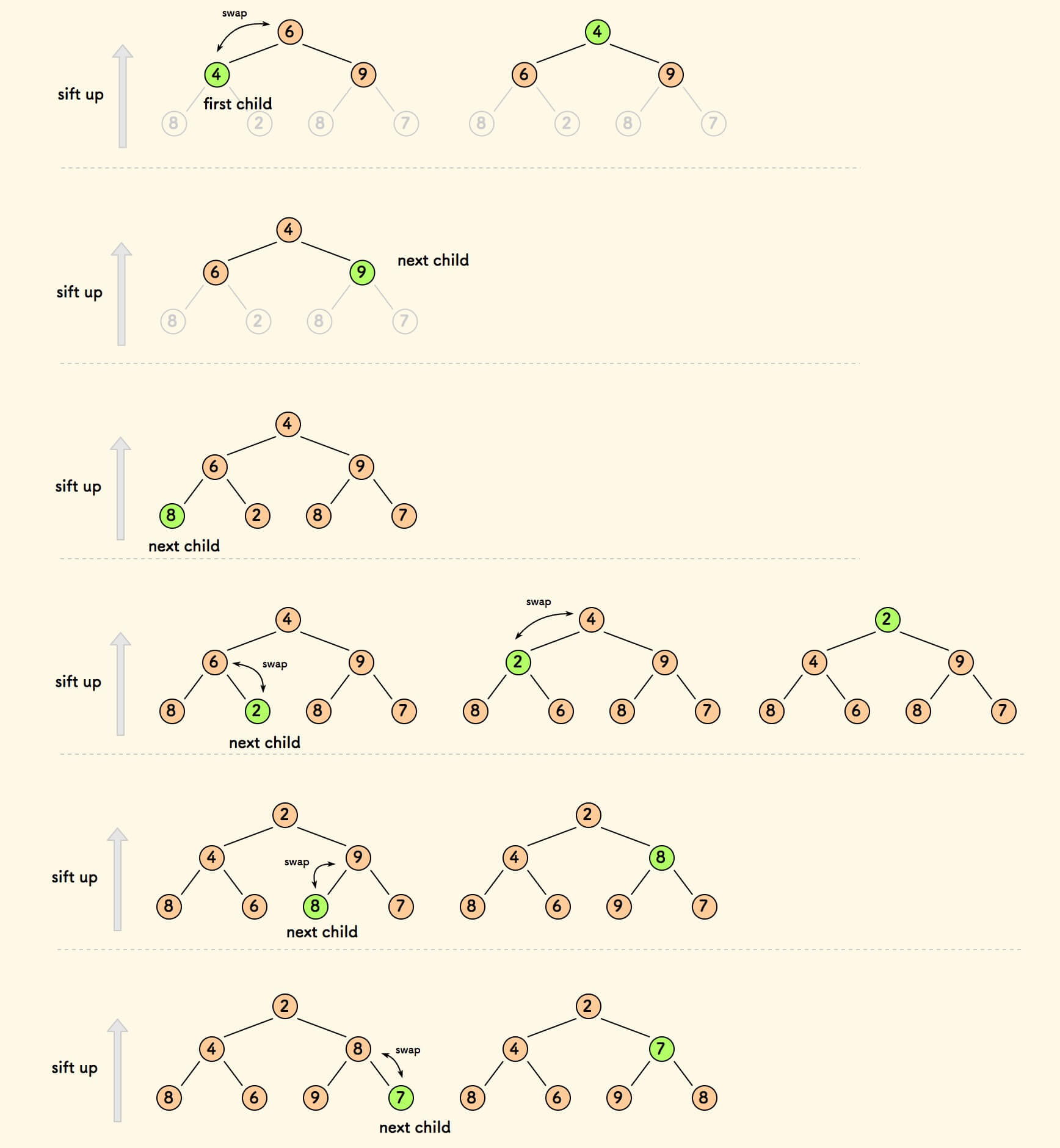
对于第 $k$ 层的孩子节点,一次上浮,需要至多交换 $k$ 次。
第 $k$ 层的节点数是 $2^k$ 个。
假设一共有 $h$ 层,所以总的交换次数是:
\[N = 1 \times 2^1 + 2 \times 2^2 + \ldots + h \times 2^h\]假设共有 $n$ 个节点,取 $h = \log {n}$ ,必然有:
\[N \geq h \times 2^h = n\log{n}\]即这种建堆方式的时间复杂度最好情况下是 $n\log{n}$ 。
所以,一般不采用此方式。
自底向上的下沉
自底向上的,取每一个父节点执行下沉。
从最后一个父节点开始,在倒数第二层最右边。
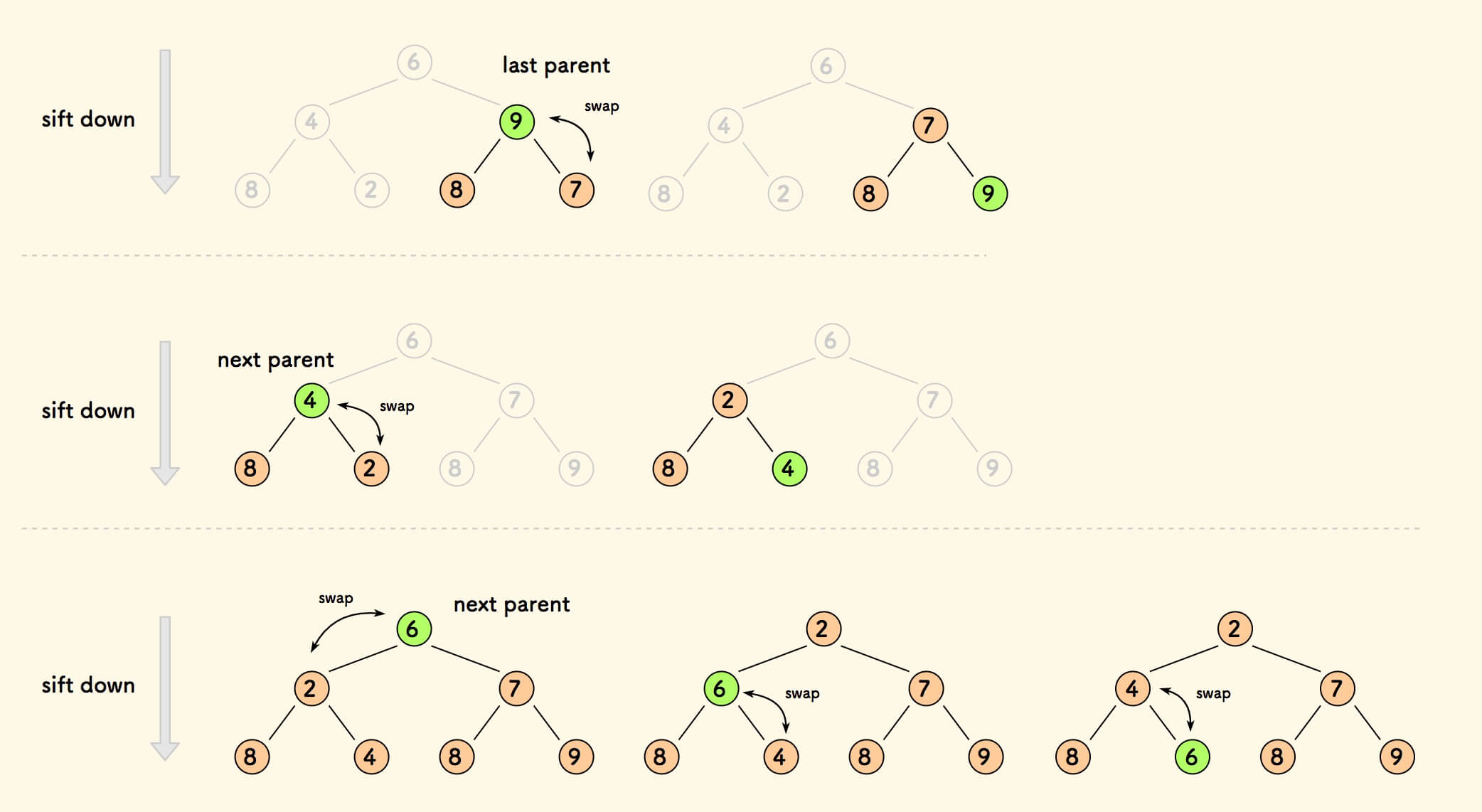
这种方式明显比上一种方式次数少很多。
假设一共有 $n-1$ 个元素,有 $h$ 层。
最后一层有 $n/2$ 个节点,此时一次下沉最多交换 $0$ 次。
倒数第二层有 $n/4$ 个节点,此时一次下沉最多交换 $1$ 次。
依次类推,总的交换次数最多是:
\[N = 0 \times \frac {n} {2} + 1 \times \frac {n} {4} + 2 \times \frac {n} {8} + \ldots + h \times \frac {n} {2^{h}} \\= n \times (0 + \frac {1} {4} + \frac {1} {8} + \ldots + \frac {1} {2^{h}})\]系数是 几何级数 ,一定小于 $1$ 。
所以这种建堆的方式的 时间复杂度最差是 $O(n)$ 。而且显然,建堆的时间复杂度不会比 $O(n)$ 更快, 因为必须要考察每个元素至少一次。 所以说, 堆化过程的时间复杂度总是 $O(n)$ 。
因此,一般采用自底向上,不断下沉的方式来构建堆。
最小堆 - 堆化 - 下沉方式 - C 语言
// 将大小为 n 的数组 a 堆化
void Build(int a[], int n) {
// 从最后一层父节点,不断下沉堆
for (int i = (n - 1) / 2; i >= 0; i--) {
Down(a, n, i);
}
}
小结
- 堆的构建,采用自底向上不断下沉的方式,时间复杂度 $O(n)$
- 插入操作,时间复杂度是 $O(logn)$
- 删除操作,时间复杂度是 $O(logn)$
- 获取堆顶,时间复杂度是 $O(1)$
以上,全部是原地操作。
最小堆 - 本文最小化实现的堆的一个使用样例 - C 语言
int main(void) {
int n = 6;
int a[32] = {3, 1, 2, 7, 0, 4};
// 堆化
Build(a, n);
// 插入
n = Push(a, n, 6);
// 堆顶
int min = Top(a);
// 不断弹出并打印
while (n > 0) {
int v = Pop(a, n--);
printf("%d ", v);
}
}
模板代码 ¶
常见算法问题 ¶
堆排序 ¶
堆排序是堆最常见的一个应用。
从小到大原地排序数组。
思路: 整个数组最大堆化,弹出头,放到尾,直到堆空 。
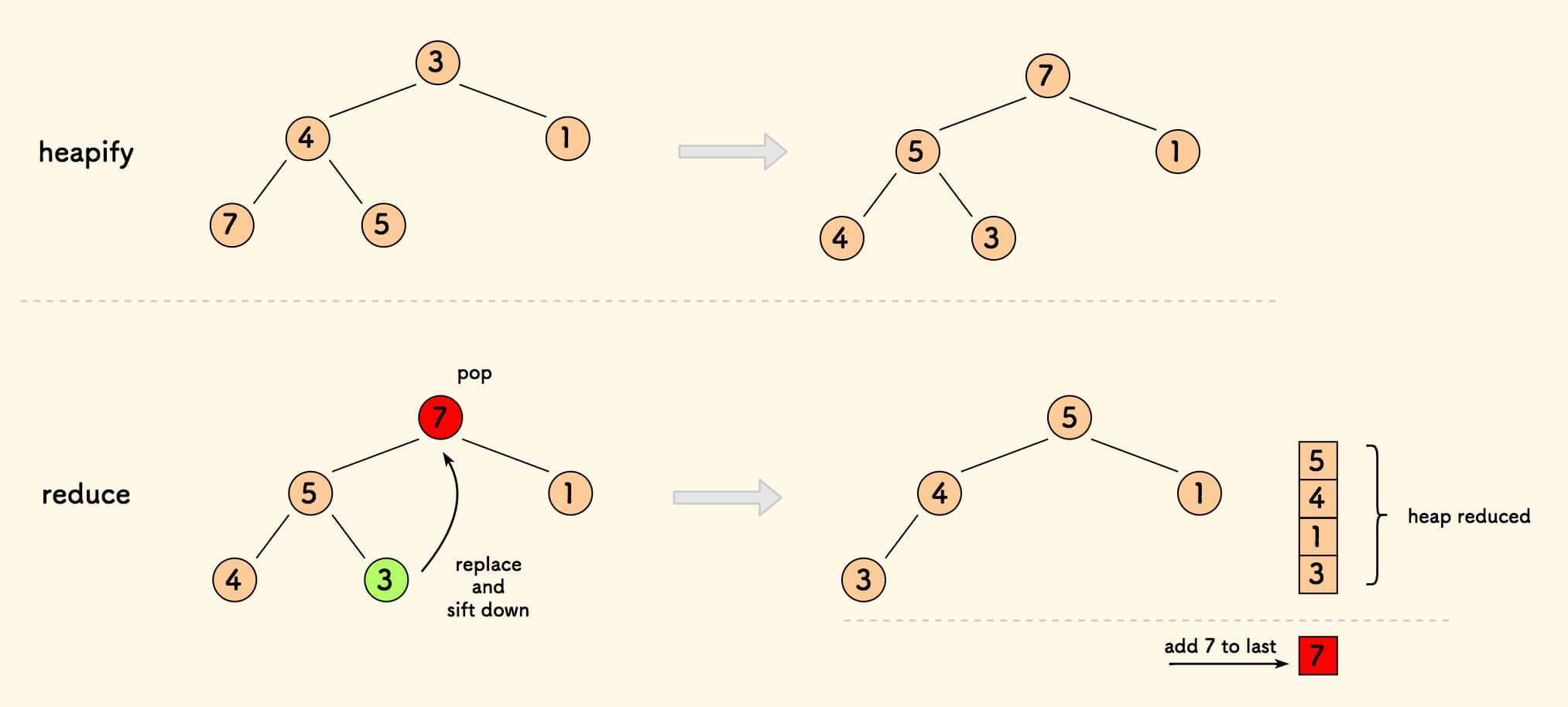
堆排序 - 从小到大原地排序 - C 语言
// 从小到大原地堆排序
// 建立最大堆,弹出头,放到尾
void HeapSort(int a[], int n) {
HeapBuild(a, n);
while (n > 0) {
// 取出顶元素
int v = Pop(a, n--);
a[n] = v; // 放到最后面
}
}
这个思路是原地堆排的思路,即空间复杂度是 $O(1)$ 的。
当然,也可以开一个新数组,多用一些内存,采用最小堆,然后一个一个 Pop 到当前数组。
原地堆排序的方式,亦可以使用最小堆,排完后,元素是从大到小有序的,需要原地反转才可以变成从小到大有序。
所以看起来,简洁的做法,还是 从小到大原地堆排,建立最大堆, 然后依次 Pop 到尾部。
下面分析堆排序的时间复杂度。
首先,依前面所讲,建堆时间复杂度总是 $O(n)$ 。
其次,当剩余 $k$ 个元素时,弹出堆顶,下沉最多 $\log{k}$ 次。
所以,堆排序的总时间最多是:
\[N = n + \log{(n)} + \log{(n-1)} + \ldots + \log{(1)} \\\leq n + n \log{n} \\= n(\log{n}+1) \\= \frac {1} {2} (2n) \log{(2n)}\]也就是,堆排的总时间复杂度最差是 $O(n\log{n})$ 。
又由于堆排序是 基于比较的排序,其时间复杂度不会比 $O(n\log{n})$ 更快, 所以堆排的时间复杂度总是 $O(n\log{n})$ 。
在稳定性上,和 快速排序 一样, 堆化过程中有交换元素的操作,所以堆排序也是不稳定的排序算法 ;稳定性是指,值相同的元素在操作前后的相对顺序应该不变。
不过,相比快速排序,堆排序有一个缺点,就是 局部性差, 我们可以发现,无论是上浮还是下沉的方式,在交换元素的时候, 会导致元素大距离的移动,对实际中的缓存利用不友好。 进一步了解可参考:局部性原理, 知乎 - 为什么在平均情况下快速排序比堆排序要优秀。
TopK 问题 ¶
从一个无序数组中,找出最大的 $k$ 个数。
例如:[5, 1, 2, 4, 3] 中最大的两个数是 [5, 4] 。
这是一个非常经典的算法问题,而且有许多变种:
- 从一个无序数组中找出第 $k$ 大的数。
- 从一个数据流中找出最大的 $k$ 个数。
- 从一个无序数组中找出中位数。
- 从一个无序数组中找出出现次数最多的 $k$ 个数。
一个自然的思路是, 整个数组最大堆化,堆顶弹出 $k$ 个数。
此方法的时间复杂度是 $O(k\log{n})$ ,代码从略。
另一个思路是,
建立大小为 $k$ 的最小堆,把剩余的元素依次和堆顶比较,如果比堆顶大,则替换堆顶 ,最后堆中剩下的就是 $k$ 个最大数。
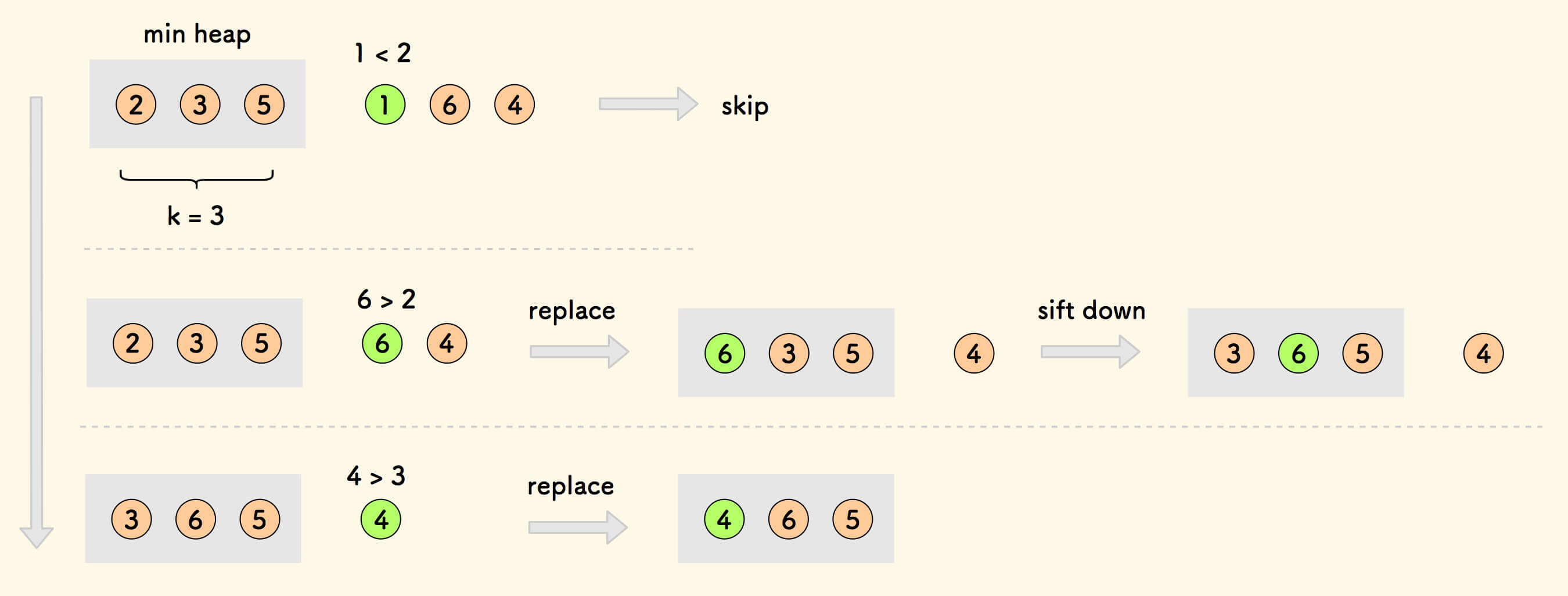
Topk 问题的最小堆方法 - C 语言实现
// 采用最小堆,找出给定数组中的最大的 k 个数
// 函数会原地把 k 大数放到 a 的前 k 个
void TopK(int a[], int n, int k) {
if (n <= 0 || k <= 0 || k > n) return;
// 前 k 个 数最小堆化
HeapBuild(a, k);
// 剩余的 k .. n-1 元素依次和堆顶比较
for (int i = k; i < n; i++) {
if (a[i] > a[0]) {
// 如果比堆顶大,则替换堆顶
HeapReplace(a, k, a[i]);
}
}
}
并且,最终的堆顶元素就是第 $k$ 大元素,也就是 Kth 问题 。
Kth 问题的最小堆方法 - C 语言实现
// 返回无序数组的第 k 大元素
int Kth(int a[], int n, int k) {
TopK(a, n, k);
return a[0];
}
此方法的时间复杂度是 $O(k + (n-k)\log{k})$ ,即 $n\log{k}$ 。
第二种方法, 采用的是过滤的办法, 最小堆当做一个过滤器,留下大的数,剔除小的数。
虽然两种方法在时间复杂度上前者更小, 但是 并不意味着第二种方法更慢 , 第二种方法只有在堆顶更小的情况下才需要进行堆调整 。
对于原数组很大,而 $k$ 很小的情况下,或者数据集大小未知的情况下,比如数据流中找最大的 $k$ 个数时, 数据相对随机的情况下,第二种方法的堆调整次数会更少。此外,第二种方法对空间的要求更小。
性质和场景 ¶
堆的主要应用场景有:堆排序、优先级队列 和 堆置换。
其中第三点,值得驻足品味一番, 所谓堆置换,比如最小堆,就是留下大的,踢出去小的。 前面所说的 TopK 问题、中位数问题,以及 外部排序 都是堆置换的应用。
堆可以作为一个最值过滤器,用有限的局部空间,留下全局最值。
完整代码 ¶
(完)
相关阅读:TopK 问题 - 快速选择方法
本文原始链接地址: https://writings.sh/post/data-structure-heap-and-common-problems
