最大的 K 个数 - TopK 问题

TopK 问题的经典方法有两种， 本文主要记录 快速选择的方法。

采用堆的方法详见 TopK 问题 - 堆置换的方法 。

问题 ¶

从一个无序数组中，找出最大的 $k$ 个数。

例如：[5, 1, 2, 4, 3] 中最大的两个数是 [5, 4] 。

特殊地，寻找中项问题也是一种 TopK 问题。

快速选择的方法 ¶

快速选择的方法，类似 快速排序 的思路：

1. 对数组进行原地分割。

   随机选择一个基准元素，分割后使得：

   大于它的元素都在它左边，小于它的元素都在它右边。

2. 根据分割后左边的元素个数和 $k$ 的大小关系，选择一边递归进行分割。

原地分割

以数组 [5,3,1,9,7,2,5,8,4] 为例， 比如选择第一个元素为基准元素。

原地分割后，大于基准值的放左边，小于基准值的放右边。

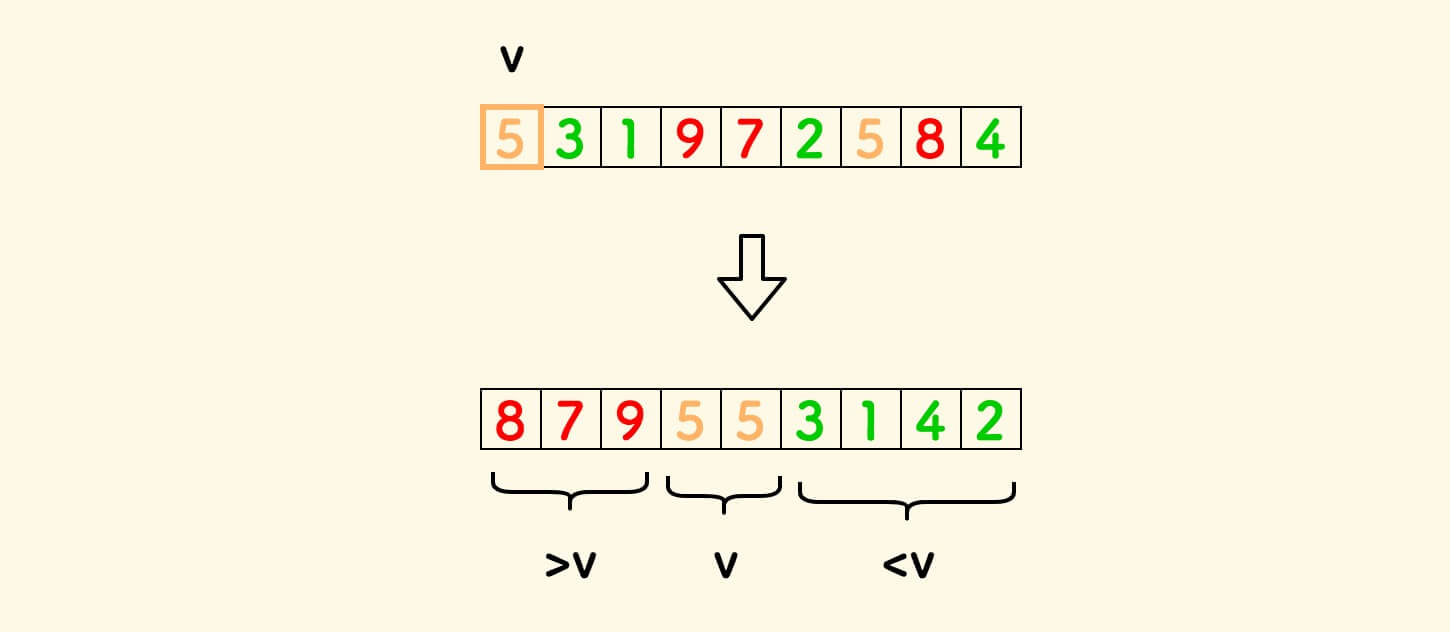
原地分割算法和 快速排序 中的原地分割完全一致。

详细可以参考 原地分割 - 三份 ， 其时间复杂度是 $O(n)$ 。

// 数组原地分割，取 v = a[start]
// >v 在左，=v 在中，<v在右
// 返回基准元素在整个数组中的位置
// 和快排完全一样
int Partition(int a[], int start, int end) {
    int v = a[start];
    int left = start;
    int right = end;
    int i = start;
    while (i <= right) {
        if (a[i] > v) {
            Swap(a, i, left);
            left++;
            i++;
        } else if (a[i] < v) {
            Swap(a, i, right);
            right--;
        } else {
            i++;
        }
    }
    return i - 1;
}

快速选择的主过程

原地分割函数返回的是基准元素在整个数组中的位置 p 。

取 m = p + 1 ，那么 m 表示的就是整个数组中基准元素左边的元素个数。

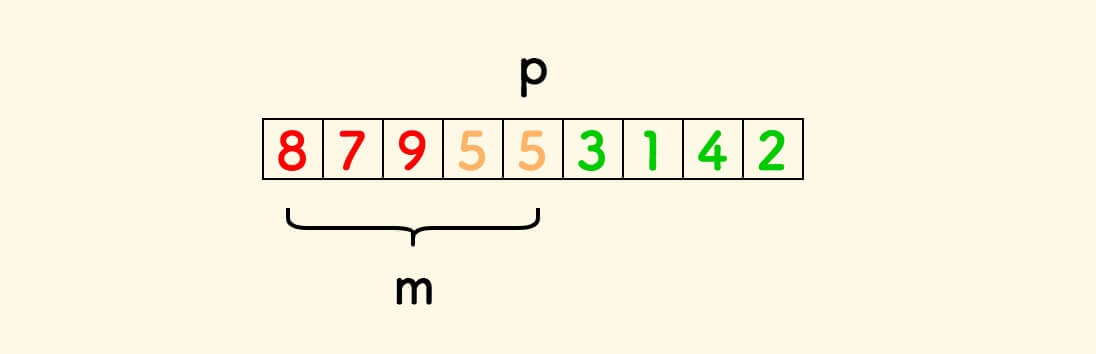
想要求的是整个数组中最大的 $k$ 个数，那么让它和 $m$ 进行比较，有三种情况。

1. 如果 $k = m$ ，那么已经找到最大的 $k$ 个数，终止递归。

   

2. 如果 $k < m$ ，说明最大的 $k$ 个数一定在左边的 $m$ 个数之中。

   但是注意，左边的 $m$ 个数只保证不大于基准元素，并非排序。

   此时，需要对左边的 $m$ 个数递归分割。

   

3. 如果 $k > m$ ，说明已经找到了最大的 $m$ 个数，但是还有 $k-m$ 个数在右边。

   此时，需要对右边的 $m$ 个数递归分割。

   

由此思路，即得出实现代码。

void QuickSelect(int a[], int start, int end, int k) {
    if (start >= end || k <= 0) return;

    int p = Partition(a, start, end);
    int m = p + 1;  // 整个数组中在基准元素左边的元素个数

    if (k < m)
        QuickSelect(a, start, p - 1, k);
    else if (k > m)
        // 注意传 k 而非 k - m ，对齐 m 的意义
        QuickSelect(a, p + 1, end, k);
    else
        return;
}

// TopK 会原地把 k 大数放到 a 的前 k 个
void TopK(int a[], int n, int k) { return QuickSelect(a, 0, n - 1, k); }

复杂度分析

递归深度是 $\log{n}$ ，原地操作，因此空间复杂度是 $O(\log{n})$ 。

每次都只会选择一边进行递归分割，平均来看：

• 第一次选择 $n$ 个元素进行分割
• 第二次选择 $n/2$ 个元素进行分割
• 第二次选择 $n/4$ 个元素进行分割
• ….

每一次的原地分割时间复杂度是线性的 $O(n)$， 因此总的平均时间复杂度是：

其中，系数是 几何级数 ，收敛到 $2$ 。

不同于快速排序的是， 快速排序每次都递归分割两边，而快速选择每次只选择一边递归。

和快速排序算法一样的是，该算法的运行时间依赖于每次随机选择的基准元素。 当数组原本是有序的，而每次总是背运地选择到第一个元素作为基准的话， 每次只能排除一个元素，所以时间复杂度退化为：

结尾语 ¶

对于 TopK 问题，快速选择算法是一种类似快速排序算法的分治算法，不同的是，快速排序每次向两边递归进行， 而快速选择每次只选择一个分支递归下去，其平均时间复杂度是 $O(n)$ ，最坏情况是 $O(n^2)$ 。

最小堆置换的方法 的平均时间复杂度是 $O(nlogk)$， 空间复杂度是 $O(k)$，它更适合大量数据、或者数据集大小未知的情况下的 TopK 问题， 比如 如何留存住数据流中的最大的 K 个 数 等。

（完）

相关阅读: TopK 系列算法问题的总结

本文原始链接地址： https://writings.sh/post/algorithm-topk