最长公共上升子序列 LCIS

本文记录最长公共上升子序列问题，简称 LCIS 问题，是经典的 DP 转移优化案例。

对于两个数列 A 和 B，如果它们都包含一段位置不一定连续的数，且数值是严格递增的，那么称这一段数字是两个数列的公共上升子序列，而所有的公共上升子序列中最长的就是最长公共上升子序列了。求最长公共上升子序列的长度。
进一步地，打印出任意一条最长公共上升子序列。
-- 来自《算法竞赛进阶指南》 · 李煜东-- 洛谷 CF10D， AcWing 272， CodeForces D. LCIS

例如，数列 2,3,1,6,5,4,6 和 1,3,5,6 的一条 LCIS 是 3,5,6，长度是 3。

这是两个经典动态规划问题 LCS 和 LIS 的结合体，其有趣之处在于状态转移的优化。

初步分析 ¶

提前约定，为方便起见，下面 A 和 B 的下标都是从 1 开始。

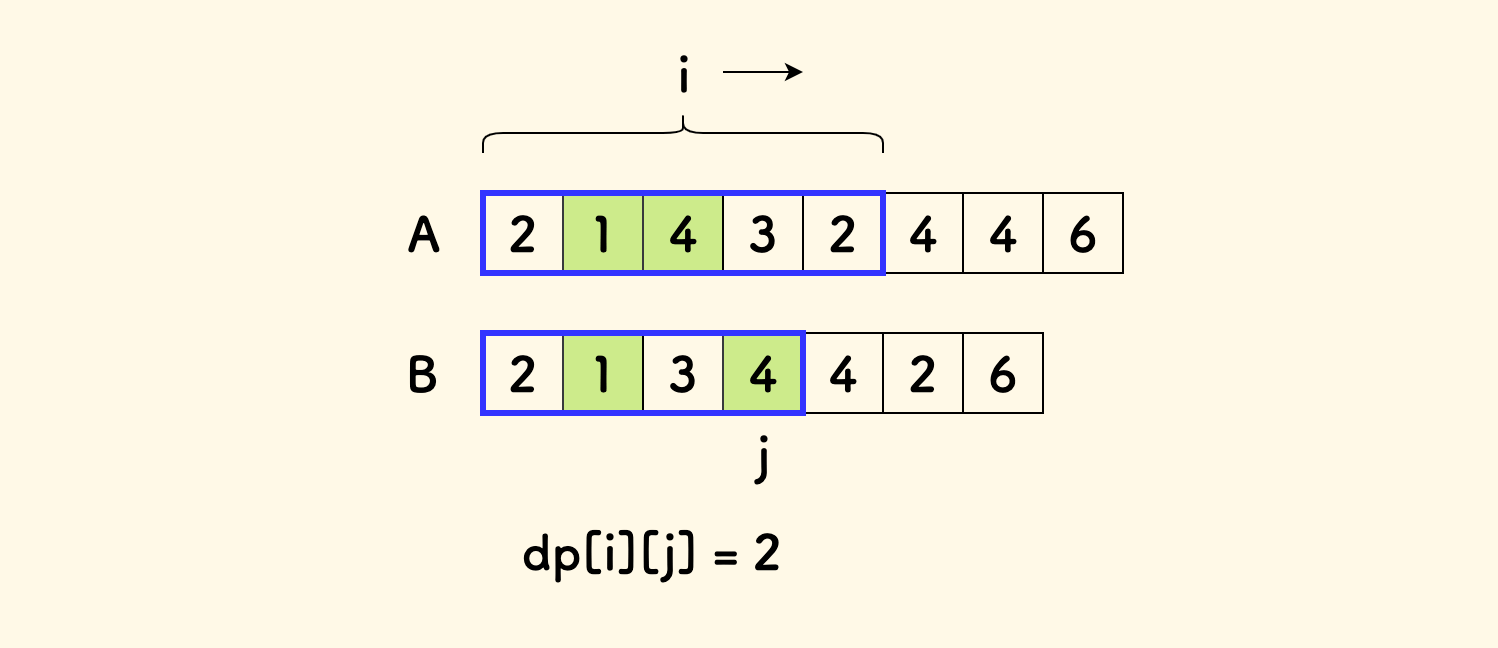
像许多双串 DP 问题一样，设 dp[i][j] 表示 A 中前 i 个数字构成的序列中，以 B[j] 结尾的最长公共上升子序列的长度。

也就是：

以 i 来划分阶段，不断加入新的字符 A[i]。
对 B 数列的每个前缀 B[1..j]，考虑 A 的前缀 A[1..i] 与其形成的、以 B[j] 结尾的 LCIS 的长度。
取所有之最大。

代码框架大概是：

 // 阶段: 不断放入每个 A[i]
for (int i = 1; i <= n; i++) {
    // 考虑 A[1..i] 和 B 的每个前缀形成的以 B[j] 结尾的 LCIS
    for (int j = 1; j <= m; j++) {
        // TODO: 决策 dp[i][j]
        // 答案是所有的 dp 的最大值
        ans = max(dp[i][j], ans);
    }
}

下面分析状态转移：

当 A[i] != B[j] 时，对 B 的前缀 B[1..j] 来说，新加入的数字 A[i] 并没有扩充公共序列的长度，那么以 B[j] 结尾的 LCIS 也更无法扩充。也就是 dp[i][j] = dp[i-1][j]。
当 A[i] == B[j] 时，新放入的 A[i] 扩充了公共序列，需要进一步考虑递增序列是否得到扩充。新放入的 A[i] 可能扩充 B[j] 之前的任何一个递增子序列，需要回溯 B，检查每一个递增子序列，取所有可以和 A[i] 形成新的递增序列的最长的那个，也就是取其中最大 DP 值，再加一。

综合分析下来，代码可以是这样的：

 // 阶段: 不断放入每个 A[i]
for (int i = 1; i <= n; i++) {
    // 考虑 A[1..i] 和 B[1..j] 以 B[j] 结尾的 LCIS
    for (int j = 1; j <= m; j++) {
        // 情况 ①
        if (A[i] != B[j]) dp[i][j] = dp[i-1][j];
        else { // 情况 ②  A[i] == B[j]
            dp[i][j] = 1; // 至少为 1
            for (int k = 1; k < j; k++) {
                if (B[k] < A[i])
                    dp[i][j] = max(dp[i][j], dp[i-1][k] + 1);
            }
        }
        ans = max(dp[i][j], ans);
    }
}

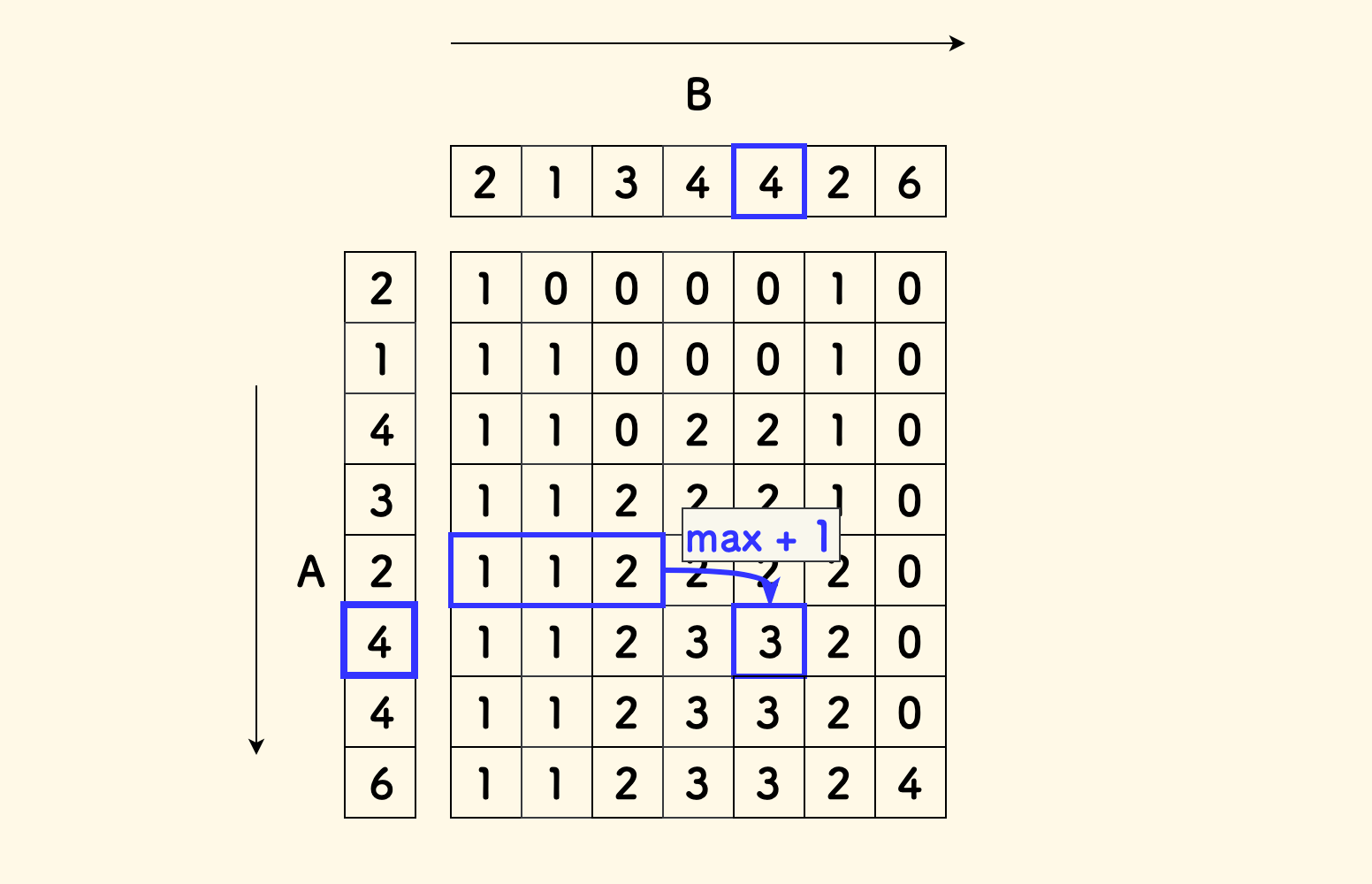
对于双串问题，可以用填表的方式来描述其过程。下面的图示中，DP 的过程的填表方式就是：

自上而下填写每一行，再从左到右填写每个方格。
如果 A[i] == B[j]，则照抄上面方格的数字。
如果 A[i] != B[j]，则检查上一行中 B[j] 左边比 A[i] 小的数字 B[k]，取它们对应方格中数值的最大值，再加一。

转移优化 ¶

但是有一个问题，目前的时间复杂度是 $O\left( nm^{2}\right) $，太慢了。原因在于 DP 转移过程需要的时间就是 $O\left( m^{2}\right)$ 的。

事实上，内层对 B 的两层循环可以优化成一层。这就是本题有趣的地方。

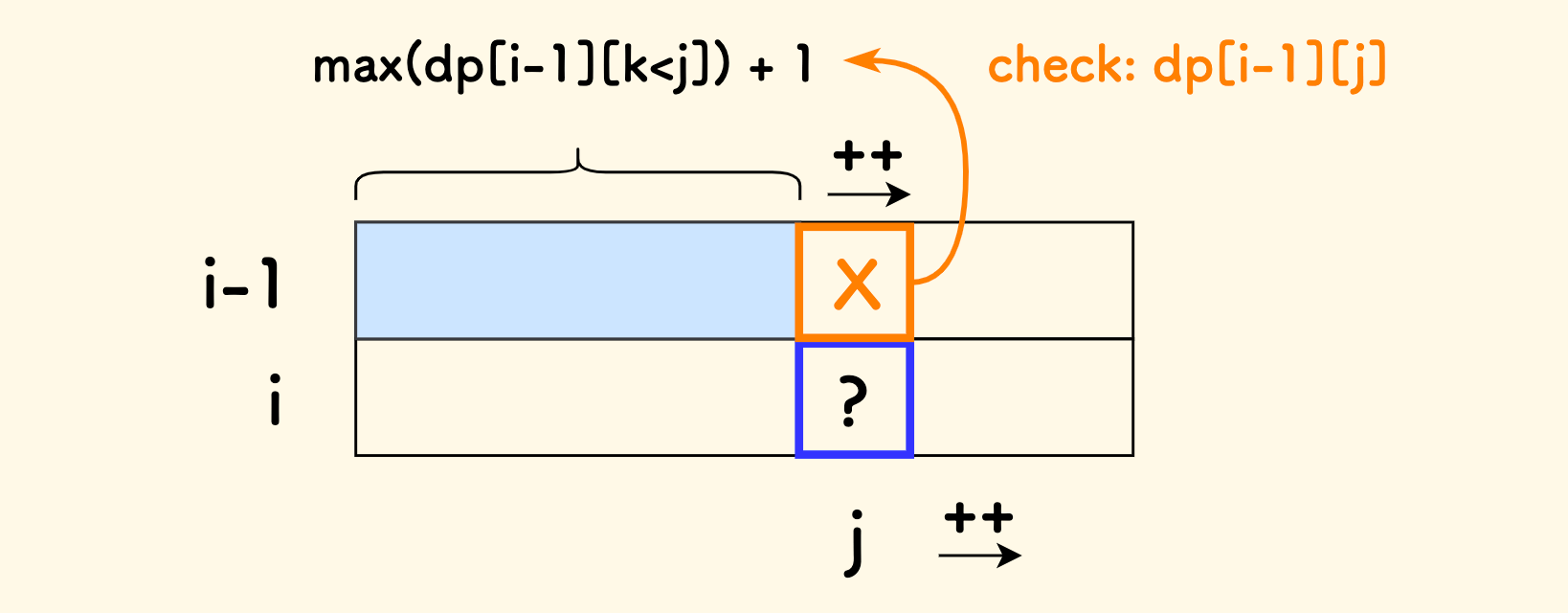
在填表的时候，可以想象有两个齐头并进的指针：当前行有一个，上一行有一个。

上一行的指针负责统计 j 左边满足 B[k] < A[i] 的 dp 最大值，注意到在内层循环中 A[i] 是不变量。

那么可以在：当前行右移 j 的时候，同时把上方格子中的值，加入上一行指针的计算中去，为下一个 j 做好准备。

用代码表示就是：

// 负责统计: 上一行中满足 B[k] < A[i] 的 dp 最大值 + 1
int mx = 0;

for (int j = 1; j <= m; i++) {
    // 当前行指针：决策 dp[i][j]
    // 为上一行满足 B[k] < A[i] 的 dp 最大值 + 1
    // 也就是 mx + 1
    dp[i][j] = mx + 1;

    // 同时维护上一行的指针
    // j 即将增大，可以把其上方的格子加入 mx 的计算中
    if (B[j] < A[i]) mx = max(dp[i-1][j], mx);
}

如此一来，内层两个循环可以优化成一层，转移时间复杂度降低到 $O\left( m\right)$ 。整体时间复杂度则降低到 $O\left( nm\right)$。

究其原因在于：原来的内层的最值计算可以递推，而且恰好可以和外层的 dp 决策齐头并进。

优化后的计算 LCIS 长度的 C++ 代码

for (int i = 1; i <= n; i++) {
    int mx = 0;
    for (int j = 1; j <= n; j++) {
        if (A[i] != B[j]) dp[i][j] = dp[i-1][j];
        else dp[i][j] = mx + 1;
        if (B[j] < A[i]) mx = max(mx, dp[i-1][j]);
        ans = max(dp[i][j], ans);
    }
}

打印 ¶

现在考虑如何输出任意一条 LCIS 。

引用一句动态规划的名言，前面的填表过程也反映了这一点：

每个动态规划背后都隐藏着一个 DAG 结构。 —— 《算法概论》

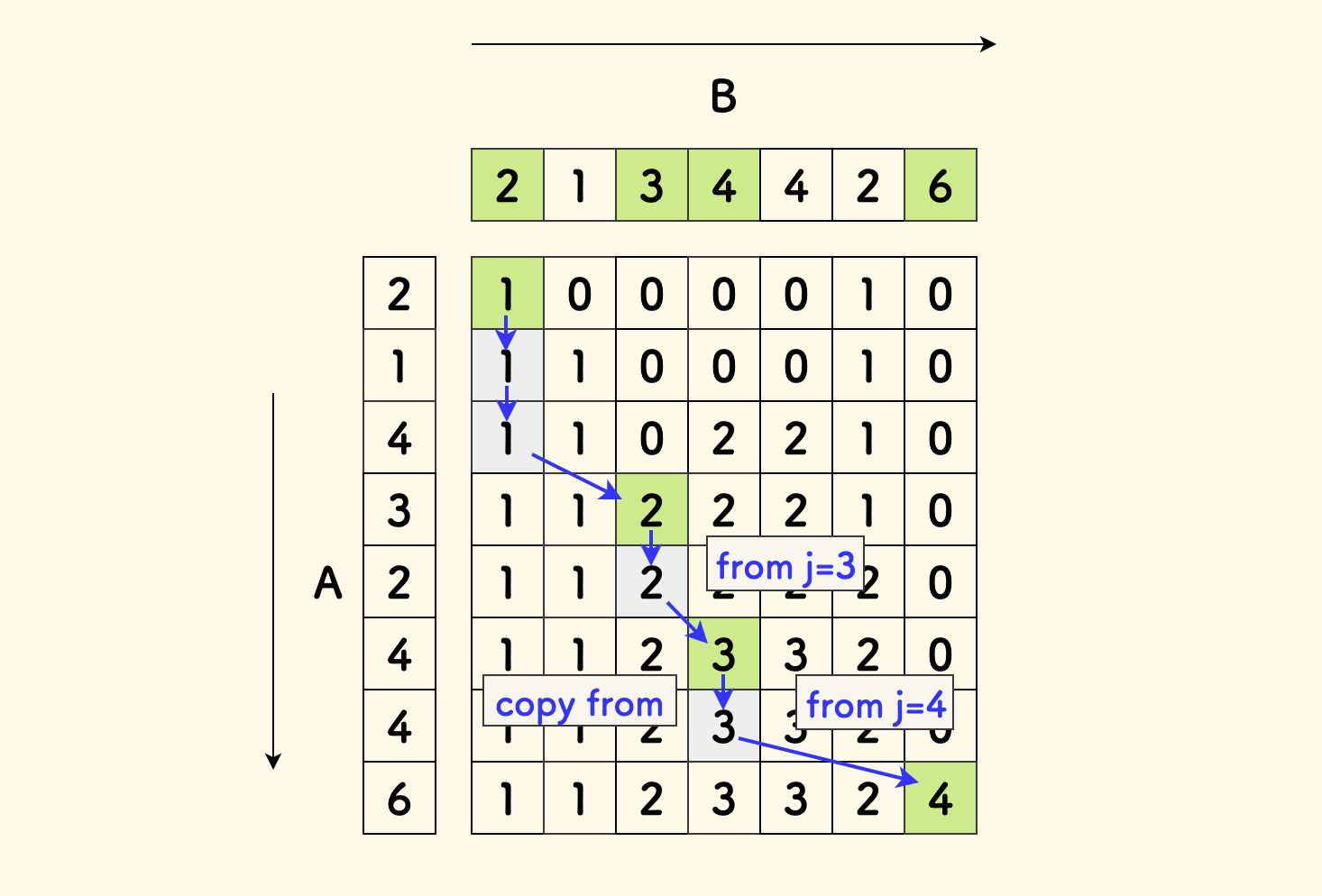
做法是，可以在求长度的同时，用一个路径数组，记录转移来源，最后再从 dp 最大值的格子反向找回去。

不过，因为 LCIS 的含义之一是求公共序列，对于 A[i] != B[j] 条件下途径的元素并不关心，可以直接拷贝上一行方格的来源，只追踪最原始扩充点位的来源。

伪代码大概是：

for (int i = 1; i <= n; i++) {
    int mx = 0;
    int mj = 0; // 上一行赢得 max 的 j

    for (int j = 1; j <= n; j++) {
        if (A[i] != B[j]) {
            dp[i][j] = dp[i-1][j];
            // 拷贝转移的根本来源
            path[i][j] = path[i-1][j];
        }
        else {
            dp[i][j] = mx + 1;
            // 记录由扩充点位
            path[i][j] = {i-1, mj};
        }
        if (B[j] < A[i]) {
            if (mx < dp[i-1][j]) // 维护 mj
                mx = dp[i-1][j], mj = j;
        }
    }
}

最后，再反向输出即可，伪代码大概是：

int i, j = ans_i, ans_j; // 初始，取得最长 LCIS 答案的方格
// 反向找回去
while (ans--) {
    stack.push(B[j]);
    {i, j} = path[i][j];
}
// 输出 LCIS
while (!stack.empty()) cout << stack.pop();

所有代码见下方：

LCIS 代码 - github

（完）