最长递增子序列 - 动态规划方法及打印

最长递增子序列也叫做最长上升子序列，是指在一个数组中找到一个子序列，它的数值严格递增，并且使这个子序列的长度尽可能长。最长递增子序列的元素在原序列中不一定是连续的。

例如 A = [10,9,2,5,3,7,101,18] 的最长递增子序列是 [2,3,7,101]，其长度是 4 。

本文记录最长递增子序列的动态规划方法，包括：

求解最长递增子序列长度
打印所有最长递增子序列

关于经典 LIS 问题，本博客已经有三篇文章讲了三种方法

求解最长递增子序列长度 ¶

leetcode 题目 - 最长递增子序列

最长递增子序列有一个性质：最长递增子序列的尾巴元素一定是这个序列中最大的元素。

如果已知一个递增序列和其尾巴元素，向它追加一个值更大的元素，构成的新的子序列也是递增序列。

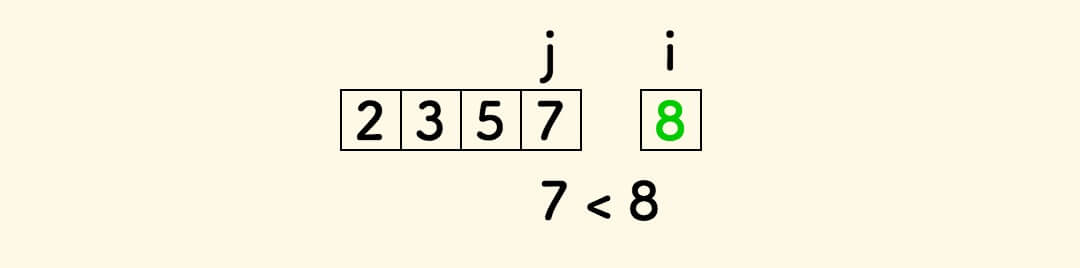
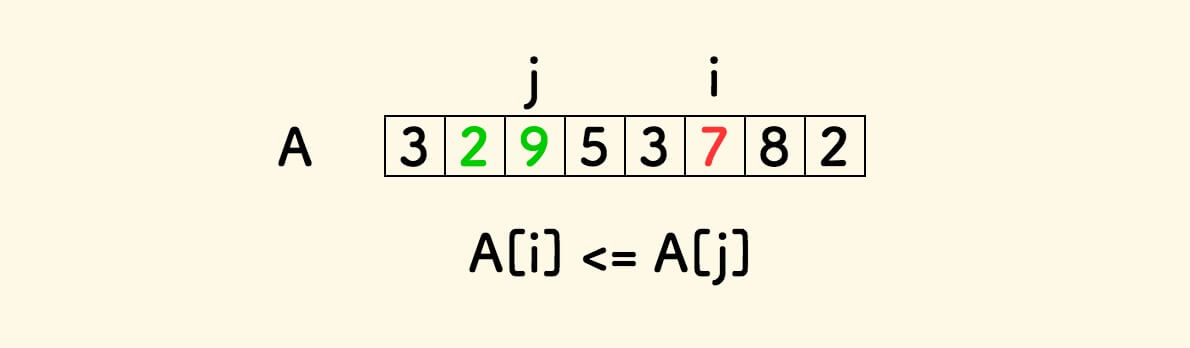
在上图中，新序列是以位置 i 作为尾巴，原来的序列是以位置 j 作为尾巴，其中 j < i 。

所有可以形成的新序列之中最长的，就是以位置 i 结尾的最长递增序列。

这就满足了动态规划方法的最优子结构性质。

下面是具体方法。

构造一维数组， dp[i] 表示以位置 i 结尾的最长递增子序列的长度。

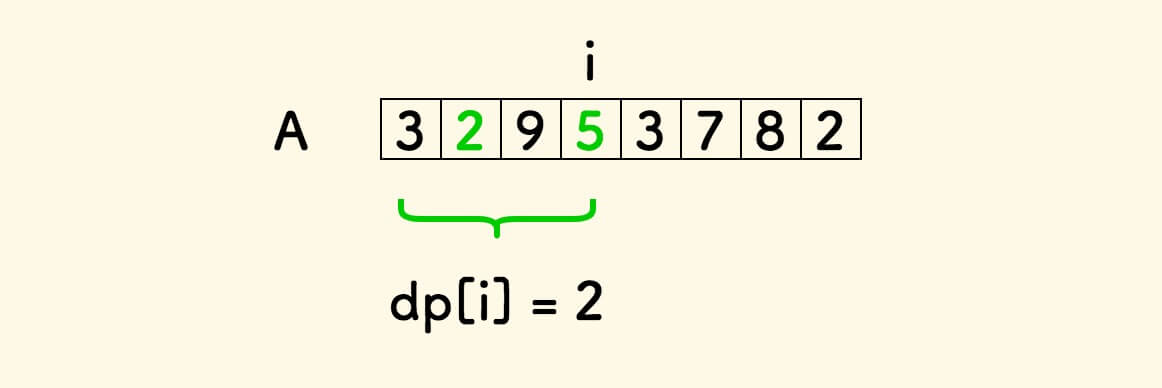
显然， dp[0] = 1 。

考虑如何归纳求解 dp[i] 。

因以位置 i 结尾的最长递增子序列，必以元素 A[i] 结尾，易知 dp[i] 至少为 1 。

假设对于所有小于 i 的 j ，dp[j] 是已计算过的。

如果 A[i] > A[j] ，则最长递增子序列得到扩展，dp[i] 至少为 dp[j] + 1 。

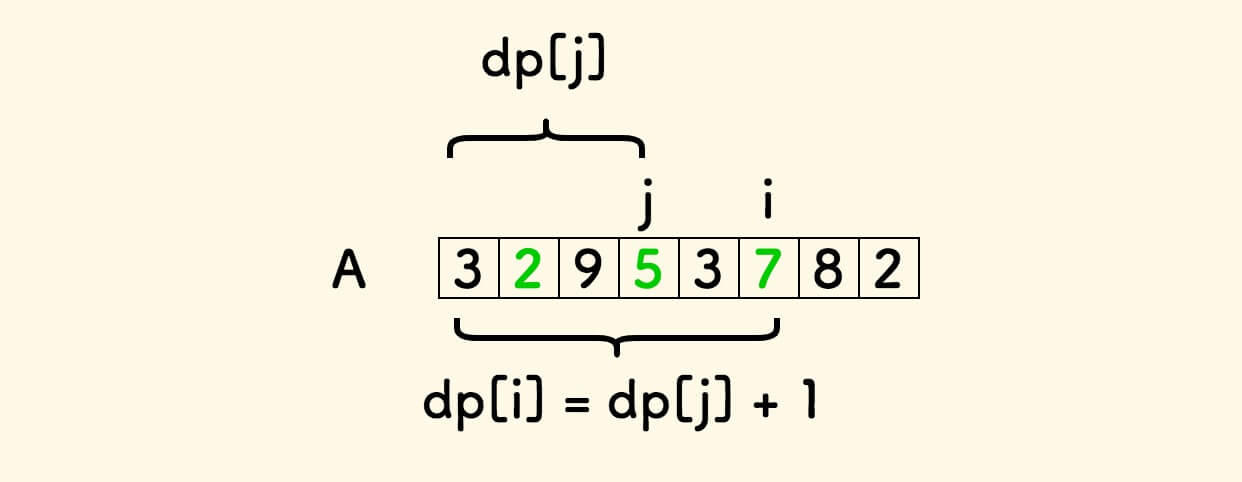
此时，dp[i] 取所有 dp[j] + 1 的最大值即可。

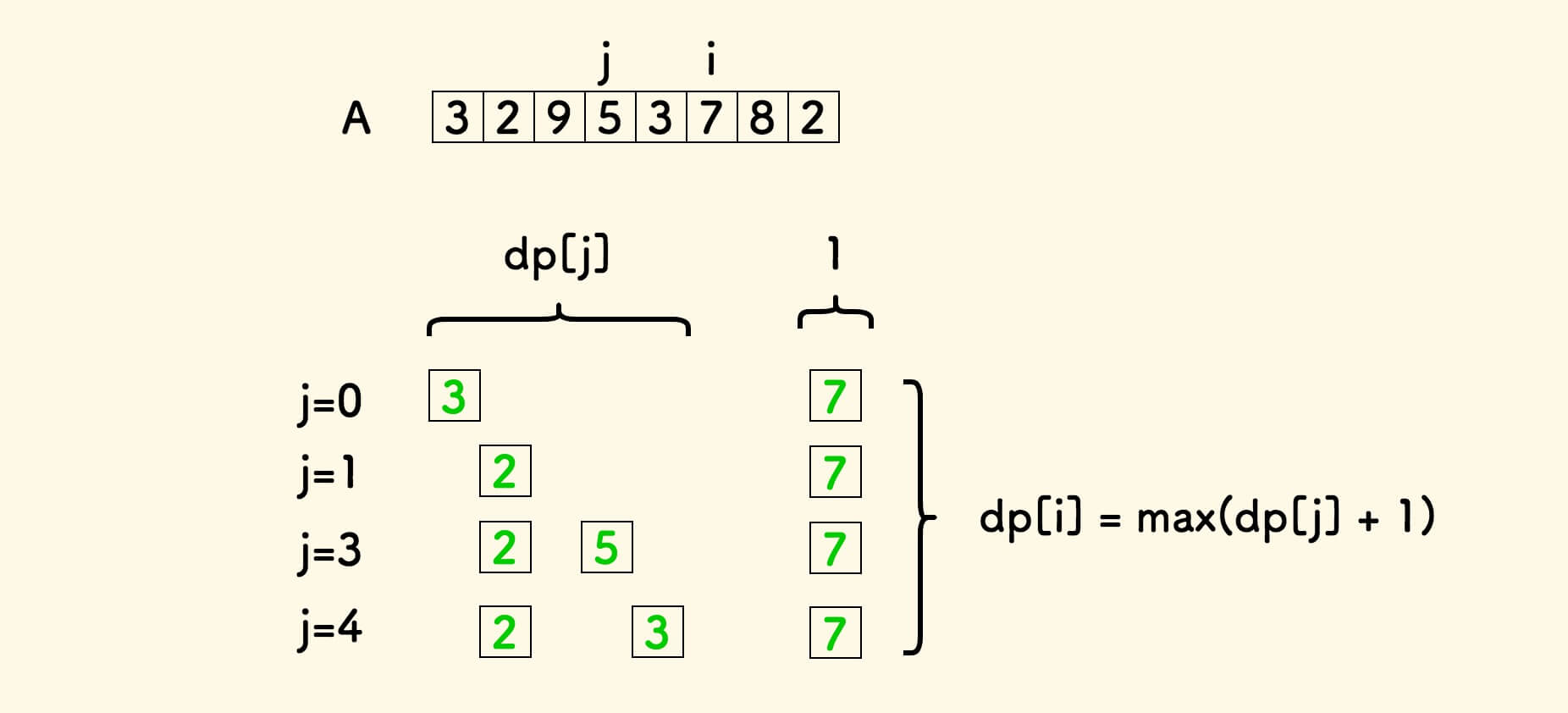
如果遇到 A[i] <= A[j] ，此时无法形成以元素 A[i] 结尾的递增子序列，因此不作考虑。

至此，递推关系已经梳理完毕。

要找的整个数组上的最长递增子序列的长度，就是 dp 数组上的最大值。

显然，时间复杂度是 $O(n^2)$ 。

最长递增子序列 - 动态规划方法 - 求解长度 — C 语言实现

#define max(x, y) (x) > (y) ? (x) : (y)

// 返回长度为 n 的数组 a 的最长递增子序列的长度
int LongestIncreasingSubsequence(int a[], int n) {
    if (n == 0) return 0;

    // dp[i] 代表以位置 i 结尾的最长递增子序列的长度
    int dp[n];
    dp[0] = 1;

    // 记录 dp 中最大值
    int maxdp = dp[0];

    for (int i = 1; i < n; i++) {
        dp[i] = 1;  // 至少为 1
        for (int j = 0; j < i; j++) {
            if (a[i] > a[j]) {
                dp[i] = max(dp[i], dp[j] + 1);
            }
        }
        maxdp = max(dp[i], maxdp);
    }
    return maxdp;
}

注: 求最长递增子序列的长度还有一个 nlog(n) 时间复杂度的解法，见：再探最长递增子序列问题之二分解法。

打印所有最长递增子序列 ¶

如果在动态规划过程中，记住 dp[i] 的计算是源于哪个 dp[j] ，就可以反向追踪出来整个递增序列。

不妨称导致 dp[i] 增加的 j 为 i 的来源位置 。

最长递增子序列可能有多个，一个位置的来源位置也可能有多个。

构建一个二维数组，即路径数组，path[i][k] = j 表示 j 是 i 的一个来源位置。

细节地，path[i] 数组的末尾元素记录为 -2 ，以标记有效元素的结束。

若 i 没有任何来源位置，即 i 只是和自身构成了最长递增序列，那么记一个标志 -1 。

以数组 A = [3, 2, 9, 5, 3, 7, 8, 2] 为例，其 path 数组如下图所示：

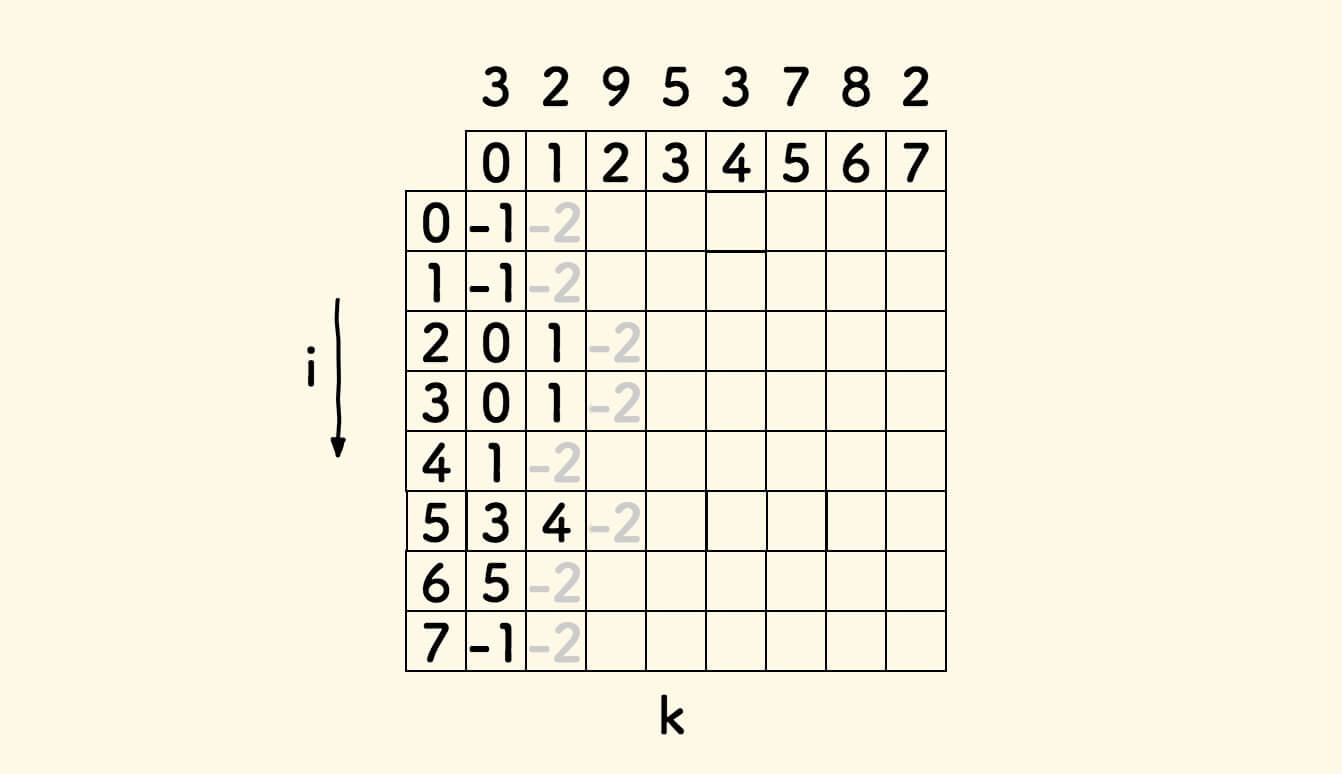
改造 DP 过程代码如下：

最长递增子序列 - 动态规划 - 记录规划路径 — C 语言实现

// 返回长度为 n 的数组 a 的最长递增子序列的长度
int Process(int a[], int n, int dp[n], int path[n][n]) {
    if (n == 0) return 0;
    int maxdp = 0;
    for (int i = 0; i < n; i++) {
        dp[i] = 1;

        // 记录本次从哪个 j 而来，可能有多个
        // k 是记录一个有多少个来源的 j
        int k = 0;

        for (int j = 0; j < i; j++) {
            if (a[i] > a[j]) {
                dp[i] = max(dp[i], dp[j] + 1);
            }
        }

        for (int j = 0; j < i; j++) {
            if (a[i] > a[j] && dp[i] == dp[j] + 1) {
                // 记录 j 为 i 的来源位置
                path[i][k++] = j;
            }
        }

        // 占位 -1 表示 dp[i] 是初始化而来
        if (k == 0) path[i][k++] = -1;

        // 末尾标识结束点
        path[i][k] = -2;

        maxdp = max(dp[i], maxdp);
    }
    return maxdp;
}

假设求解的最长递增子序列的长度是 L ，找到所有 dp[i] = L 的 i 。

即找到所有整个数组的最长递增子序列的尾巴元素的位置 i。

从这些尾巴位置 i 出发，数组 path[i] 中的每个元素 j 即序列中的上一个元素的位置。

不断取 path[i] 中的每个 j 当做新的 i ，反向迭代，即可找出所有的最长递增序列。

下图以 i=5 为例，不断取路径数组中的所有 j 当做新的 i ，就可以找出所有的以位置 i 结尾的最长递增序列。

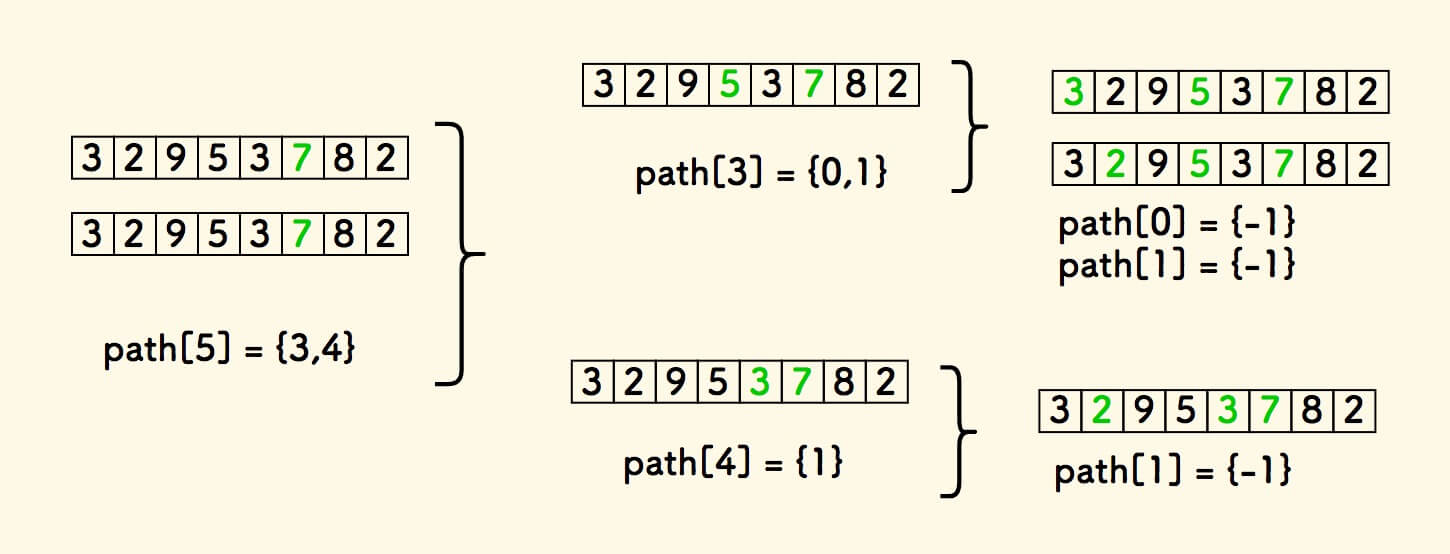
当遇到 path[i] 中的值 -1 时，代表到达了序列头元素，则停止迭代。

反向迭代过程中，用一个栈收集需要打印的数字，最终逆序打印出来即可。

最长递增子序列 - 打印所有最长递增子序列 — C 语言实现

// DFS 深度优先反向追踪路径
// 输入的 z 是需要打印的字符，zn 是其大小
void DFS(int a[], int n, int i, int path[n][n], int z[], int zn) {
    if (i >= 0) {
        // 当前字符需要打印，用 z 栈收集
        z[zn++] = a[i];

        // 处理其所有的来源
        for (int k = 0; path[i][k] != -2; k++) {
            int j = path[i][k];  // 来源位置
            DFS(a, n, j, path, z, zn);
        }
    } else {
        // 需要结束收集，开始逆序打印
        while (zn != 0) printf("%d ", z[--zn]);
        printf("\n");  // 换行作为分割
    }
}

// 打印大小为 n 的数组 a 的所有最长递增子序列
void PrintAllLongestIncreasingSubsequence(int a[], int n) {
    int dp[n];

    // path[i][k] = j 表示 j 是 i 的来源位置
    int path[n][n];

    // 获取最大长度
    int L = Process(a, n, dp, path);

    // 记录需要打印的数字，是一个栈，正向收集，反向打印
    int z[L];
    int zn = 0;

    // 在 dp 数组中找最大长度，然后以其为起点 DFS
    for (int i = 0; i < n; i++) {
        if (dp[i] == L) DFS(a, n, i, path, z, zn);
    }
}

本文中的完整代码 on Github