本文是对换根与二次扫描法的学习笔记。
二次扫描换根法 ¶
一般的树形 DP,通常是深度优先递归整个树,先处理各个子树,然后在回溯时,自下而上地由子节点向父节点进行状态转移。
对于一些 「不定根」 的树形 DP,节点之间的边是无向的,可能需要依次考虑每个节点作为根的情况,最后综合出最优解, 如此做法的时间复杂度是 $O(n^2)$。 但是这种问题往往只需扫描两次,时间复杂度可以优化到 $O(n)$ 。
第一次扫描时,任选一个节点作为根(比如叫做 $root$ ),做一次简单的树形 DP。
此时转移发生在递归的后序(也就是回溯时),由子节点向父节点转移,DP 方向是自下而上进行的。

第二次扫描时,仍从刚才选出的根 $root$ 出发,再进行一次深度优先遍历,自顶向下的修正 DP。
由于第一次扫描的时候,原本的根 $root$ 的 DP 值就已经是最终的正确答案了,但是其他节点 $y$ 缺少考虑来自逆方向的 DP 转移。 也就是下图中从父节点 $x$ 转移到子节点 $y$ 的情况,因为我们要考虑全所有可以到达 $y$ 的可能。

所以,第二次扫描的时候,从已经正确的根 $root$ 向下依次修正所有子节点的 DP 值。
此时转移发生在递归的前序,因为父节点已经得到正确的答案,子节点依赖父节点的 DP 值,所以要先修正父节点,再进入子树递归。
修正的方式是,考虑每个子节点作为整个树新的根,也就是下图中,要从 $f(x)$ 向 $f(y)$ 转移。 经常需要剔除「新根」对其原来的父节点的 DP 贡献,在下图中也就是要从 $f(x)$ 中剔除 $f(y)$ 后再进行转移。
相对于扫描方向来说,DP 是自上而下进行的。

从中可以看到,这种手法要求问题有两个必要特征:
- 针对「不定根树」。
- DP 数值应可以修正,比如是求和、计数等形式时,值是可减的。
代码形式 ¶
首先,存树时可以把无向边算作两个有向边来存:
无向树存边 - C++ 代码
vector<vector<int>> edges(n+1); // 存储点 1~n 的边
for (...) { // 存储边 (x, y)
edges[x].push_back(y);
edges[y].push_back(x);
}
而因为存了两次边,就需要设置一个访问数组 vis,防止重复。
bool vis[N]; // 访问数组
memset(vis, 0, sizeof vis);
C++ 代码形式如下:
void up(int x) {
vis[x] = true;
for (auto y : edges[x]) {
if (vis[y]) continue;
up(y);
// TODO: 后序转移 f(x) ← f(y)
}
}
void down(int x) {
vis[x] = true;
for (auto y : edges[x]) {
if (vis[y]) continue;
// TODO: 前序转移 f(y) ← f(x)
down(y);
}
}
root = 1; // 任选一个节点作为根
up(root); // 第一次扫描,先向上转移
memset(vis, 0, sizeof vis); // 注意清理访问数组
down(root); // 第二次扫描,再向下修正
最大白子树 ¶
一个有 $n$ 个节点的无向树,共有 $n-1$ 条边。每个节点要么是白色的、要么是黑色的。
从一个节点出发,遇到白色节点就加一,遇到黑色节点就减一,最后得到一个数字。你可以自由选择走哪些节点,以使这个数字尽可能大。
问,从每个节点 $ver_i$ 出发时,可以得到的这种数字最大是多少,依次输出。
-- 来自 Codeforces 1324 F. Maximum White Subtree
显然,是一个不定根问题。
定义 $f(x)$ 为从节点 $x$ 出发作为根节点的子树上可以得到的最大结果。
最开始,设置每个节点 $x$ 的权值 $ver(x)$,如果节点是白色的,则设置为 $1$,否则设置为 $-1$。
初始情况下,每个单节点的子树的 DP 值就是其节点权值:
\[f(x) = ver(x)\]选定 $1$ 号节点作为根,进行第一次扫描,假设当前迭代的父节点是 $x$,子节点是 $y$,先递归计算完 $f(y)$,然后向父节点 $x$ 转移:
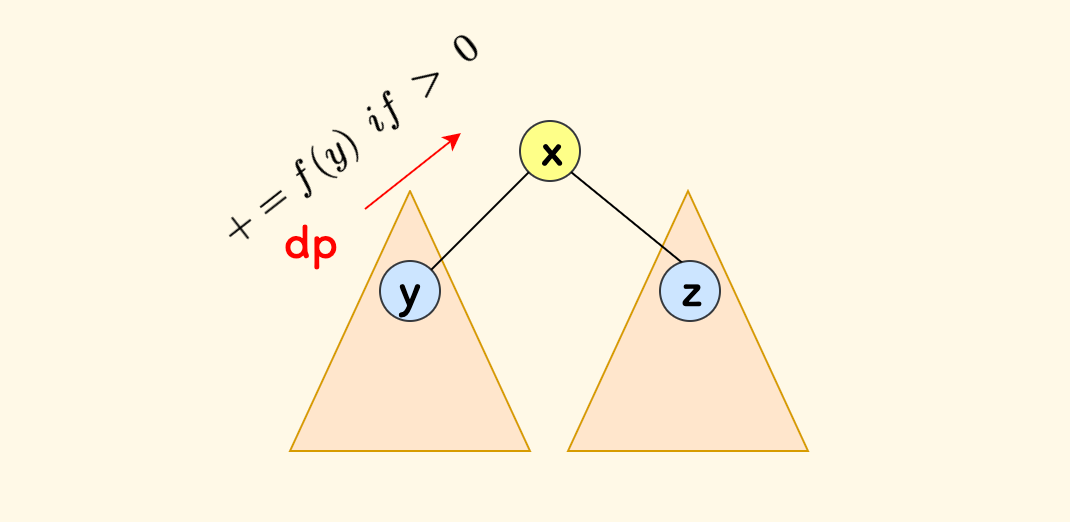
- 如果 $f(y)$ 是正数,那么就添加上子树 $y$ 的结果,这样 $x$ 子树内的结果会更大。
- 否则,$f(y)$ 是负数或者 $0$ 时,不选择子树 $y$。
总而言之:
\[f(x)\ += \begin{cases} f(y) &if\ f(y) > 0 \\ 0 & else \end{cases}\]至此,$f(1)$ 的结果是正确的。
但是,这只考虑了 $1$ 号作为根的情况。对于一个节点 $y$ 来说,缺失了从 $y$ 出发逆向到 $x$ 的情况, 也就是缺少了把 $y$ 当做根的情况。
因此,再进行第二次扫描,仍然从 $1$ 号节点出发,假定父节点 $x$ 的 DP 值已经修正,基于此,考虑进一步修正其子节点 $y$ 的 DP 值。
把子节点 $y$ 假设为新的树根,看下应该如何从已有的 DP 值增量推导出来其最终的 DP 值。
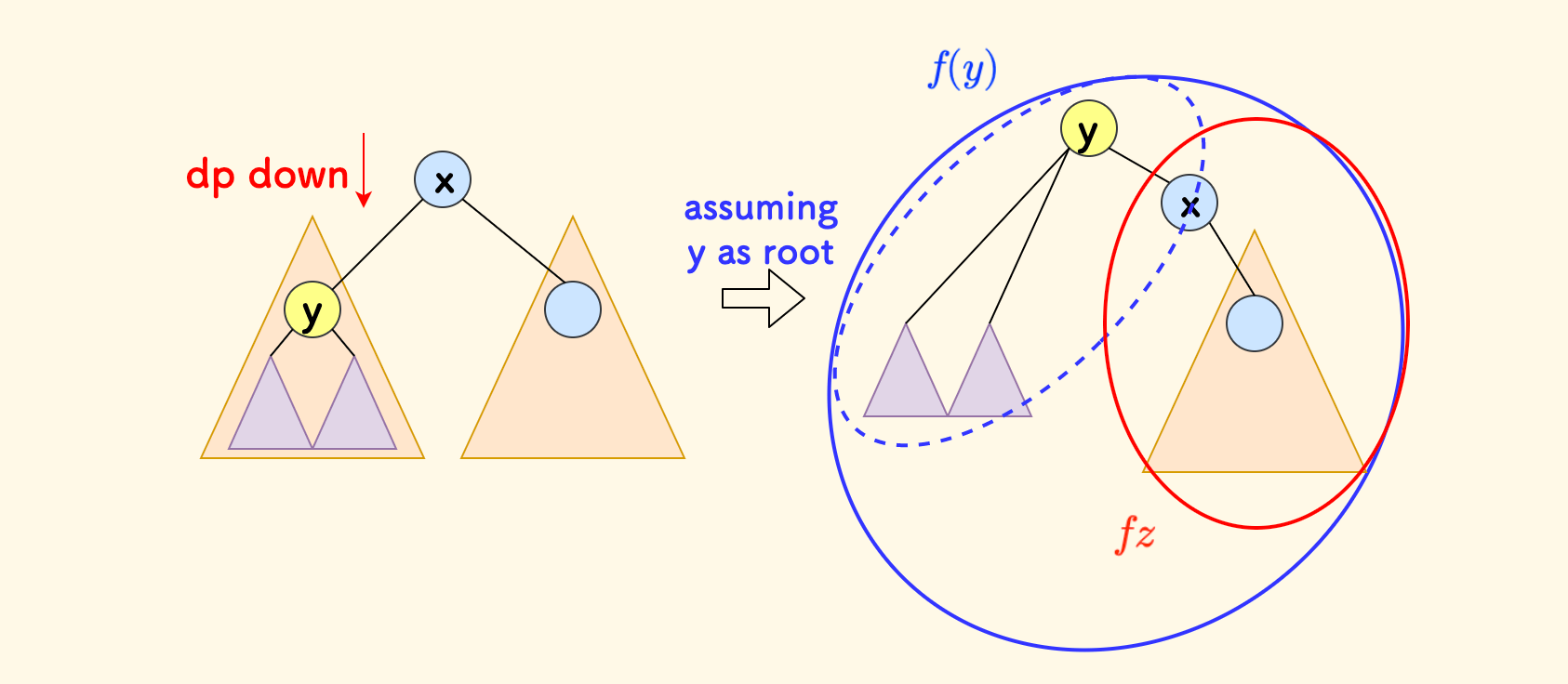
首先找出来原来的 $x$ 的子树中,除去 $y$ 的部分的贡献 $fz$,即图中红色圈中的区域。
如果 $f(y) > 0$,说明在第一次扫描过程中,$f(x)$ 一定包含进去了 $f(y)$,那么 $fz = f(x) - f(y)$。
否则,$f(x)$ 并未考虑进去 $f(y)$,此时 $fz = f(y)$。
然后,把 $y$ 当做新根的时候,$z$ 部分就成了 $y$ 的一颗子树。
同样地思考方式,只有当 $fz$ 是正数时,才有必要吸收其贡献。
用代码来表示这个修正过程:
int fz = f[y] > 0 ? (f[x] - f[y]) : f[x];
if (fz > 0) f[y] += fz;
由于 $1$ 号节点的 DP 值 $f(1)$ 在第一次扫描时已经是正确的,所以在第二次扫描时,从 $1$ 号节点不断考虑每个子节点,自上而下递推可以修正完所有节点的 DP 值。
C++ 代码实现如下:
最大白子树 - C++ 代码
const int N = 2 * 1e5 + 5;
int f[N];
int n; // 节点数
vector<vector<int>> edges; // 边 [x] => [y,z,...]
int ver[N]; // 节点权值,1 表示白色,-1 表示黑色
bool vis[N]; // 访问数组
void solve() {
memset(f, 0, sizeof f);
memset(vis, 0, sizeof vis);
function<void(int)> up = [&](int x) {
vis[x] = true;
f[x] = ver[x]; // 必选 x
for (auto y : edges[x]) {
if (vis[y]) continue;
up(y);
// 选or 不选子树 y
if (f[y] > 0) f[x] += f[y];
}
};
up(1);
memset(vis, 0, sizeof vis);
function<void(int)> down = [&](int x) {
vis[x] = true;
for (auto y : edges[x]) {
if (vis[y]) continue;
int fz = f[y] > 0 ? (f[x] - f[y]) : f[x];
if (fz > 0) f[y] += fz;
down(y);
}
};
down(1);
for (int x = 1; x <= n; x++) {
printf("%d ", f[x]);
}
putchar('\n');
}
最大深度和 ¶
给定一个 $n$ 个点的树,请求出一个节点,使得以这个节点为根时,所有节点的深度之和最大。
一个节点的深度定义为该节点到根的简单路径上边的数量。
节点标号的范围是 $1 \sim n$、各不相同,边的数量是 $n-1$。 求使得深度和最大的根节点。
-- 来自 洛谷 P3478. STA-Station
同样是一个不定根问题。
定义 $f(x)$ 为以节点 $x$ 为根时的整个树的总深度和。
选择 $1$ 号节点为根,进行第一次扫描,在递归的同时带上深度 $d$。
假设当前扫描的节点是 $x$,那么容易想到转移方程:
算上 $x$ 自身的深度:
\[f(x) = d\]依次遍历每个子节点 $y$,先递归计算子树的结果,然后计入 $f(x)$:
\[f(x)\ += f(y)\]
至此,$f(1)$ 的结果计算准确了。但是其他节点 $y$ 的 DP 值缺少到上游方向的情况。
此外,在第一次扫描时,可以同时计算一个子树的大小 $s(x)$,第二次扫描时修正 DP 时会用到。
最大深度和 - 第一次扫描 - C++ 代码
function<void(int, int)> up = [&](int x, int d) {
vis[x] = true;
f[x] = d; // 加上节点 x 自身的深度
for (auto y : edges[x]) {
if (vis[y]) continue;
up(y, d + 1);
f[x] += f[y]; // 加上子树 y 的深度和
s[x] += s[y]; // s[x] 是子树的大小
}
};
up(1, 0); // 初始深度 d=0
第二次扫描时,在父节点 $x$ 的 DP 值已经正确的前提下,增量修正其子节点 $y$ 的 DP 值。
下图中,原来以 $x$ 为根的情况,子树 $y$ 的部分叫做 Y(图中蓝色圈), 整个树其余部分叫做 Z(图中红色圈)。
现在考虑以 $y$ 为新根的情况,相对于以 $x$ 为根的情况,总的深度和发生了哪些增量变化。
- 蓝色的
Y上升了一个高度,也就是其中每个节点深度减 $1$,总和则减少了 $s(y)$。 红色的
Z下降了一个高度,也就是其中每个节点深度加 $1$,总和则增加了 $s(Z)$。而 $Z$ 部分的大小是 $s(1) - s(y)$。
所以最终修正 DP 的方程是:
\[f(y) = f(x) - s(y) + s(1) - s(y)\]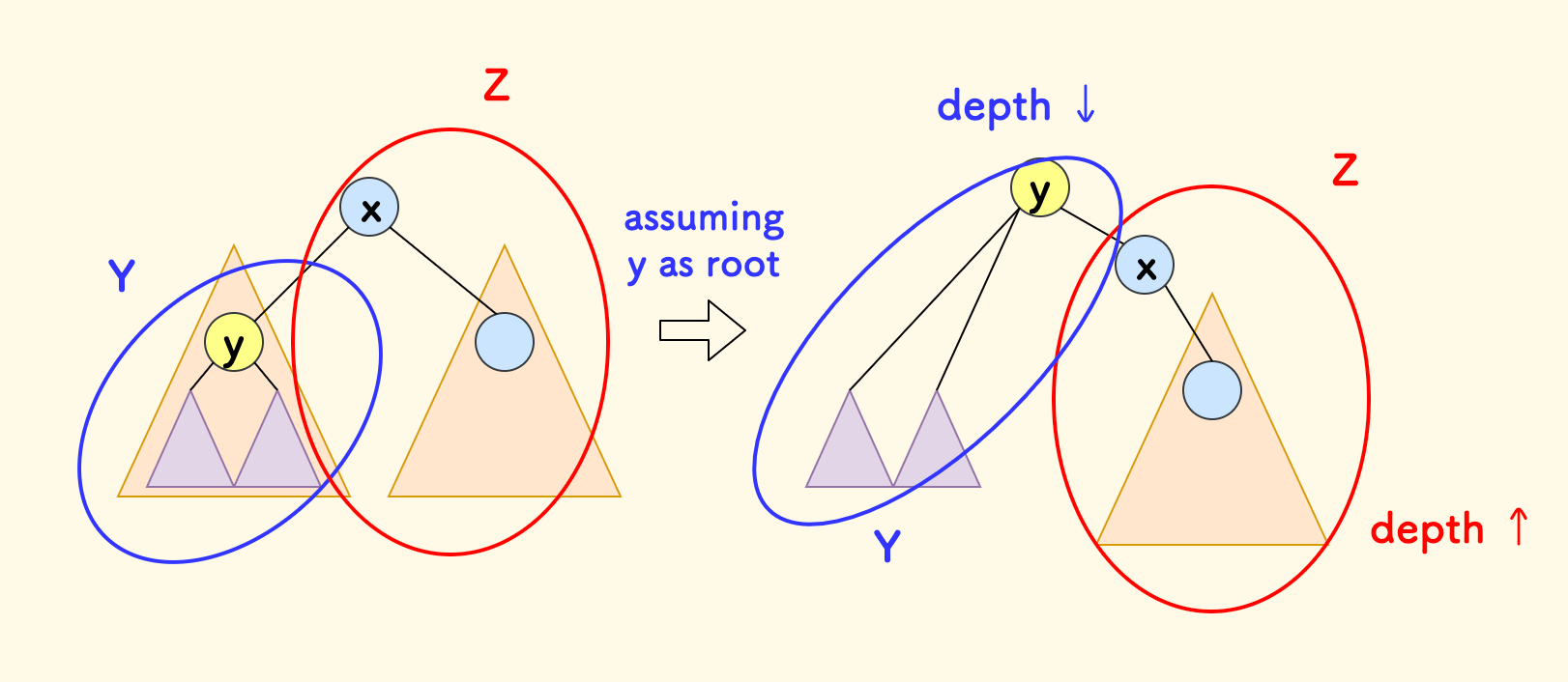
最大深度和 - 第二次扫描 - C++ 代码
memset(vis, 0, sizeof vis);
function<void(int)> down = [&](int x) {
vis[x] = true;
for (auto y : edges[x]) {
if (vis[y]) continue;
f[y] = max(f[y], f[x] - s[y] + s[1] - s[y]);
down(y);
}
};
down(1);
最终,遍历 $f$ 数组,取出使得 $f$ 值最大的那个节点返回即可。
统计可能的树根 ¶
现有一颗含有 $n$ 个节点、$n-1$ 条边的树、节点号是 $0 \sim n-1$。 所有的边由数组 $edges$ 给出,其中 $edges_i$ 是 $(u_i, v_i)$ 表示节点 $u_i$ 和 $v_i$ 之间有一条无向边。
给你一个数组 $guesses$,其中每一项是只有两个不同大小的元素的数组 $(u, v)$,表示 $u$ 是 $v$ 的父节点。
考虑每个节点 $x$ 作为根的时候,子树中有多少个边 $(u, v)$ 在这个 $guesses$ 数组中存在,假设这个数值是 $f(x)$。
给定一个整数 $k$,输出所有不小于 $k$ 的 $f(x)$ 的节点个数。
-- 来自 leetcode 2581. 统计可能的树根数目
同样是一个不定根问题。
先预处理一下,以便快速访问,略去说明。
统计可能的树根 - 预处理 - C++ 代码
// 预处理边
int n = edges.size() + 1;
vector<vector<int>> ed(n);
for (auto& e : edges) {
ed[e[0]].push_back(e[1]);
ed[e[1]].push_back(e[0]);
}
// 预处理猜测 g[father] -> child
vector<unordered_set<int>> g(n);
for (auto& gs : guesses) {
g[gs[0]].insert(gs[1]);
}
同题目中一样,定义 $f(x)$ 是以节点 $x$ 为根时命中的边的数目。最终我们要统计所有满足 $f(x) \geq k$ 的节点数量。
以 $0$ 号节点为根,先进行第一次扫描,假设现在扫描的节点是 $x$,那么:
- 先递归计算完每个子树 $y$,并计入贡献 $f(x) += f(y)$。
- 如果边 $(x, y)$ 命中,则计入 $f(x) += 1$。
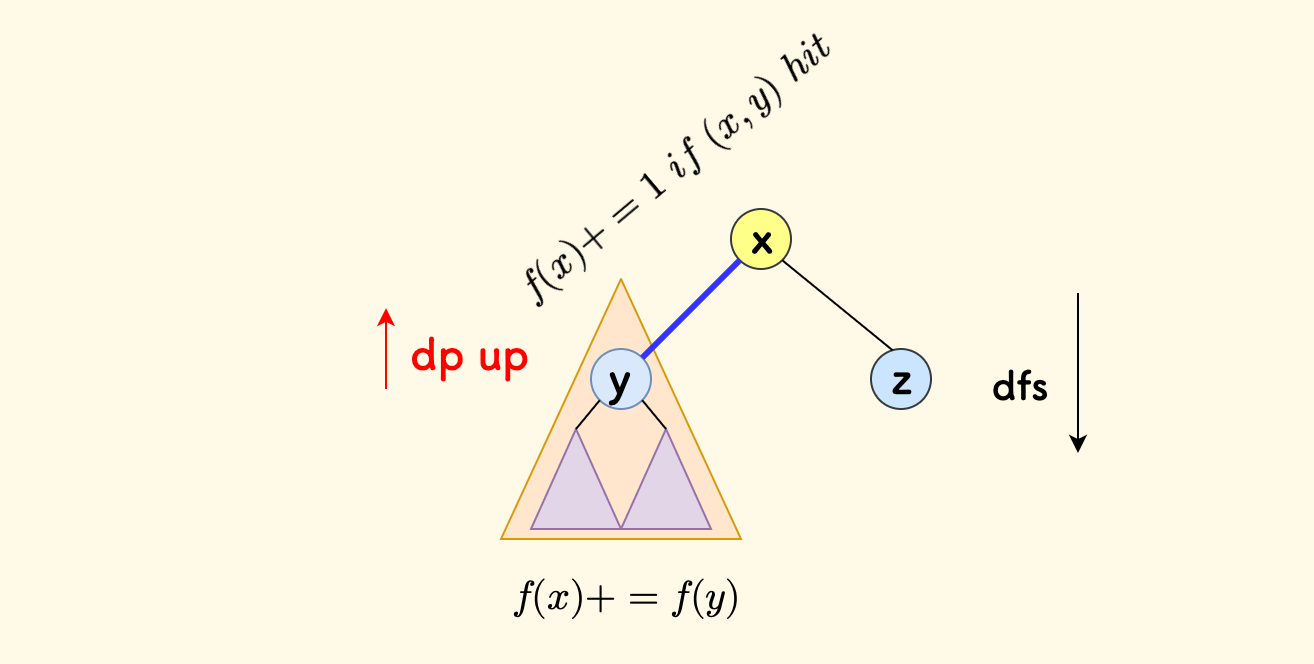
至此,$f(0)$ 的结果已计算准确,但是其他节点 $y$ 缺少逆方向的答案计算。
统计可能的树根 - 第一次扫描 - C++ 代码
vector<int> f(n, 0);
vector<bool> vis(n, false);
function<void(int)> up = [&](int x) {
vis[x] = true;
for (auto y : ed[x]) {
if (vis[y]) continue;
up(y);
f[x] += f[y];
// (x, y) 是否是命中
if (g[x].find(y) != g[x].end()) ++f[x];
}
};
up(0);
第二次扫描时,仍然从 $0$ 号节点出发,假定父节点 $x$ 的 DP 值已经正确,逐步修正每个子节点 $y$ 的 DP 值。
如下图中,假设在以 $x$ 为根的时候,$y$ 节点的子树部分是 Y (蓝色圈),树的其它部分是 Z(红色圈)。
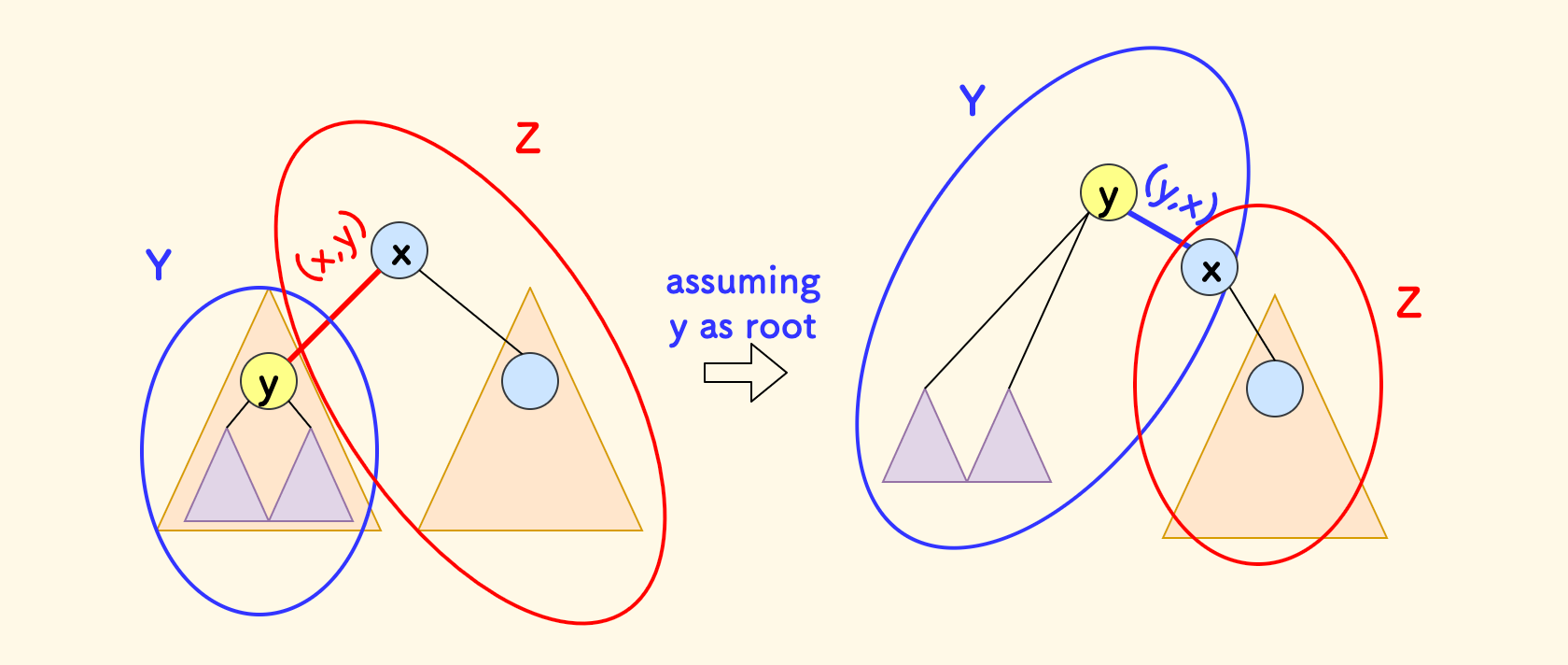
那么现在,考虑把 $y$ 设为新的树根的情况,看看前后发生了什么变化:
Z是否应该舍弃边 $(x,y)$ ?原来的情况下,
Z部分的贡献是 $z=f(x)-f(y)$。考虑 $y$ 成为新根后,如果边 $(x,y)$ 原来命中了
guesses数组,现在边的方向变了,要剔除其贡献:$z-=1$。然后 $z$ 计入 $f(y)$ 。
Y是否应该加入边 $(y,x)$ ?边 $(x,y)$ 反向后成了 $(y,x)$,要考虑它是否命中,如果命中的话,则计入 $f(y) += 1$
代码实现如下:
统计可能的树根 - 第二次扫描 - C++ 代码
fill(vis.begin(), vis.end(), false);
function<void(int)> down = [&](int x) {
vis[x] = true;
for (auto y : ed[x]) {
if (vis[y]) continue;
// Z 是否应该撤销边 (x,y) ?
int z = f[x] - f[y];
if (g[x].find(y) != g[x].end()) --z;
f[y] += z;
// Y 是否应该新增边 (y,x) ?
if (g[y].find(x) != g[y].end()) ++f[y];
down(y);
}
};
down(0);
最终统计一下不小于 $k$ 的 $f$ 的节点个数即可。
统计素数路径 ¶
给定一颗含有 $n$ 个节点的无向树,节点标号 $1 \sim n$。 输入一个长度为 $n-1$ 的数组 $edges$,其中 $edges_i$ 是 $(u_i, v_i)$ 表示节点 $u_i$ 和 $v_i$ 之间有一条无向边。
树中的合法路径定义为:不同的两个节点之间恰好只包含一个素数的路径。
路径 $(u, v)$ 和 $(v, u)$ 算作同一条路径,计算一次。
请你返回树中的合法路径数目。
-- 来自 2867. 统计树中的合法路径数目
可以看出,这是一个不定根问题,树中的边是无向的。
首先,预处理一下边,以便快速访问,详略。
统计树中的合法路径数目 - 预处理边 - C++ 代码
// 预处理边 (存图)
vector<vector<int>> ed(n + 1);
for (auto& e : edges) {
ed[e[0]].push_back(e[1]);
ed[e[1]].push_back(e[0]);
}
然后,提前算出来不超过 $n$ 的素数表 pt,可以用 埃氏筛 来做,详略。
预处理后,如果 pt[x] 是 true,则表示数字 x 是一个素数。
统计树中的合法路径数目 - 埃氏筛预处理素数表 - C++ 代码
// 预处理素数表 埃氏筛
vector<bool> pt(n + 1, true);
pt[0] = pt[1] = false;
for (int i = 2; i * i <= n; i++) {
if (!pt[i]) continue;
for (int j = i * i; j <= n; j += i) pt[j] = false;
}
一条合法路径恰好只包含一个素数,那么可以按素数节点来计算路径数目。
对于一个素数节点 $x$ 来说,考虑所有连通到此节点的只包含合数的路径,即可形成合法的素数路径。
下图的例子中,假设连通节点 $x$ 的三颗子树,经过一个合数节点到达 $x$ 的路径数目分别是 $a$,$b$ 和 $c$ 。
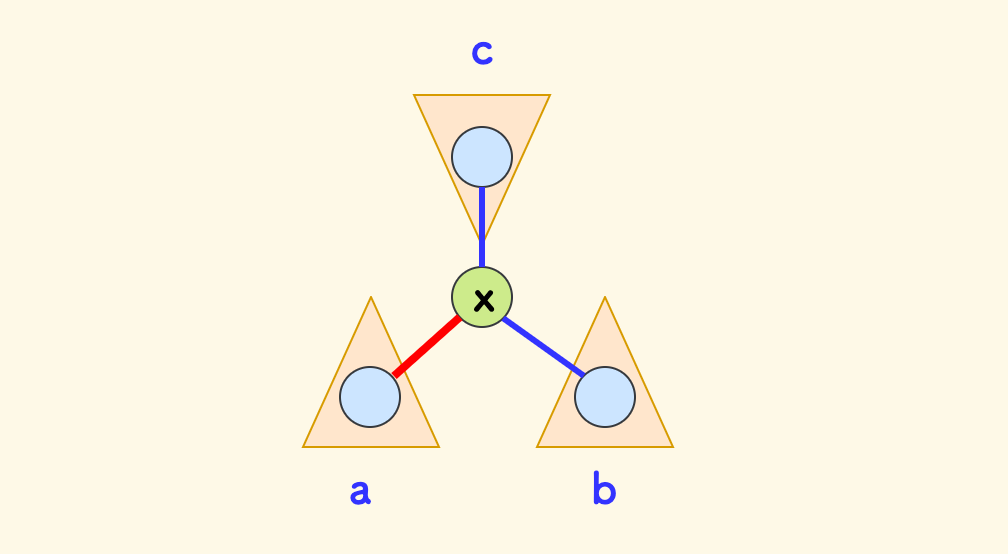
那么可形成的合法路径的数目是:
- 以 $x$ 为端点的路径(图中红色的是一个例子),共 $a+b+c$ 条。
- 穿过 $x$ 的路径(图中蓝色的是一个例子),共 $ab + bc + ac$ 条。
那么得到了以下结论:
- 可以先计算只包含合数的路径。
- 对每个素数节点,结合到达它的合数路径,可以计算出包含此素数节点的答案。
但是这个 $ab+bc+ac$ 怎么计算呢?看起来要两层循环,但是其实可以用前缀和技巧来优化。
\[\begin{split} ab + bc + ac &= 0 \times a \\ &+ (0 + a) \times b \\ &+ (0 + a + b) \times c \end{split}\]定义 $f(x)$ 为子树 $x$ 以节点 $x$ 为端点的只含合数的路径 (只包含 1 个节点也行)。
那么对于每个素数节点 $x$,考虑其连通的子节点 $y$ 的话,根据上面的结论,包含这个素数节点的素数路径数目,可以用下面的代码来计算:
ll ans = 0; // 最终答案
// f[y] 的前缀和, 计算以 x 为端点的合法路径
int s = 0;
// q 是 f1*f2 + f1*f3 + f2*f3 ..., 计算穿过 x 为端点的合法路径
ll q = 0;
for (auto y : ed[x]) { // 遍历每个可以连通 x 的节点 y
q += s * f[y];
s += f[y];
}
ans += q + s; // q+s 就是所有包含素数 x 的合法路径
所以,如果推导出 $f(x)$ 来,那么对所有素数节点可以在 $O(n)$ 内推导出其答案(边的总数不超过 $n$ 的)。
下面即可专注求解 $f(x)$,同样是一个换根 DP。
首先,对所有合数初始化 $f(x)$ 到 $1$,因为允许单节点的合数路径。
统计树中的合法路径数目 - 预处理 $f$ 数组 - C++ 代码
vector<int> f(n + 1, 0);
for (int x = 1; x <= n; x++)
if (!pt[x]) f[x] = 1;
先以 $1$ 号节点为根,向下 DFS 进行第一次扫描。假设现在扫描的节点是 $x$, 如果它是一个合数,那么需要先递归计算其每个子树 $y$,然后贡献给 $x$ 即可。
这一步比较容易想到:
统计树中的合法路径数目 - 第一次扫描 - C++ 代码
// 后序计算 pushup
vector<bool> visit(n + 1, false);
function<void(int)> up = [&](int x) {
visit[x] = true;
for (auto y : ed[x]) {
if (visit[y]) continue;
up(y);
// 以 x 为端点的合数路径
if (!pt[x]) f[x] += f[y];
}
};
up(1);
经过第一次扫描,只考虑了以 $1$ 为根的情况,也就是说 $f(1)$ 是正确的。但是其他节点 $f(y)$ 缺少了逆向路径的考虑。
仍然从 $1$ 号节点出发,向下 DFS 进行第二次扫描,假定父节点 $x$ 的 DP 值已经正确求出,进一步修正其各个子节点 $y$ 的 DP 值。
考虑把 $y$ 设置为新的树根,观察相比原来的第一次扫描 $f(y)$ 有何变化。
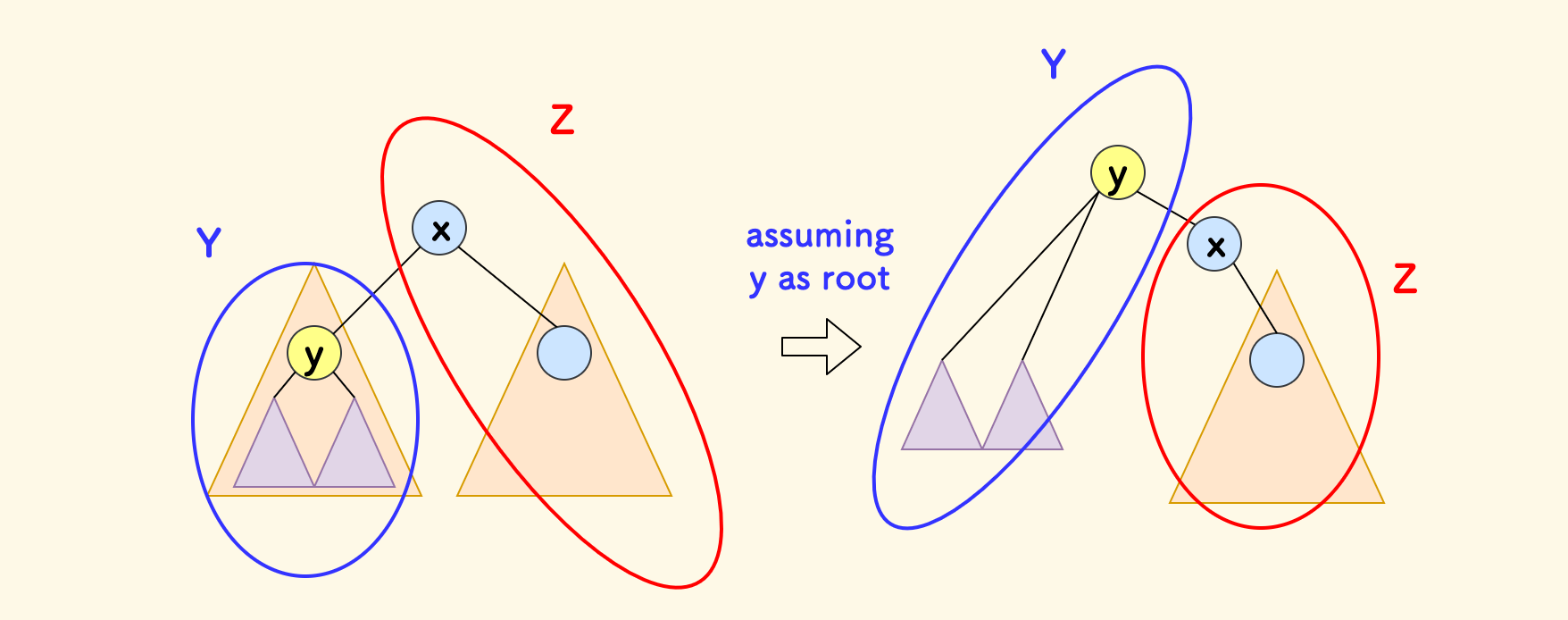
如图所示,在第一次扫描时,假设 Y 的子树是蓝色圈的部分,整个树其余的部分是红色的 Z。
- 如果 $x$ 是一个素数,那么在 $y$ 为新根的情况下,
Y不应该吸收Z的贡献,而且此时Z部分的 $f$ 值肯定也是 $0$。 - 如果 $x$ 是一个合数,那么在 $y$ 为新根的情况下,
Y需要吸收Z的贡献。而Z的 $f$ 值即 $f(x) - f(y)$。
当然,只有在 $y$ 是合数的情况下,才需要计算 $f(y)$。
用代码来表示的话,会很简洁:
// 来自 x 的以 y 为端点的合数路径, 注意减去自己原本的贡献
if (!pt[y] && !pt[x]) f[y] += f[x] - f[y];
第二次扫描的代码如下:
统计树中的合法路径数目 - 第二次扫描 - C++ 代码
// 前序计算
fill(visit.begin(), visit.end(), false); // 复用下 visit 数组
function<void(int)> down = [&](int x) {
visit[x] = true;
for (auto y : ed[x]) {
if (visit[y]) continue;
// 来自 x 的以 y 为端点的合数路径, 注意减去自己原本的贡献
if (!pt[y] && !pt[x]) f[y] += f[x] - f[y];
down(y);
}
};
down(1);
最终,统计每个素数的答案,求和即可,代码略。
简单总结 ¶
- 不定根是换根法的关键暗示。
- DP 程式要可以增量修正。
- 第一次扫描自下而上转移、第二次扫描自上而下转移(修正 dp )。
- 换根时注意剔除新根原来作为子节点对父节点的贡献。
(完)
本文参考书:《算法竞赛进阶指南》· 李煜东
相关阅读: 最小高度树(拓扑 & 换根)



