逆序对计数问题是一个经典算法问题,一般有两种解法,本文是基于归并排序的方法, 另一种是 基于「树状数组」的解法。
问题描述:
对于给定的一段正整数序列
a,逆序对就是序列中满足a[i] > a[j]且i < j的数对,求数列中所有的这种数对的数量。-- 来自 洛谷 P1908, leetcode 类似问题 《交易逆序对的总数》
前置知识点:归并排序。
理解了归并排序过程,就很容易想到怎么解了,只需要一张图来说明:
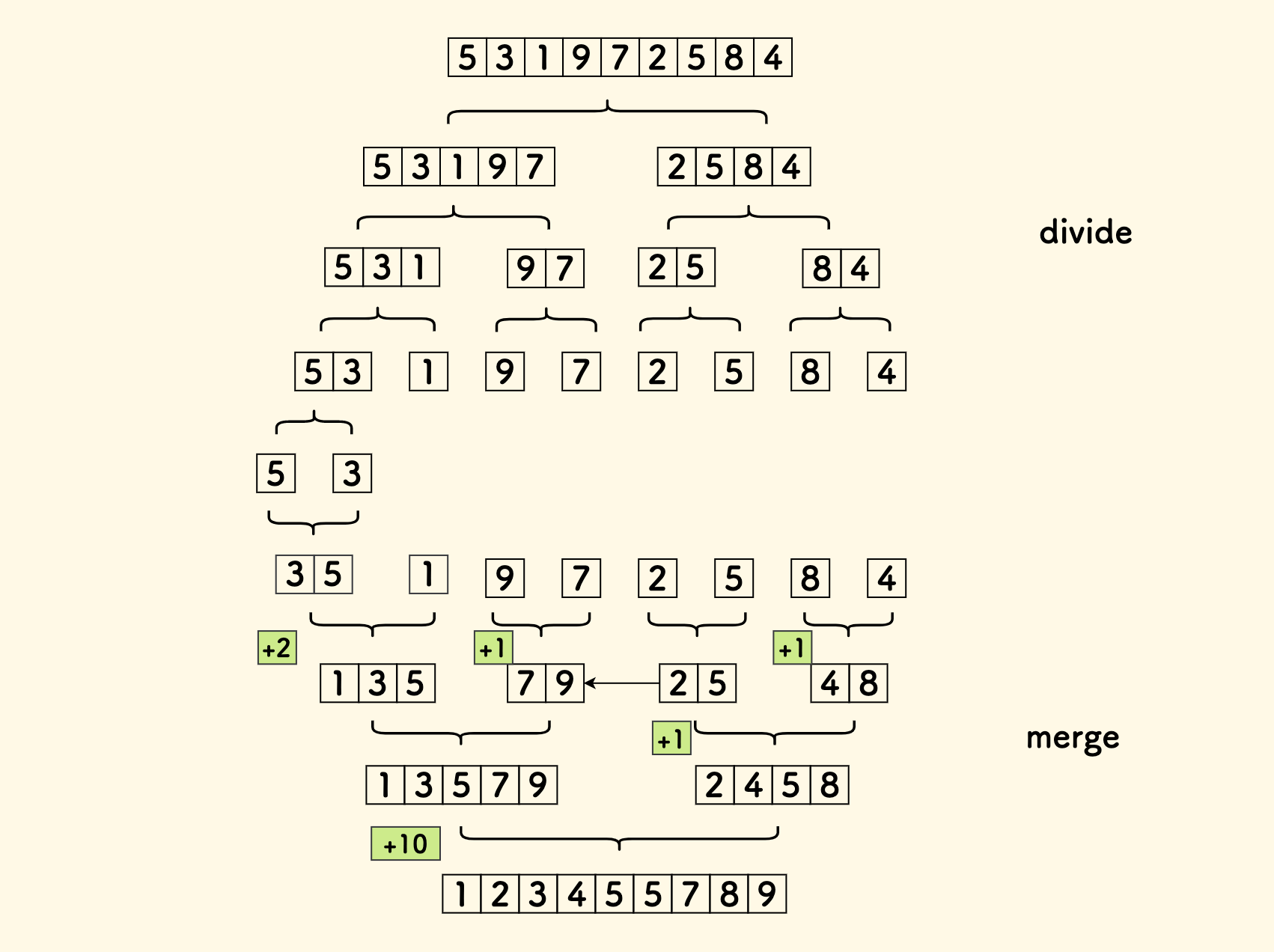
其实就是在合并过程中,进行计数。
只需要改造归并排序的子函数,伪代码如下:
// 合并两个有序数组 a 和 b 到 c
// [start1, end1] 是 a 的要合并的区间
// [start2, end2] 是 b 的要合并的区间
// start 是 c 数组的合并目标起始位置
int Merge(int a[], int start1, int end1, int b[],
int start2, int end2, int c[], int start) {
int ans = 0;
while (start1 <= end1 && start2 <= end2) {
if (a[start1] <= b[start2])
c[start++] = a[start1++];
else {
c[start++] = b[start2++];
// 逆序对计数
ans += end1 - start1 + 1;
}
}
while (start1 <= end1) c[start++] = a[start1++];
while (start2 <= end2) c[start++] = b[start2++];
return ans;
}
总的代码实现见:
(完)
相关阅读:
本文原始链接地址: https://writings.sh/post/reverse-order-pairs-merge-sort
