树状数组的原理、结构和典型应用

树状数组是一种将区间信息树状化的数据结构。

它可以 $\log{n}$ 时间复杂度动态地维护区间和、区间最值。代码简短优雅，典型应用于逆序对计数、1D 动态规划转移优化等。

树状数组的原理和结构 ¶

先看一个模板题：

已知一个数列，你需要进行下面两种操作：
将某一个数加上一个数字
求出某区间每一个数的和
输入包含多组「单点增加」和「区间查询」的操作。
-- 洛谷 P3374 树状数组模板题

这个问题要求动态地支持「单点增加」和「区间求和」。

朴素的方法，一个数组的单点修改时间复杂度是 $O(1)$，区间求和是 $O(n)$。

前缀和方法，区间求和的时间复杂度是 $O(1)$，而单点修改会影响后续所有的前缀和，时间复杂度是 $O(n)$。

这两种传统方法的问题在于，两种操作都存在的情况下，瓶颈仍然是 $O(n)$。

树状数组是一种折中的方法，两种操作都可以做到 $O(\log{n})$，虽然每种操作都不是最快，但是降低了两种操作的时间复杂度瓶颈。

lowbit 函数和区间拆分

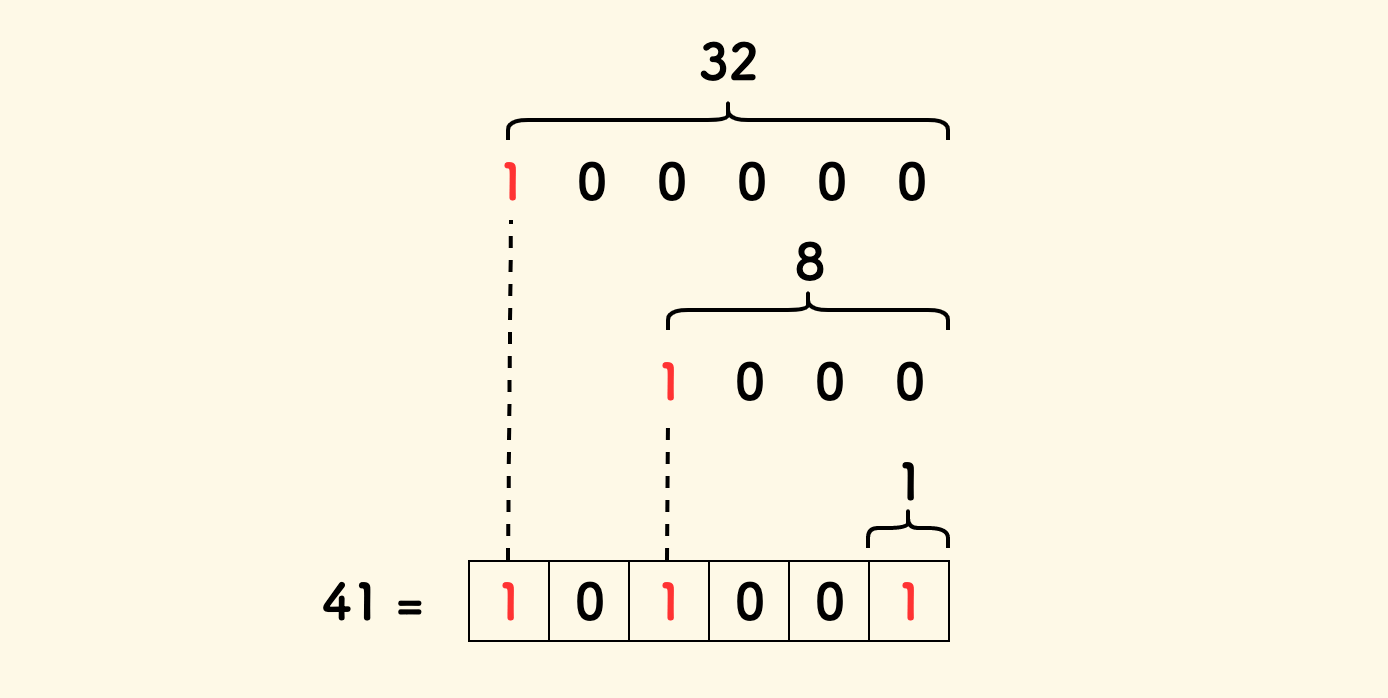
任何一个正整数 x 都可以拆成二进制求和的形式：

x = 41 = 0b101001
       =  32      +     8    +        1
       = 0b100000 + 0b001000 + 0b000001  // 二进制

那么区间 [1,41] 也可以如此拆分为长度分别为 32、8 和 1 的三个小区间：

[1, 41] => [1,  32]    // 长度为 32 = 0b100000
        +  [33, 40]    // 长度为 8  = 0b001000
        +  [41, 41]    // 长度为 1  = 0b000001

拆成多少个小区间，取决于 x 的二进制表示下有多少个 1。

而每个小区间的长度，就是相应位上的 1 和后面所有位变为 0 后形成的数。

lowbit 函数可以用来取一个整数在二进制下最低位的 1 和后面的 0 形成的数。

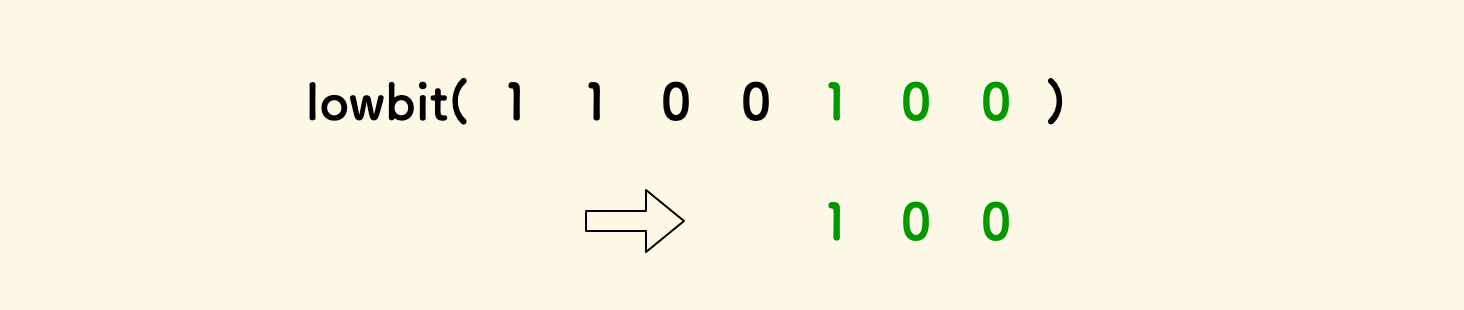
lowbit 函数的实现非常简单：

int lowbit(int x) { return x & -x; }

所有的小区间的长度，可以不断执行 lowbit 函数来得到。

这样原区间 [1,x] 可以拆成 log(x) 个小区间。每个小区间的右端点是 x 的话，长度就是 lowbit(x)：

while (x) {
    // 当前小区间的右端点是 x
    // 当前小区间的长度是 lowbit(x)
    // 然后减去它，继续
    x -= lowbit(x);
}

树状结构

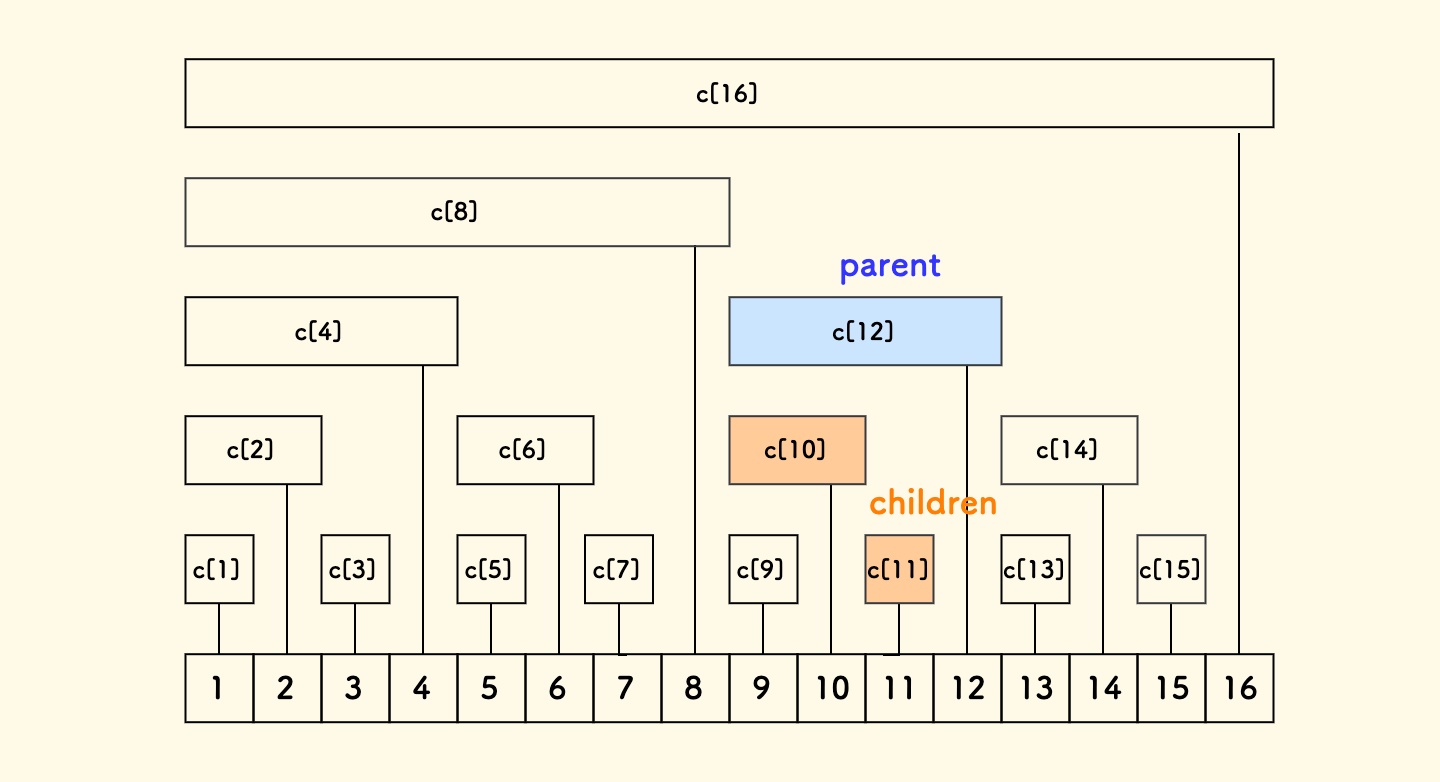
定义一个数组 c，其中 c[x] 维护原数组 a[x] 在区间 [x-lowbit(x)+1, x] 上的和。

简而言之，每个 c[x] 代表了一个以 x 为右端点的小区间。

可以将树状数组理解为下图的样子，c[x] 只负责右端点是 x 的小区间的和。

如果一个小区间完全覆盖另一个小区间，那么前者可以称为后者的祖先。最近的祖先就是父节点。

这个结构有下面的性质：

父节点 c[x] 保存其所有子孙节点的总和。
节点 c[x] 的父节点是 c[x+lowbit(x)] (说明见图下方)。
上面一层管辖的区间是当前层的二倍长。
x 为 2 的幂数时，比如 c[2^k] 时，会管辖整个前缀区间（因为其 lowbit 是自身）。

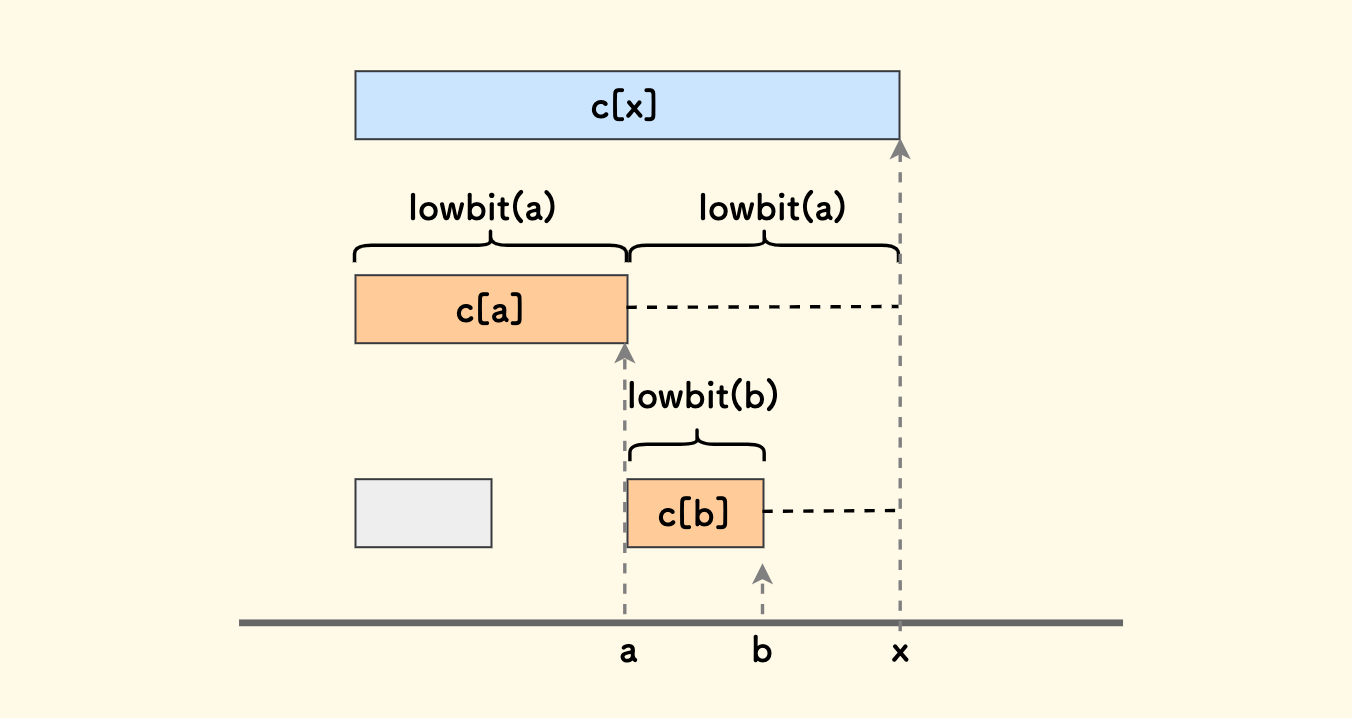
c[x] 的父节点的是 c[x+lowbit(x)] 的说明

比如说，c[x] 的前两个子节点分别是 c[a] 和 c[b]，我们知道它们管辖的区间长度分别是 lowbit(a) 和 lowbit(b)。

而且知道，任何一个小区间 c[x] 的右端点是 x。

第一个子节点 c[a] 一定是二分父节点的区间的，所以 x = a + lowbit(a)。

同样，第二个子节点 c[b] 一定是二分剩下的区间的，所以 x = b + lowbit(b)。

依次类推，所有节点的父节点具可以据此规律来求。

区间求和

以 x=15 为例，那么区间 [1,15] 上的求和过程：

sum[1, 15] = sum[15, 15] + sum[13, 14] + sum[9, 12] + sum[1, 8]
            = c[15]      + c[14]       + c[12]      + c[8]

在图上就表现为一个从右向左的爬树相加过程。

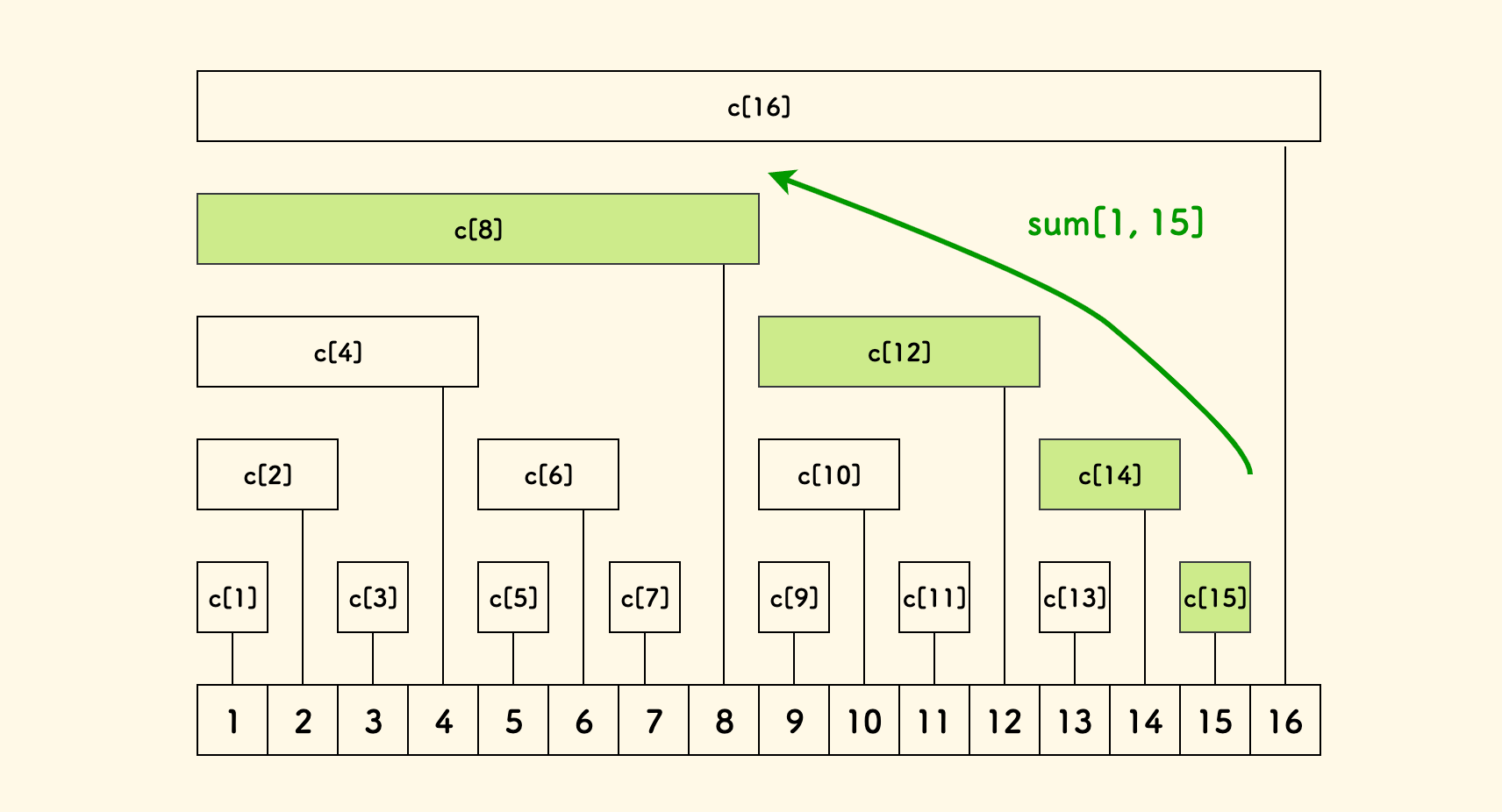
可以从图中观察到：求和过程一定终止于最近的那个 2 的幂数 c[2^k] 上，因为它管辖整个前缀区间。

可以写出树状数组上的前缀区间的求和代码：

int c[n+1];

// 查询区间 [1, x] 上的和
int ask(int x) {
    int ans = 0;
    for (; x; x -= lowbit(x)) ans += c[x];
    return ans;
}

如果要查询非前缀区间 [a, b] 上的和，由于算术加法可以用减法作为逆操作，可以直接：

// sum[a, b] ← sum[1, b] - sum[1, a-1]
void query(int a, int b) { return ask(b) - ask(a-1); }

单点增加

现在考虑单点增加操作。

以增加 a[5] 为例，比如说 a[5] += d，它会影响所有后面的前缀区间 [1, x>=5] 的和。

但是，包含 a[5] 这个成分的小区间，只有其祖先。

包含单点 a[5] 最小的区间是 [5,5]，然后找它的祖先区间：

x              => c[5]     // 小区间 [5,5]
x += lowbit(5) => c[6]     // 小区间 [5,6]
x += lowbit(6) => c[8]     // 小区间 [1,8]
x += lowbit(8) => c[16]    // 小区间 [1,16]

不断 lowbit 函数加上去，找出其所有祖先：

while (x <= n) {
    // x + lowbit(x) 后是父节点管辖区间的右端点
    x += lowbit(x);
}

单点增加 a[5] += d，就要把 c[5] 的所有祖先区间都加上 d，下图中可以看到，这其实是一种自左向右的爬树过程。

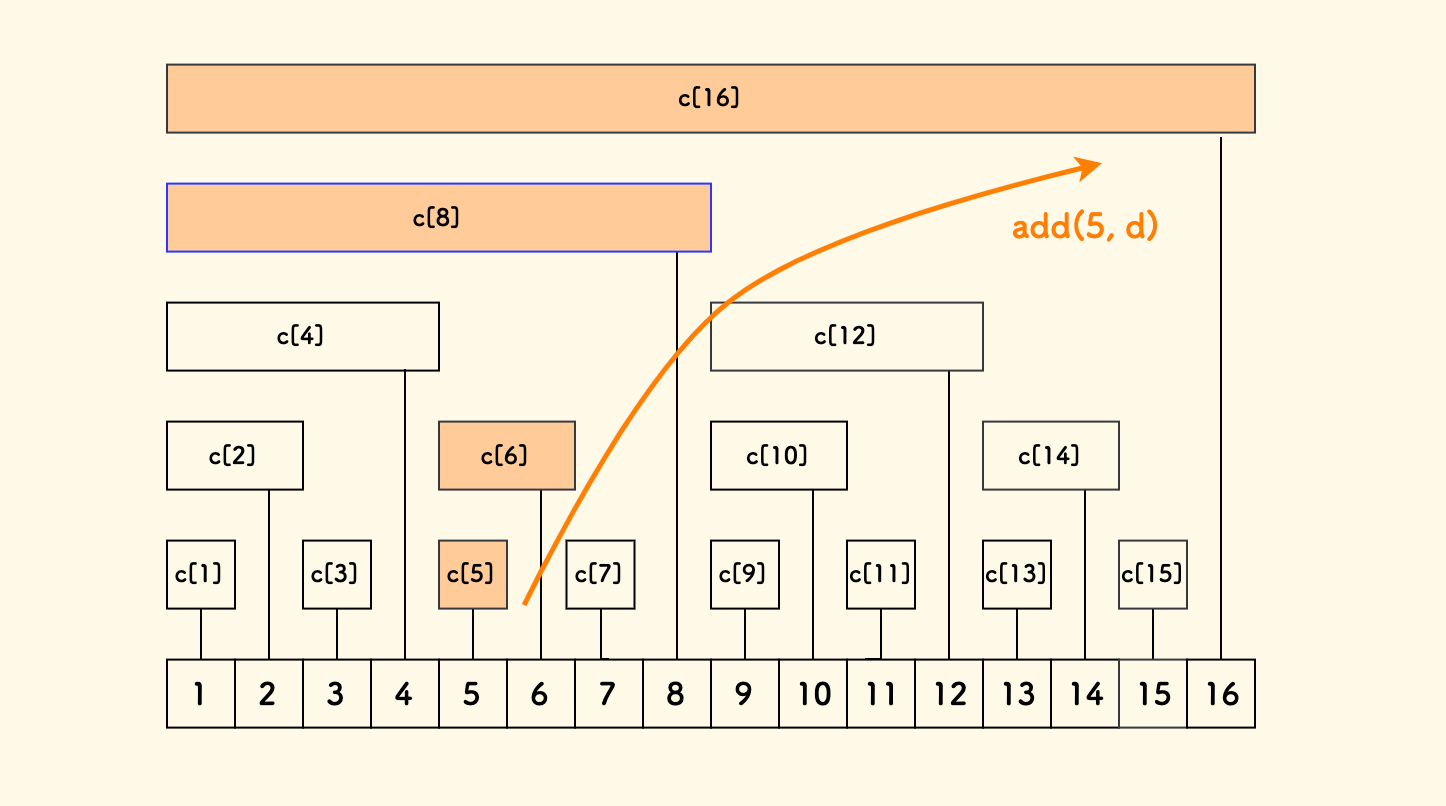
其实，也可以验证下，当操作完 a[5] 的单点增加操作后，会引起 c[8] 的维护。而前面查询区间 [1, 15] 的前缀和，会恰好路过 c[8]。

单点增加的代码如下：

void add(int x, int d) {
    for (; x <= n; x += lowbit(x)) c[x] += d;
}

如果要支持赋值操作，可以转化到「增加」：

void set(int x, int val) { return add(x, val - x); }

树状数组的所有代码就这两个函数，非常简短，时间复杂度都是 $\log{n}$，其中 $n$ 是原数组的总区间的大小。实现细节上，要注意的是，树状数组的第 0 个元素，是不使用的，所以申请的空间大小是 n+1。

回味一下，树状数组的本质，就是把区间和拆分到多个不同层次的小区间上去维护，以平衡单点修改和区间查询的时间复杂度。

维护区间最值 ¶

动态维护区间和是树状数组最基本的应用。

树状数组还可以维护单点修改情况下的区间最值，不过情况稍复杂一点。

以求最大值为例，区间拆分和之前是完全一样的。定义数组 c[x] 维护原数组 a[x] 在区间 [x-lowbit(x)+1, x] 上的最大值。

容易写出和前面类似的实现：

树状数组维护前缀区间上的最大值 C++ 实现

int c[n+1];

// 查询区间 [1, x] 上的最大值
int ask(int x) {
    int ans = 0;
    for (; x; x -= lowbit(x)) ans = max(ans, c[x]);
    return ans;
}

// 更新 a[x] = v 后，维护树状数组
void update(int x, int v) {
    for (; x <= n; x += lowbit(x)) c[x] = max(c[x], v);
}

但是，这仅仅适合于前缀区间。

如果要查询非前缀区间 [l,r] 上的最大值呢？求和运算可以用两个前缀区间的和相减来达到目的，但是最值操作并没有逆运算。

比如说，求区间 [5,15] 上的最大值，可以拆分为几个小区间：

max[5, 15] = max(
                max[15, 15],  // c[15]
                max[13, 14],  // c[14]
                max[9, 12],   // c[12]
                max[5, 8],    // ?
            )

前面几个区间都是和以前一样、形如 [x-lowbit(x)+1, x] 的小区间。但是最后这个区间 [5, 8] 并不是一个完整的小区间，没有办法利用 c[x] 数组存储的信息。

好像只能依次枚举。

下面的示意图中，求解区间 [5,15] 上的最大值，一开始可以走自右向左的爬树过程，跳着走。但是，最后余下的一小段区间（蓝色框中部分），只好依次枚举。

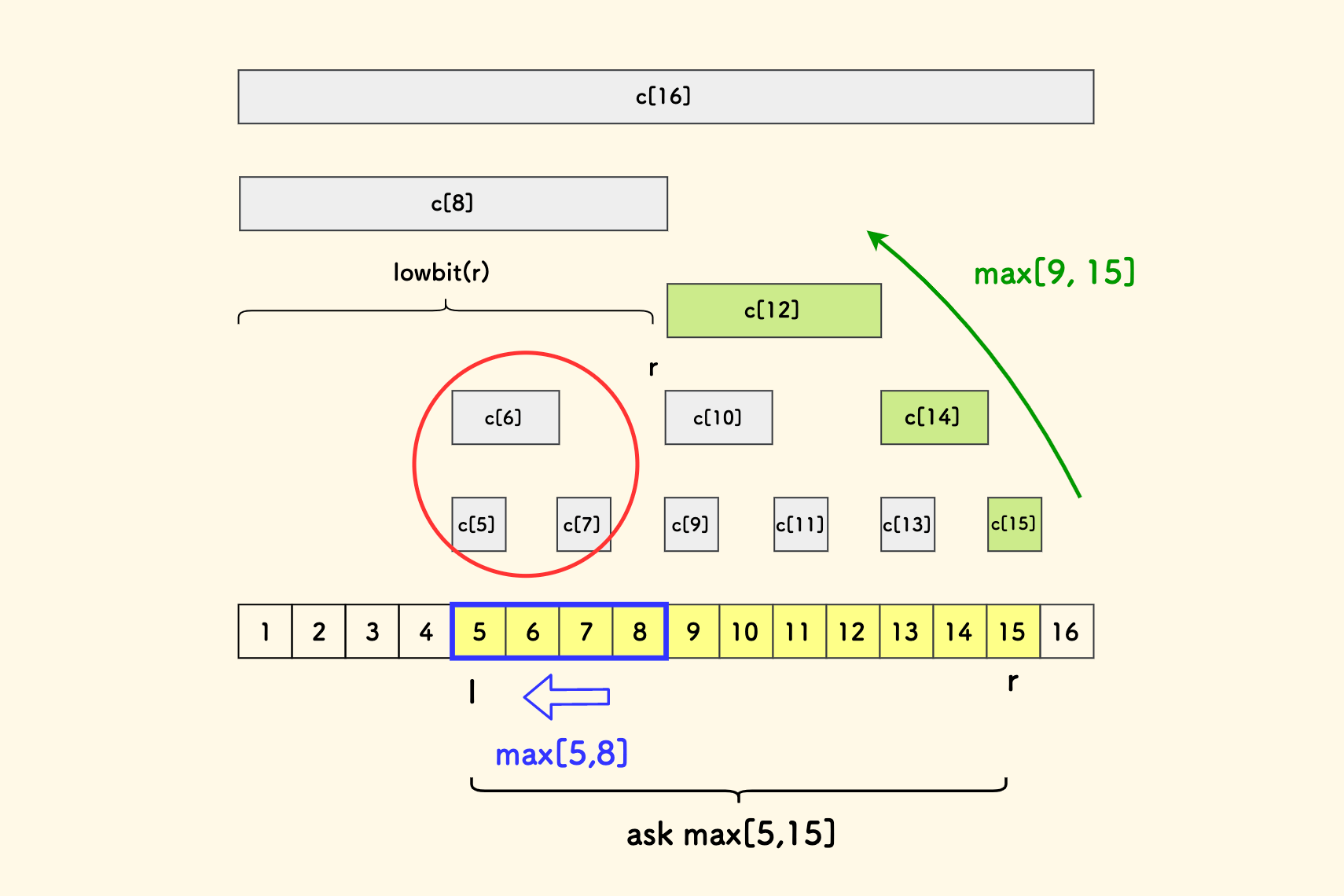
但是，注意到左边红色圈中的这些小区间，完全没有利用上。换句话说，还可以优化。

当无法继续「跳着走」时，可以尝试活动一下 r，比如当小区间接触到图中的蓝色框部分时，直接检查下 a[r]，然后 r-- 移动一步。

可以看到，稍微活动一下，有机会找到新的「跳着走」的路子，性能会更优：

max[5, 15] = max(
                max[15, 15],  // c[15]
                max[13, 14],  // c[14]
                max[9, 12],   // c[12]
                a[8],
                max[7, 7],    // c[7]
                max[5, 6],    // c[6]
            )

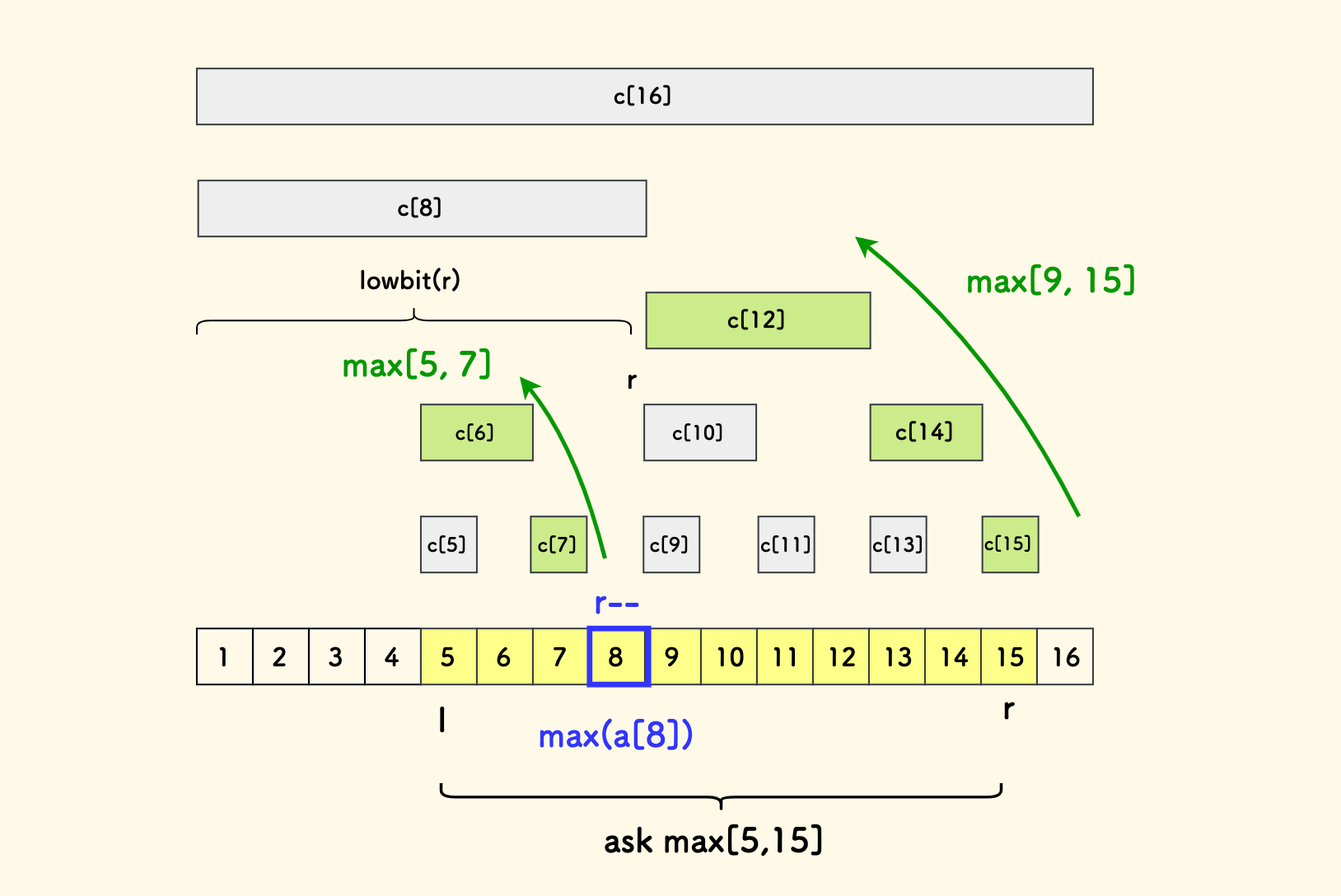
那总体简单地说，如何查询 max[l, r] 的思路就是：

尝试跳着走，直到小区间的左端点抵达左边界 l。
如果无法跳着走，尝试枚举一次，再次尝试跳着走。

用代码来表示这个过程：

树状数组查询区间最值 - C++ 实现

// 查询 [l..r] 区间维护的最大值
int ask(int l, int r) {
    // 从 r 向前枚举, 直到 l
    int ans = 0;

    while (r >= l) {
        // 注意 c[r] 负责的区间长度是 lowbit(r)
        // 当区间左端点 r-lowbit(r)+r > l , 即没有抵达左边界 l 的时候，可以跳着走
        for (; r - lowbit(r) + 1 > l; r -= lowbit(r))
            ans = std::max(c[r], ans);
        // 当 r 和 l 之间没有 r 的子节点的时候，退化成枚举
        // 枚举一次，然后继续尝试跳
        ans = std::max(a[r--], ans);
    }

    return ans;
}

内层时间复杂度 logn，跳跃断点最多有 logn 个，也就是外层时间复杂度是 logn，所以总体时间复杂度 (logn)^2。

注意的是，此查询函数直接依赖着原数组 a[x]，所以，要确保原数组是及时更新的：

树状数组维护区间最值 - 单点修改 - C++ 实现

void update(int x, int v) {
    a[x] = v;  // 并更新原数组
    for (; x <= n; x += lowbit(x)) c[x] = max(c[x], v);
}

维护值域区间 ¶

树状数组的一个常见应用方式，是将原数组的值域作为区间。

这一点在后面的问题中都可以看到，在 DP 转移优化中也有应用 (比如 LIS 问题的 DP 优化)。

不过，树状数组说到底是在维护一个数组的前缀和或最值信息，所以理清楚这个原数组的定义是关键，有的时候这个「原数组」甚至不必要出现在代码中。

区间维护、单点查询 ¶

已知一个数列 a，你需要进行下面两种操作：
将某区间每一个数加上 d；
求出某一个数的值。
-- 来自洛谷 P3368、《算法竞赛进阶指南》 · 李煜东

当然，解决这个问题的前提是，要把两种操作都做到时间复杂度为 logn。

这是一个「区间维护」、「单点查询」问题，而树状数组擅长的是「单点增加」、「区间查询」，所以需要转化问题。

转化的关键是，把累积的区间增加操作，转化为另一个数组的前缀和。

新定义一个数组 b，元素全部初始化为 0。每次操作区间 [l,r] 上的每个 a[x] += d 的时候：

让 b[l] 单点增加 d
让 b[r+1] 单点减少 d

如此一来，b 数组的区间和即反映了原数组 a 的变化：

b[1, l-1] 区间上的前缀和没有发生变化。
b[l, r] 区间上的前缀和全部增加了 d，对应着 a 数组在此区间上的每一项元素增加了 d。
b[r+1, n] 区间上的前缀和没有发生变化，因为在 b[r+1] 处消除了影响。

也就是说， b 的前缀和 sum(b[1, x]) 映射到原数组的元素 a[x]，二者同步变化。

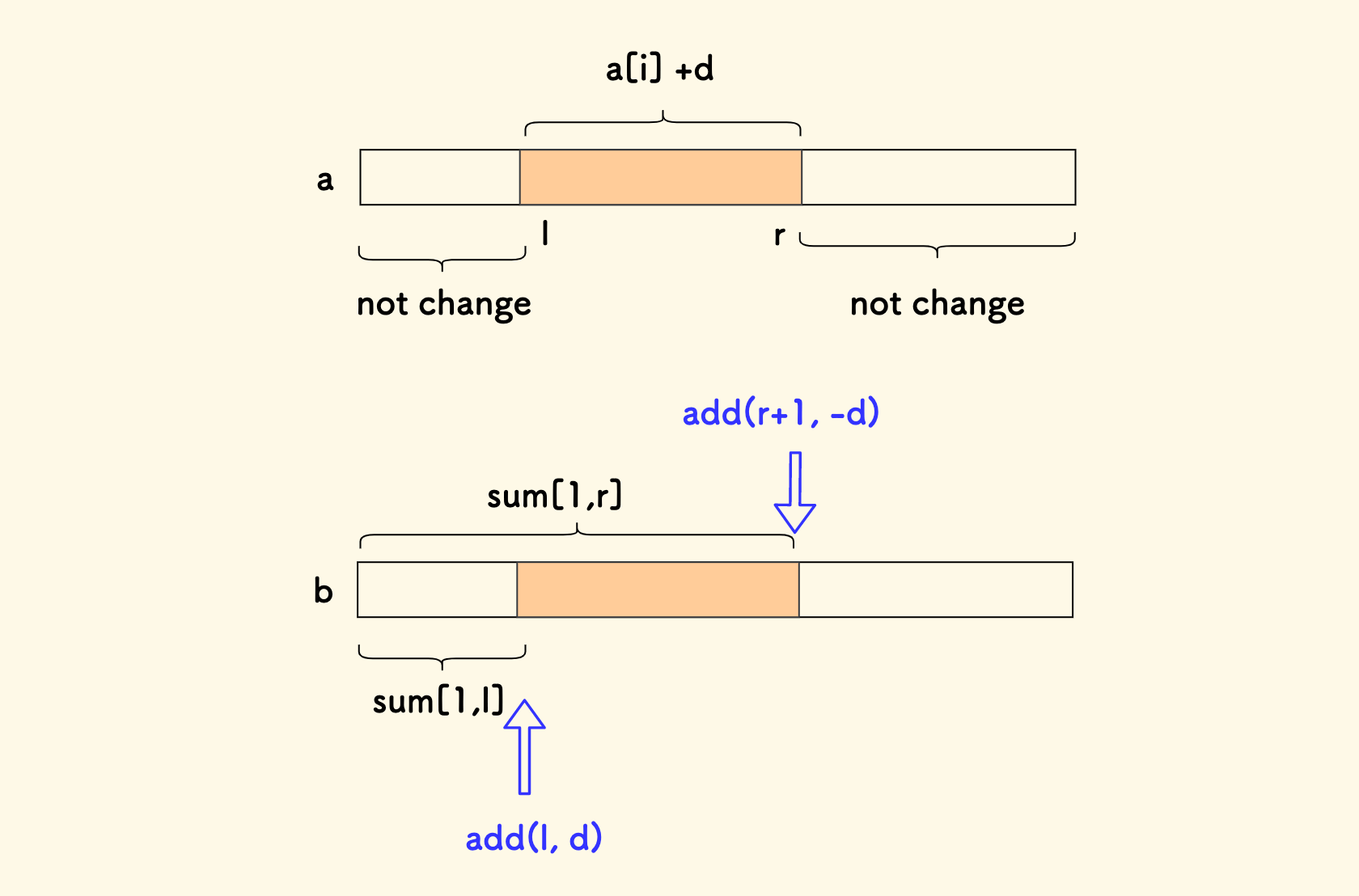
然后，建立一个树状数组维护 b 的前缀和即可，单点查询 a[x] 即查询 b 的前缀和 sum(b[1, x])，再加上 a[i] 的初始值。

可以知道，两种操作的时间复杂度都是 logn。

洛谷 P3368 - 区间增加、单点查询 - C++ 代码

逆序对问题 ¶

逆序对计数问题，是一个经典问题，一般来说，解法有两种：树状数组的解法和归并排序的解法。

对于给定的一段正整数序列 a，逆序对就是序列中满足 a[i] > a[j] 且 i < j 的数对，求数列中所有的这种数对的数量。
-- 来自洛谷 P1908

leetcode 上也有一道类似的题目：315. 计算右侧小于当前元素的个数。

假设数组 b[x] 维护值为 x 的元素数量，注意这是在原数组值域上的计数。

考虑从右向左扫描原数组 a，假设当前元素是 a[i] = x：

要维护计数数组 b[x]++
b 数组在区间 [1,x-1] 上的前缀和，就是历史上右侧的、值小于 x 的元素个数的计数。

比如说，下面图中，历史上已经扫描过的 a[k] 和 a[j]，它们在 b 数组中的计数是 b[5]=2。当扫描到 i 处时，由于此时的值更大，所以区间 [1,x-1] 内的所有计数的和，就是（以 x 为大的那个元素的）逆序对的数量。

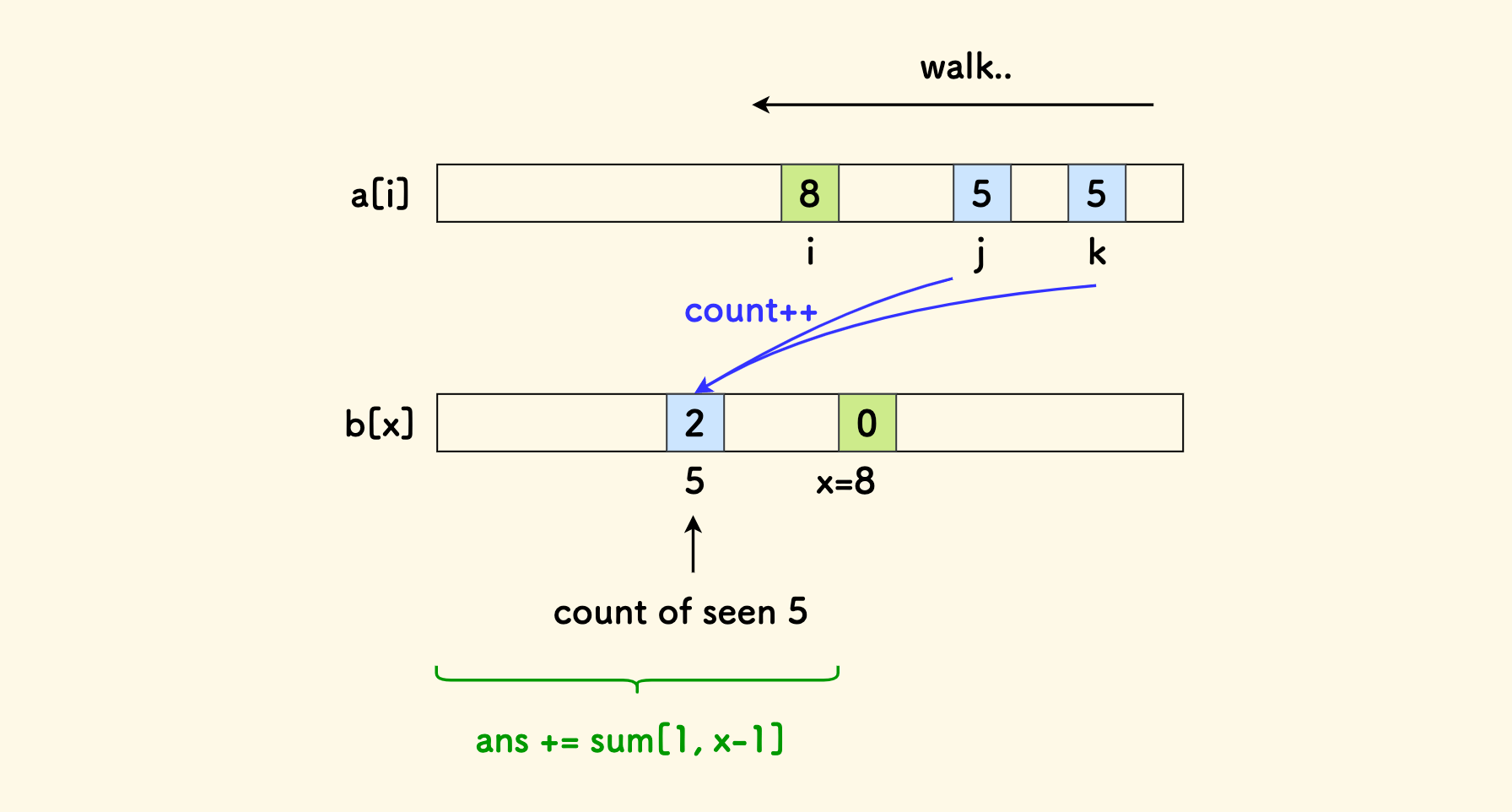
对 b 数组的维护，有「单点增加」和「求前缀和」，是典型的树状数组的用武之地。

伪代码大概如下：

int ans = 0;
int c[n+1]; // 树状数组
for (int i = n; i >= 1; i--) {
    int x = a[i];
    add(x, 1);
    ans += ask(x - 1);
}

再次可以看到，b 数组根本不会出现在最终实现的代码中，但是它却是理清整个过程的关键。

在实际操作中，由于原数组的值可能出现过大、负数等情况，有时还需要进行离散化处理，以方便使用树状数组。就是将值域范围映射到比较小的 [1,N] 范围上，而且这种处理同时不影响问题求解（比如只关心元素的大小关系、而不关心具体值的时候）。不过，离散化本身就需要用到排序，此时或许不如直接走归并排序求逆序对的解法。

洛谷 P1908 - 逆序对问题 - 树状数组解法 C++ 实现 - github

重建身高问题 ¶

这个题是真的有趣：

有 $n$ 头奶牛，已知它们的身高为 $1∼n$，且各不相同，但不知道每头奶牛的具体身高。现在这 $n$ 头奶牛站成一列，已知第 $i$ 头牛前面有 $A_{i}$ 头牛比它低，求每头奶牛的身高。
-- 来自 AcWing 244. 谜一样的牛、《算法竞赛进阶指南》 · 李煜东

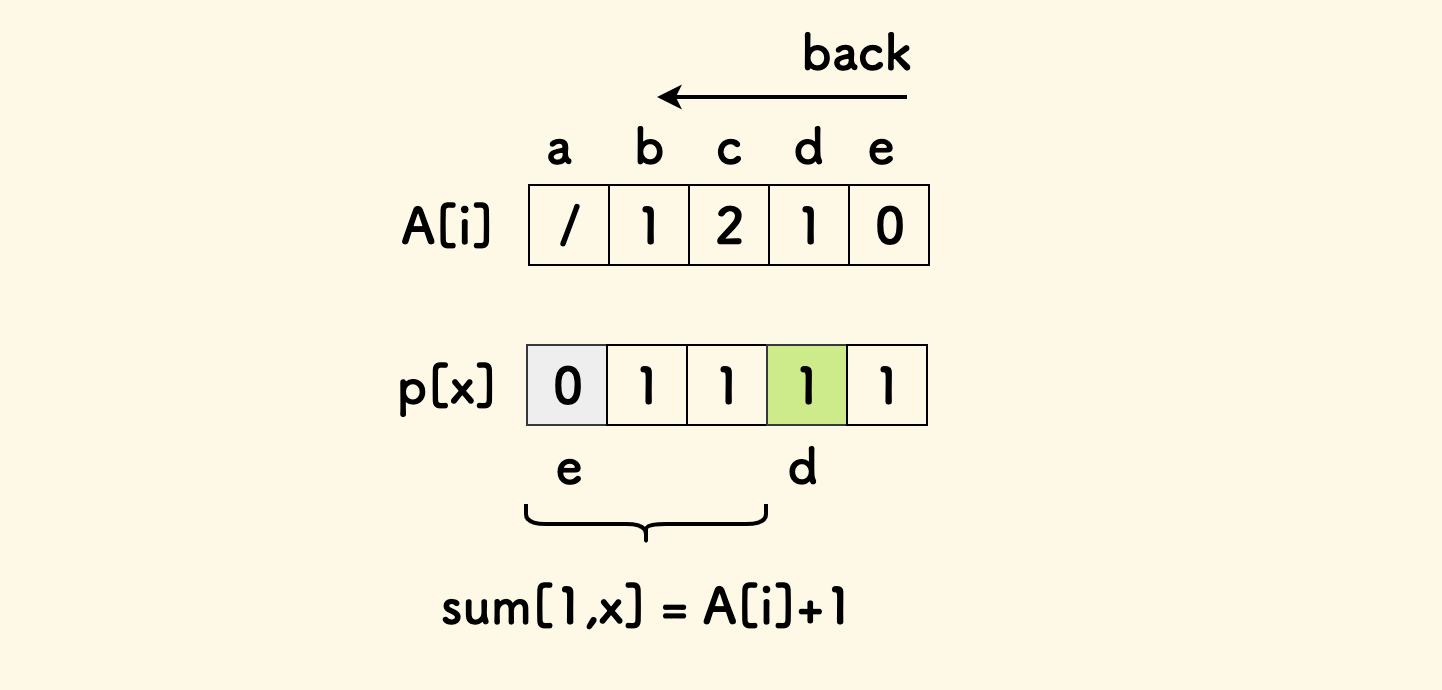
比如说，输入的 n=5，A 数组是 1,2,1,0，注意第 1 头牛前面没有牛，所以并没有将它列出。此时的奶牛身高应该是 2,4,5,3,1。

对于最后一头奶牛，毫无疑问，如果它前面有 k 个奶牛比它低，那么它应该在整个队列中的身高是第 k+1 小。在这个例子中，假设 5 头奶牛分别叫做 a,b,c,d,e。那么最后一头奶牛 e 的身高应该等于 1。

接下来考虑倒数第二头奶牛 d，因为它前面有 1 头比它低，那么应该排除它身后的奶牛 e 之后，处于第 2 大。下图中，height 是按身高从低到高排列的，奶牛 d 会落在 3 号位置，也就是身高是 3：

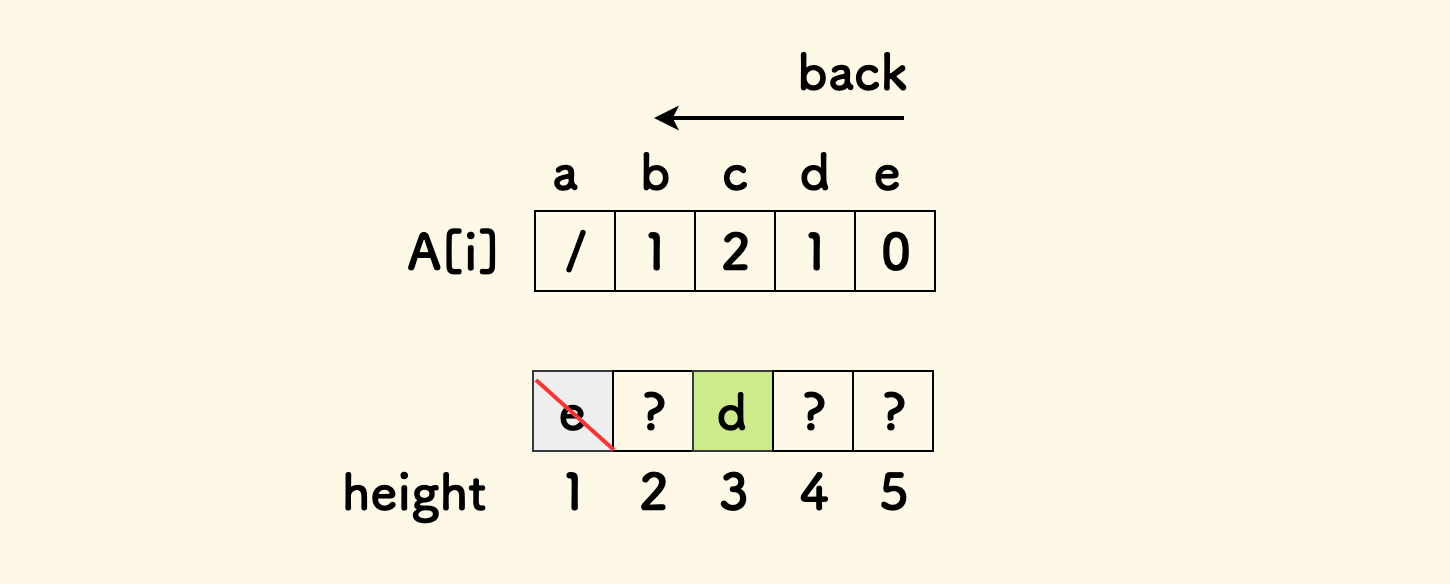
如此规律的话，可以考虑从后向前扫描：每次安置一头奶牛 i 时，跳过已经安置好的奶牛，从前向后数，落在第 A[i]+1 个位置。

下图演示了整个安置过程：

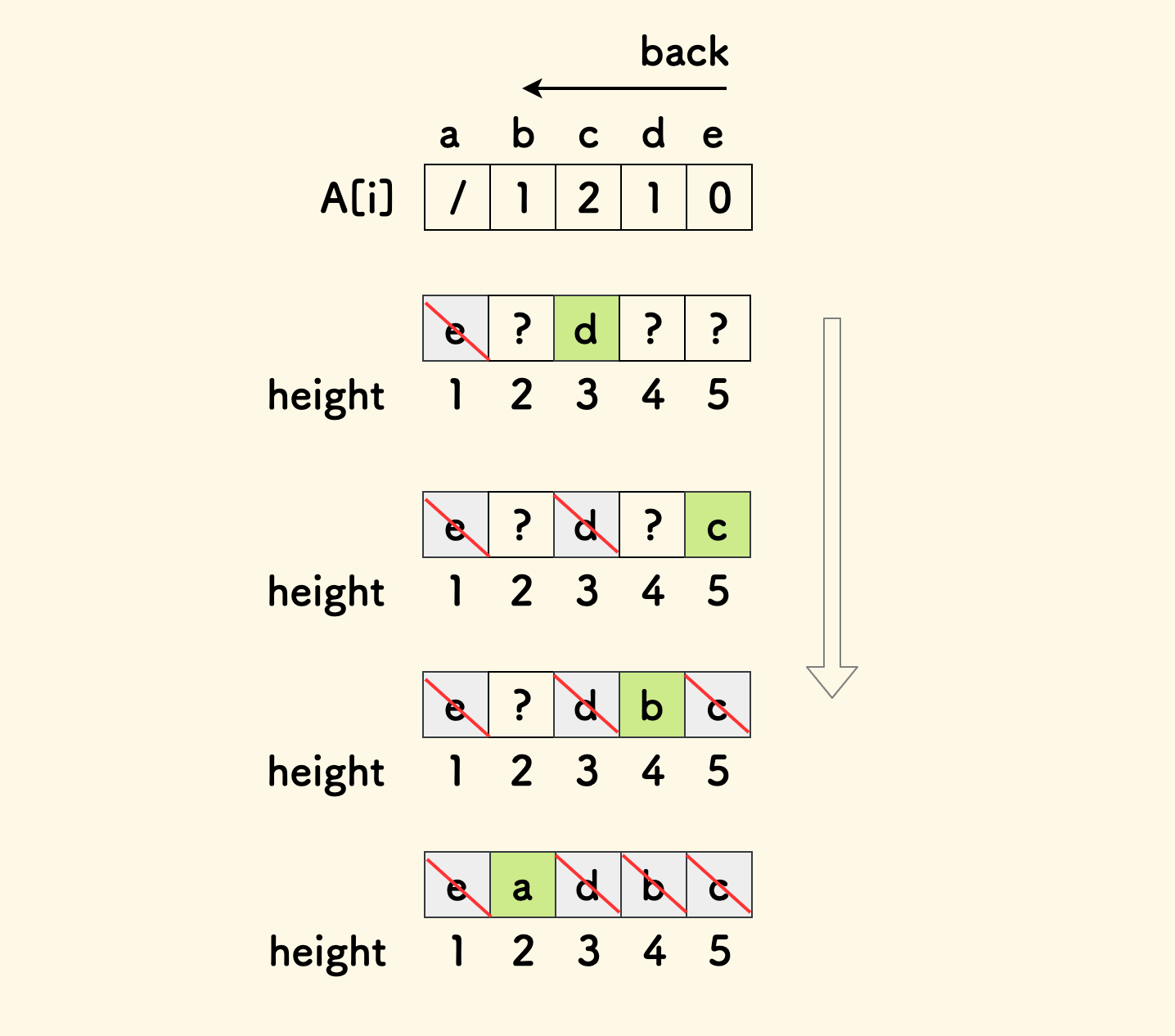
可以知道所有奶牛的身高：a=2, b=4, c=5, d=3, e=1。

但是，结果是分析出来了，代码该怎么设计呢？

第 i 头奶牛前面有 A[i] 头奶牛比它低，这实际是对前面所有比它低的奶牛的一种计数，可以考虑前缀和对标志位数组计数。

定义数组 p[x]，全部初始为 1。其含义是身高为 x 的奶牛是否已经安置，如果已经安置，则置 0。考虑第 i 头奶牛时，假设 A[i]=k 的话，要跳过身后已经安置的奶牛，找到第 k+1 个位置，因为已经安置的位置会被置 0，所以实际上是找 p 数组的前缀和至少为 k+1 的左界。

维护 p 数组需要支持：

单点修改：置零。
前缀求和。

所以可以用一个树状数组来维护，然后每次安置一头奶牛的时候，二分答案找满足 ask(x) >= k+1 的左界即可。

大概的伪代码如下，时间复杂度是 $n(\log{n})^2$。

int c[n+1]; // c 维护 p 数组的前缀和
for (int i = 1; i <= n; i++) add(i, 1);

for (int i = n; i >= 1; i--) {
    // 二分答案
    int l = 1, r = n;
    while (l < r) {
        int m = (l + r) >> 1;
        if (ask(m) >= a[i] + 1) r = m;
        else l = m + 1;
    }
    ans[i] = l;  // l 就是要放入的位置，也就是身高
    add(l, -1); // 置零
}

这个问题可以再次看到，定义数组 p 是使用树状数组的关键点，而它甚至都没有出现在最终的代码里。

AcWing 谜一样的牛 - C++ 实现 - github

三元上升子序列 ¶

在含有 $n$ 个整数的序列 $a_{1}$，$a_{2}$，…$a_{n}$ 中，三个数会被称作一个三元上升子序列，当且仅当 $i < j < k$ 且 $a_{i} < a_{j} < a_{k}$ 。求一个给定数列中的三元上升子序列的总个数。
-- 洛谷 P1637

比如数组 [1,2,2,3,4] 中三元上升子序列的个数是 7，分别是：

[1, 2, 2, 3, 4]
[1, 2, 2, 3, 4]
[1, 2, 2, 3, 4]
[1, 2, 2, 3, 4]
[1, 2, 2, 3, 4]
[1, 2, 2, 3, 4]
[1, 2, 2, 3, 4]

考虑三元序列的中间的数 a[j]，固定好它之后，它能形成的三元上升序列的个数，应该是左边比它小的元素个数乘上右边比它大的元素的个数。

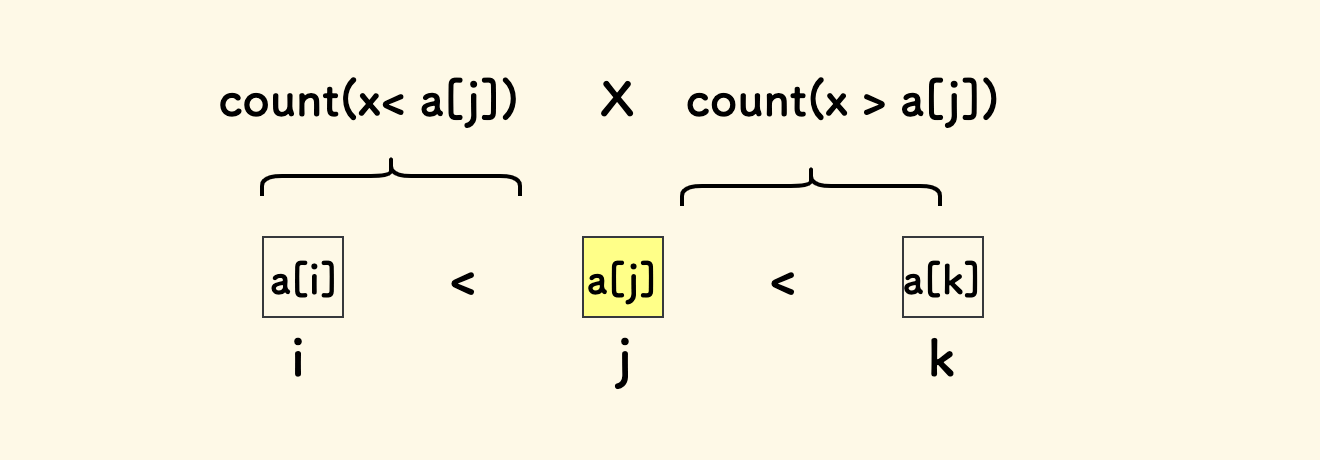
于是拆分成两个子问题：

求每个元素左边有多少个比它小的。
求每个元素右边有多少个比它大的。

从求逆序对的问题可以知道，这种问题，可以用树状数组来解决。

求每个元素左边右多少比它小的，可以从左到右扫描原数组。
定义一个数组 b[x] 维护值为 x 的数量，用一个树状数组来维护它。
遇到一个值为 x 的元素，则进行计数 add(x, 1)。
由于是自左向右扫描，左边的元素会先计数。
那么当前元素 x 的左边比它小的计数就是前缀和 sum[1,x-1]，也就是 ask(x-1)
伪代码大概是：
```
int ap[n+1]; // 维护 a[i] 左边有多少比它小的元素
for (int i = 1; i <= n; i++) {
    ap[i] = ask(a[i]-1);
    add(a[i], 1);
}
```
求每个元素右边多少比它大的，可以从右向左扫描原数组。
分析和上面类似，不同点只是求解的是值域 [x+1, N] 上的计数和，不再展开讨论。
伪代码大概是：
```
int aq[n+1]; // 维护 a[i] 右边有多少比它大的元素
for (int i = n; i >= 1; i--) {
    aq[i] = query(a[i]+1, N); // N 是 a[i] 的最大值
    add(a[i], 1);
}
```

最后，三元上升序列的数量，就是对每个可能的 a[j]，计算二者乘积，再累加就行：

for (int j = 2; j <= n-1; j++) ans += aq[j] * aq[j];

洛谷 P1637 - C++ 实现 - github

模板代码 ¶

结尾语 ¶

树状数组的代码简洁优美，最后一些总结：

擅长单点增加、区间查询。
也可以维护区间最值。
分析的关键是，理清原数组的含义。
树状数组也经常用在值域上，必要时可以提前离散化。
典型应用：逆序对问题、1D DP 转移优化等。
计数有时候也可以看成一种求和。

Update 2024/04/30：

树状数组非常「清凉」、小巧精炼，相对于原数组来说、只需要一倍空间。

其实也有一个关键缺点，所支持的运算必须要可以由单点来直接应用到区间，比如求和操作、最值操作等等，单点更新可以直接求解其影响的祖先区间的修改。但是某些操作则不尽然，比如逻辑操作符，或运算、与运算是需要两个拆半的区间来综合推导的，就不再适合树状数组，这种情况下线段树却很适合，但是需要至少 4 倍空间。

（完）

本文参考：《算法竞赛进阶指南》· 李煜东

树状数组的原理、结构 和 典型应用