最近又重新做了下经典的最长上升子序列 LIS 的两个问题,尝试了三种新的方法。
本文记录「经典 LIS 问题」和「有限上升 LIS 问题」的基于动态规划转移优化的三种解法,分别基于树状数组、CDQ 分治 和 平衡树。
关于经典 LIS 问题,本博客已经有三篇文章讲了三种方法
- 朴素的
O(n2)DP 解法 - 二分 + 贪心的解法、以及 DAG 模型推广
- (本文)基于朴素 DP 解法 - 进一步优化 DP 转移
经典 lis 问题 ¶
经典的 LIS 问题,描述如下:
在一个数组中找到最长的、元素严格递增的子序列。 并不要求这个序列在原数组中连续,但是其中元素的相对顺序要和在原数组中保持一致。
-- leetcode 300 最长递增子序列
朴素的 DP 思路 (其分析可以参考 LIS DP 解法),伪代码如下。 可以看到目前的动态规划转移时间是 $O(n)$,接下来的思路都是在优化这个 DP 转移。
int dp[n]; dp[0] = 1;
for (int i = 1; i < n; i++) {
for (int j = 0; j < i; j++)
if (a[j] < a[i]) dp[i] = max(dp[i], dp[j]+1);
ans = max(ans, dp[i]);
}
树状数组优化转移
前置知识点:树状数组原理,熟悉的话,可以略过。
对原来的 DP 思路稍做改变,定义原数组 a 的值域上的 dp[x], 其含义是,以值 x 结尾的能形成的最长上升子序列的长度。
自左向右扫描,可以归纳出递推逻辑:
dp[x] = max(dp[x], dp[v] + 1),其中 v 是已经扫描过的所有严格 < x 的 a[j] 的值。
下面的图可以帮助理解这个递推关系,细节则不再展开讨论。
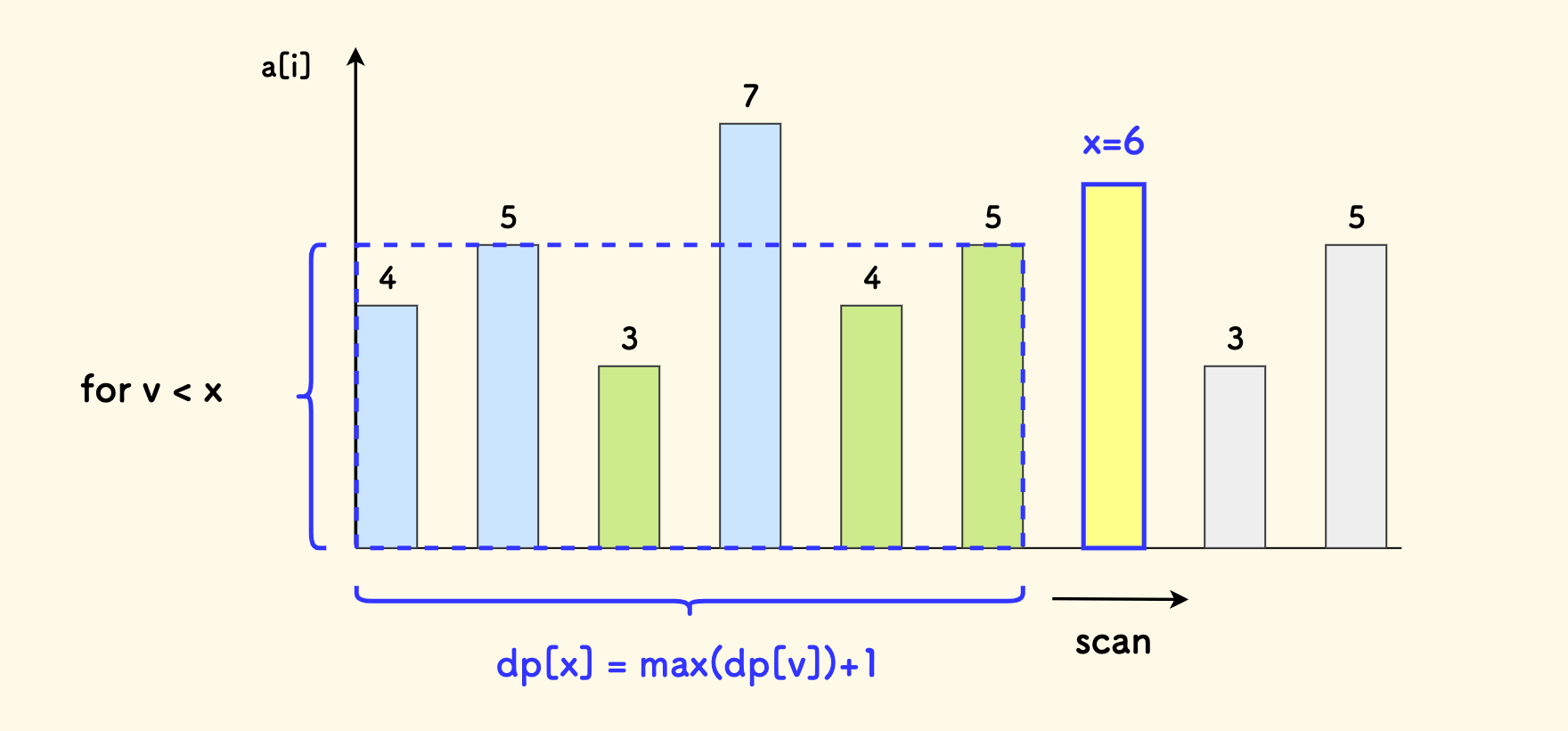
递推关系也可以写成:
// v 是已经扫描过的 且 < x 的 a[j] 的值
dp[x] = max(dp[v], for each v < x) + 1;
采用树状数组来维护此 dp 数组的区间最值即可:
- 查询区间
[1,x-1]上维护的dp最大值 - 加一后得到
dp[x],进行单点维护
大概的伪代码如下,其中:
update为树状数组单点更新函数ask为树状数组前缀区间最值查询函数
int mx = max(a); // 最大值
int dp[mx];
for (auto x : a) update(x, ask(x-1) + 1);
ans = ask(mx); // 答案
具体的实现代码见下方链接,其中考虑到输入的原数组的值域过大、有负数等情况,进行了离散化预处理(相关离散化的文章)。
时间复杂度是 $O(n\log({max(a)}))$,如果进行离散化处理的话,也可以说是 $O(n\log{n})$ 的。
经典 LIS 问题 - 树状数组 - 值域 DP 优化 C++ 实现 - github。
平衡树解法
和树状数组的思想一样,平衡树的解法也是一种数据结构优化 dp 转移的手段,这里采用 fhq treap [1]。
仍然是在优化下面的转移关系:
// v 是已经扫描过的 且 < x 的 a[j] 的值
dp[x] = max(dp[v], for each v < x) + 1;
fhq treap 的 split 操作可以根据一个给定的数值 v,把树分成两个子树, 使得左子树中所有节点的权值全部不大于 v,右子树中所有节点的权值全部大于 v。
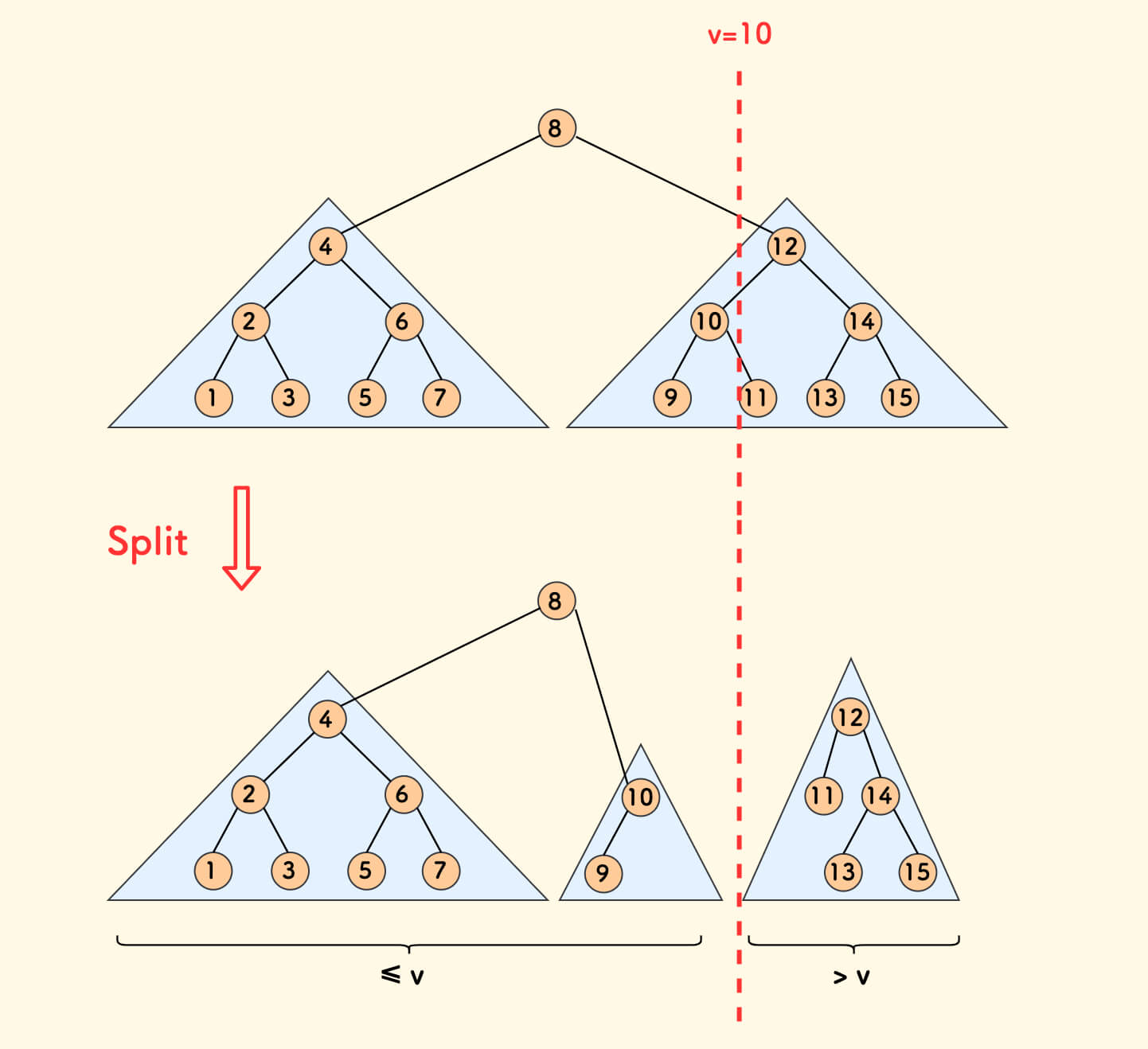
在每个节点上额外维护两个信息:
- 以当前节点的权值
val结尾的 LIS 长度len,也就是上面说的dp[val] - 当前节点代表的子树中最大的 LIS 长度
mxlen,也就是子树中最大的 dp 值。
fhq treap 中的节点 C++ 定义
struct {
int l, r; // 左右孩子节点
int val; // BST 的权值, 即 nums 数组中的元素值 x
int rnd; // 堆的随机值
int size; // 树的大小
int len; // 以 val 结尾的 lis 的长度, 也就是 dp[val]
int mxlen; // 当前子树中的最大的 lis 长度,也就是子树内最大的 dp[val]
} tr[N];
首先,要解决的问题是,如何维护这两个信息。
fhq treap 的核心操作「分裂」和「合并」都是一种不断递归的过程,有一个 pushup 函数穿插其中,原本是用来维护各个子树的大小的。
pushup 是在递归过程中的后序函数,自底向上地通过左右子树维护父树的信息。
fhq treap 中的 分裂、合并 和 pushup 函数 C++
void pushup(int p) {
tr[p].size = tr[tr[p].l].size + tr[tr[p].r].size + 1;
}
// 按给定的 v 值来分裂成两个子树 x 和 y
// 分裂后 x 的所有权值都 <= v,y 的所有权值都 > v
void split(int p, int v, int &x, int &y) {
if (!p) {
x = y = 0;
return;
}
if (tr[p].val <= v) {
x = p;
split(tr[p].r, v, tr[p].r, y);
} else {
y = p;
split(tr[p].l, v, x, tr[p].l);
}
// pushup 是自底向上的穿插
pushup(p);
}
// 合并两个子树 x 和 y
// 注意要求:x 中的所有权值要不大于 y 中的
int merge(int x, int y) {
if (!x || !y) return x + y;
if (tr[x].rnd < tr[y].rnd) {
tr[x].r = merge(tr[x].r, y);
pushup(x);
return x;
} else {
tr[y].l = merge(x, tr[y].l);
pushup(y);
return y;
}
}
我们可以借路 pushup 函数来维护 mxlen 字段, 维护过程如下图所示,其中节点上的数字表示 maxlen:
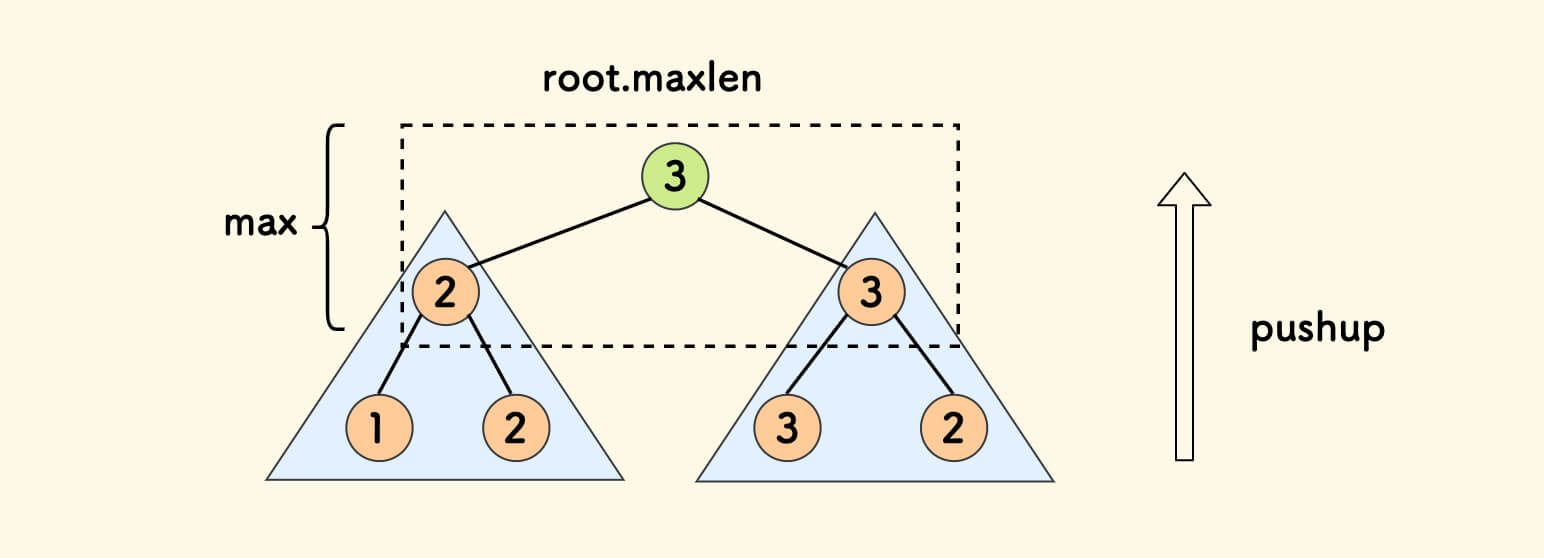
pushup 维护 maxlen 字段 - C++ 代码
void pushup(int p) {
tr[p].size = tr[tr[p].l].size + tr[tr[p].r].size + 1;
tr[p].mxlen = tr[p].len; // 至少为当前节点的 lis len
// 再和左右子树比较,取最值
if (tr[p].l) tr[p].mxlen = max(tr[p].mxlen, tr[tr[p].l].mxlen);
if (tr[p].r) tr[p].mxlen = max(tr[p].mxlen, tr[tr[p].r].mxlen);
}
下面考虑主过程,可以扫描原数组 nums 的每一项元素值 x:
按
x-1执行分裂后,左子树中所有的权值都严格小于x。构造一个询问函数
ask(v),它返回权值不大于v的子树上最大的 LIS 长度mxlen:ask 函数的 C++ 实现
int ask(int v) { // 先分裂为左子树 x 和右子树 y int x, y; split(root, v, x, y); // 此时 x 的所有权值 val 都不大于 v int ans = tr[x].mxlen; // 搞完以后,要记得把两个子树再合并回去 root = merge(x, y); return ans; }取左子树的
mxlen,再加一,就是以x结尾能形成的最长的 LIS 的长度len。 新建一个节点,插入到 treap 中。插入新节点的实现代码如下:
insert 函数的 C++ 实现
int newnode(int v, int len) { tr[++n].val = v; tr[n].rnd = rand(); tr[n].size = 1; tr[n].len = len; tr[n].mxlen = len; return n; } void insert(int v, int len) { int x, y; split(root, v, x, y); int z = newnode(v, len); root = merge(merge(x, z), y); }最终的答案就是根节点的
mxlen。
所以,最终的求解主流程代码如下,时间复杂度是 $O(n\log{n})$。
FHQ treap;
for (auto x : nums) {
int mxlen = treap.ask(x - 1);
treap.insert(x, mxlen + 1);
}
return treap.tr[treap.root].mxlen; // 根上的 mxlen 就是答案
最终的完整实现代码: 经典 LIS 问题 - 平衡树 - 值域 DP 优化 C++ 实现 - github。
可以看到,treap 的解法比树状数组的要稍微复杂一点,不过免去了离散化的烦恼。
CDQ 分治优化转移
CDQ 分治的是一种分治思想:
- 二分要处理的区间,分成左右两边。
- 先递归处理左边。
- 然后计算左边对右边的贡献。
- 再递归处理右边。
用伪代码来描述这个过程:
void cdq(int a[], int start, int end) {
int mid = (start + end) >> 1;
// 递归处理左边
cdq(a, start, mid);
// TODO: 计算左边对右边的贡献
// 再递归处理右边
cdq(a, mid+1, end);
}
CDQ 分治和归并排序很像,归并求逆序对数量 可以看做一种 CDQ 分治。
现在将考虑如何用 CDQ 分治的思路解决 LIS 问题。
仍然采用经典的 LIS 的 dp 定义方式,即 dp[i] 的含义是以位置 i 结尾的能形成的最长上升子序列的长度。 容易知道,递推关系是:
// j 为 < i 的且满足 a[j] < a[i] 的下标
dp[i] = max(dp[j], for each a[j] < a[i]) + 1;
关键在于考虑,CDQ 分治过程中,如何计算左边对右边的贡献。
二分当前区间后,把左右两边分别排序。
此时左边已经递归处理完毕了,也就是左边的任一个 dp[j] 的含义已经是,左边区间内能形成的以 a[j] 结尾的 LIS 的长度。
考虑左边对右边每一个 i 的影响:
- 找到左边所有小于
a[i]的元素的下标j。 - 取其中
dp值最大的那个,dp[i]至少为max(dp[j]) + 1。
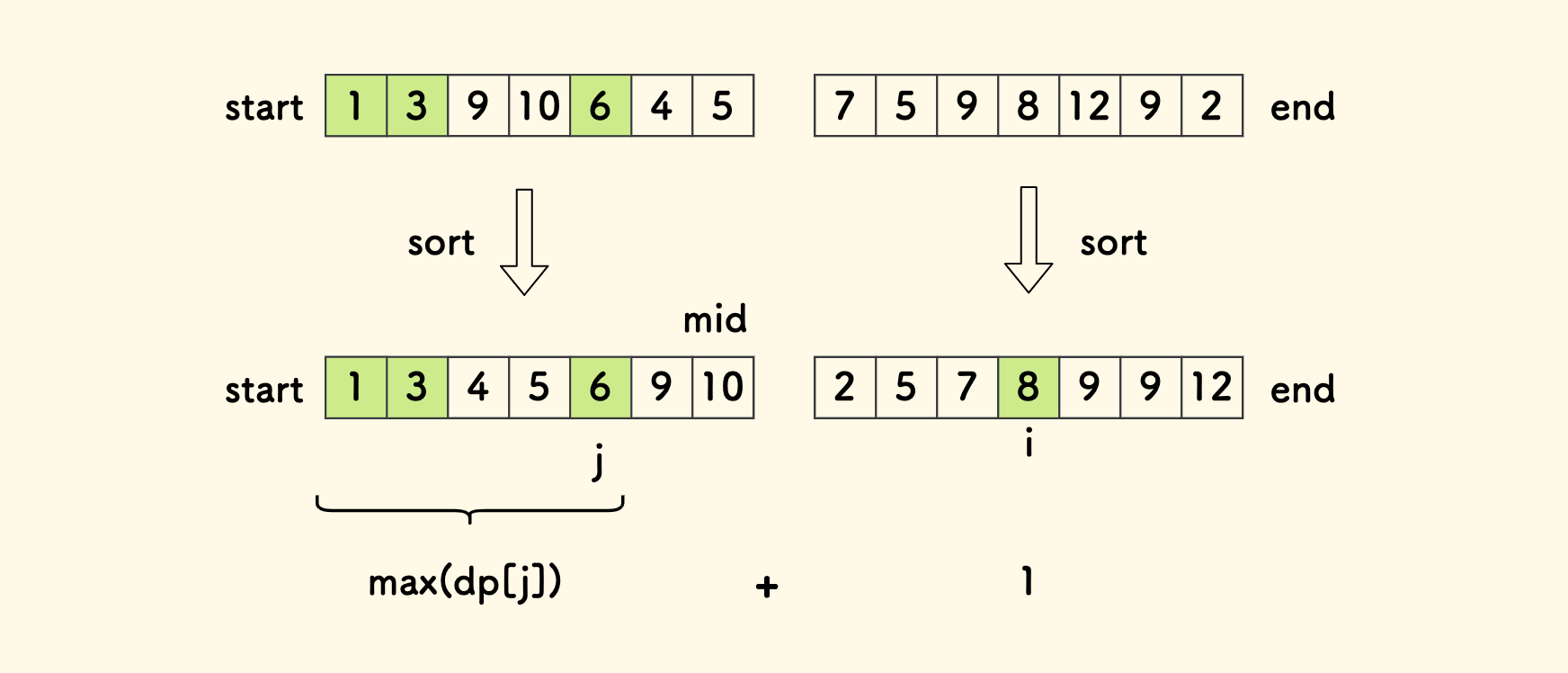
大概伪代码是:
for (int i = mid+1; i <= end; i++) {
int ma = 0;
for (int j = start; j <= mid; j++)
if (a[j] < a[i]) ma = max(ma, dp[j]);
dp[i] = max(dp[i], ma) + 1;
}
但是这段代码的时间复杂度是平方级别的,其实可以优化。
因为左右两段都已经排序好了,所以 没有必要回溯 j。
原因在于,下一次计算 i+1 的时候,当前的 j 和其左边都一定小于 a[i+1],因为 i 右移了,值增大了, 所以只需要进一步右移 j 即可,直到不满足 a[j] < a[i] 停止。
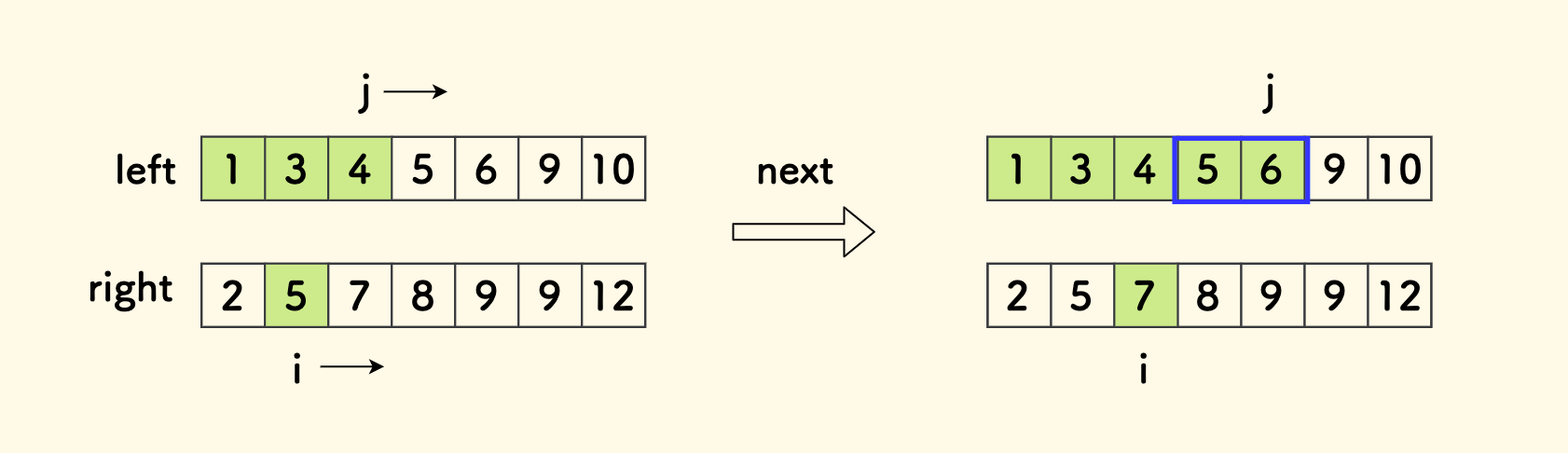
代码进一步优化成下面的样子,虽然是两层循环,但是内层并无回溯,所以总体时间复杂度是线性的。
int ma = 0, j = start, i = mid+1;
while (i <= end) {
while (j <= mid && a[j] < a[i]) ma = max(ma, dp[j++]);
dp[i] = max(dp[i], ma) + 1;
i++;
}
由于还没有处理右半段区间,dp[i] 的值只可以说是「至少是」这些,还无法盖棺定论。
再处理右边之前,要提前恢复右边的顺序,因为 LIS 问题是按原顺序而言的, 我们事先排序只是为了计算左边对右边的贡献。恢复顺序可以考虑按下标重新排序。
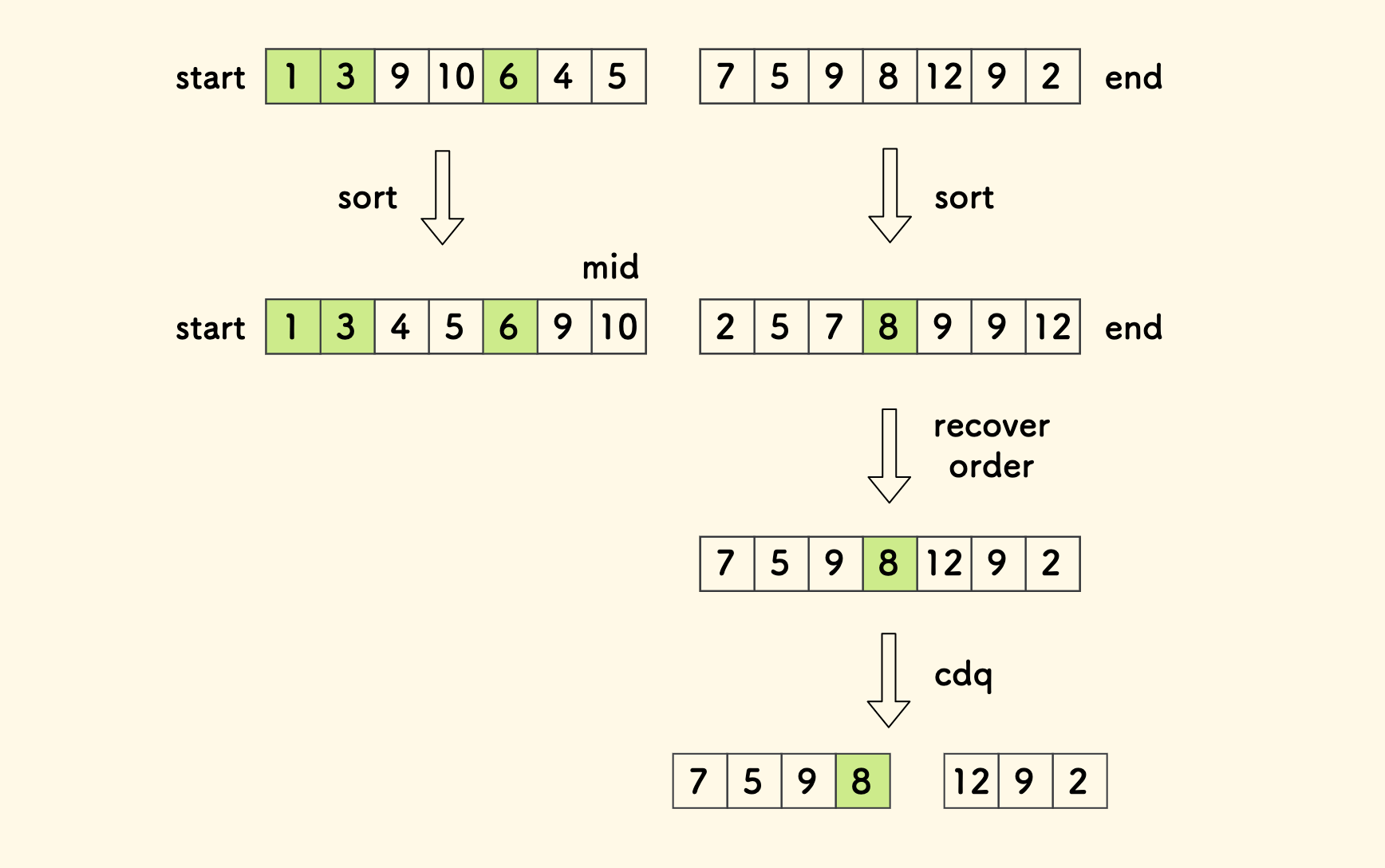
整个过程和归并排序相似,整体的伪代码如下:
void cdq(int a[], int start, int end) {
int mid = (start + end) >> 1;
// 递归处理左边
cdq(a, start, mid);
// 左边右边分别排序, 按值排序
sort(a, start, mid), sort(a, mid+1, end);
// 计算左边对右边的贡献
int ma = 0, j = start, i = mid+1;
while (i <= end) {
while (j <= mid && a[j] < a[i]) ma = max(ma, dp[j++]);
dp[i] = max(dp[i], ma) + 1;
i++;
}
// 恢复右边的顺序, 按下标排序
sort(a, mid+1, end, cmp_i);
// 再递归处理右边
cdq(a, mid+1, end);
}
最终 dp 数组中的最大值就是答案。
复杂度分析上,类似归并排序,递归深度 $\log{n}$,每次处理中存在 $n\log{n}$ 排序,所以整体时间复杂度是 $O(n(\log{n})^2)$。
经典 LIS 问题 - CDQ 分治 - C++ 实现 - github。
不过,CDQ 分治远没有 LIS 的其他解法简洁,时间复杂度也不是最优,这里权当一种新的解法来给出。
有限上升 LIS 问题 ¶
有限上升的意思是说,在经典的 LIS 问题基础上,限制序列的相邻元素之差不超过一个给定的数字 k。 问题来自 leetcode 2407. 最长递增子序列 II:
给你一个整数数组 a 和一个整数 k 。找到 a 中满足以下要求的最长子序列:
- 子序列 严格递增
- 子序列中相邻元素的差值 不超过 k 。
请你返回满足上述要求的 最长子序列 的长度。 子序列 是从一个数组中删除部分元素后,剩余元素不改变顺序得到的数组。
基于前面的讨论,这个问题也可以有「DP + 树状数组优化」和「DP + CDQ分治」两种思路。
DP + 树状数组优化
基于 前面经典 LIS 的树状数组解法的讨论, 有限上升 LIS 问题无非是限制了 DP 转移时的来源值域范围要在一个区间内。
现在的 DP 转移逻辑变成了:
// v 是已经扫描过的 且满足 x-k <= v < x 的 a[j] 的值
dp[x] = max(dp[v], for each x-k <= v < x) + 1;
也就是说,要求 DP 转移来源的值要在区间 [x-k, x-1] 内。
树状数组也可以维护「单点修改、查询区间最值」的,详情可以参考 这篇文章。
当然,线段树也是可以的。
伪代码如下,其中 query 是查询区间最值的函数。
需要注意的细节是,要防止 x-k 是负数的情况:
int mx = max(a); // 最大值
int dp[mx];
for (auto x : a) update(x, query(max(x-k, 1), x-1) + 1);
ans = ask(mx); // 答案
树状数组查询区间最值的时间复杂度是 $(\log{n})^2$, 所以此解法的时间复杂度是 $O(n(\log{n})^2)$。
有限上升 LIS 问题 - 树状数组 - 值域 DP 优化 C++ 实现 - github。
DP + CDQ 分治
基于 前面讨论的经典 LIS 问题的 CDQ 分治方法,需要变化的地方在于「计算左边对右边的贡献」这一部分。
原本只需要对右边的每一个 i,计算左边满足 a[j] < a[i] 的所有 j 的 max(dp[j]) 即可, 现在要加一个限定,就是要同时满足 a[i] - a[j] <= k。
对于每一个右边的 i,左边参与决策的 j 不能再只维护一个变量了, 而是需要在一个符合条件的窗口内的多个 j 来决策这个最大值。
这是经典的「滑动窗口求最值问题」,经典的解法是采用单调队列,均摊时间 $O(n)$ 。
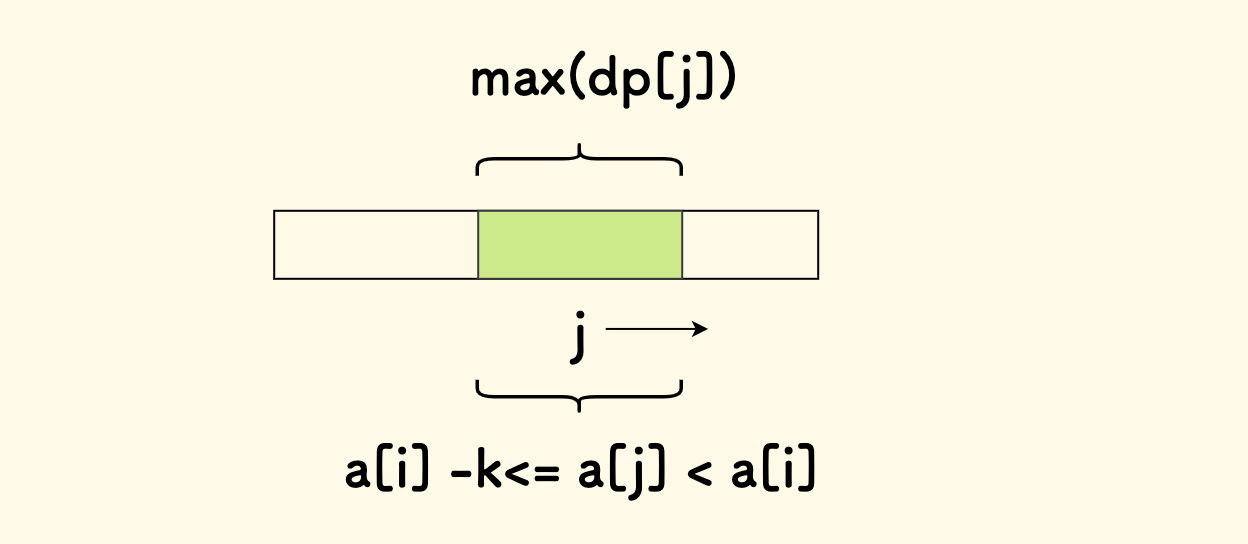
要维护窗口内最大值,因此采用单调递减队列,也就是 要求队头到队尾始终满足 DP 值严格递减性质。
- 队尾维护:每加入一个
j到队尾时,都要提前从队尾弹出比j的 DP 值 更小的元素。 - 队头维护:因为已排序,队头的元素值更小,一旦不满足
k的约束,则弹出。 - 单调队列的队头是符合条件的最大值。
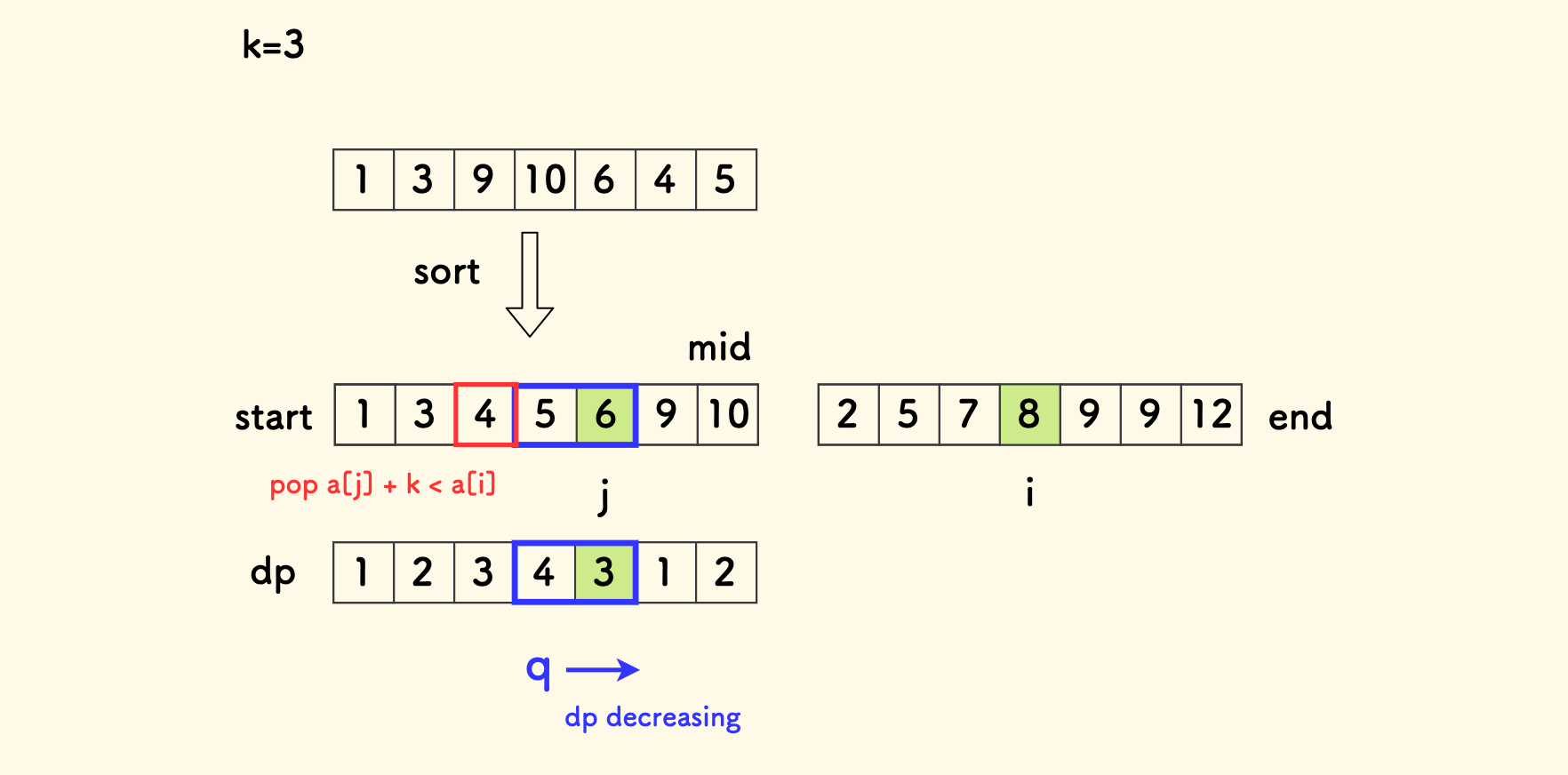
用伪代码来描述大概是:
deque q; // 填入下标
while (j <= mid && a[j] < a[i]) {
// 队尾维护:保证单调递减
while (!q.empty() && dp[q.back()] < dp[j])
q.pop_back();
// 加入新的 a[j]
q.push_back(j++);
// 队头维护:保证满足 a[i] - a[j] <= k
while (!q.empty() && a[q.front()] + k < a[i])
q.pop_front();
}
// 队头的 DP 值最大
dp[i] = max(dp[i], dp[q.front()] + 1);
回头看一下之前 经典 LIS 问题 CDQ 分治解法的代码。 由于我们只是改变了最值的获取方式,在两边都有序的情况下,每次迭代右边的 i 时,仍然无需回溯左边的 j, 而且队列 q 也无需清空。
总体的伪代码如下,虽然有三层循环,但是每个 j 只会入队一次、最多出队一次,而且 j 不会回溯,所以其时间复杂度仍然是线性的。
deque q; // 填入下标
int j = start, i = mid+1;
while (i <= end) {
while (j <= mid && a[j] < a[i]) {
// 队尾维护:保证单调递减
while (!q.empty() && a[q.back()] < a[j])
q.pop_back();
// 加入新的 a[j]
q.push_back(j++);
// 队头维护:保证满足 a[i] - a[j] <= k
while (!q.empty() && a[q.front()] + k < a[i])
q.pop_front();
}
// 注意再排除下队头不符合条件的情况
// 因为上面的子循环可能根本不会进入, 但是 a[i] 已经更换到一个新的
while (!q.empty() && a[q.front()] + k < a[i])
q.pop_front();
// 细节没有写出: q empty 的情况
dp[i] = max(dp[i], dp[q.front()] + 1);
i++;
}
总的代码框架和经典 LIS 问题的 CDQ 解法代码一致。 整体时间复杂度仍然是 $O(n(\log{n})^2)$
有限上升 LIS 问题 - CDQ 分治 C++ 实现 - github。
可以看到 CDQ 分治虽然可以做,但是已经变的很复杂了。在 leetcode 上 虽然可以 AC,但是跑的比树状数组和线段树的解法要慢许多。
(完)
更新记录:
- 2024/01/08 - 添加经典 LIS 问题的平衡树解法。
相关阅读:
