一致性哈希算法是一种特殊的哈希算法, 当目标槽位数量发生变化时,它会尽力降低的重新映射的数量。 传统的哈希表设计中,添加或者删除一个槽位,会造成全量的重新映射, 一致性哈希则追求的是增量式重新映射。 一致性哈希最早由Karger在1997年提出,多用于分布式系统中的扩容缩容问题、 分布式哈希表的设计等等。
本系列共分为四部分:
本文是第一部分, 将从一个kvdb的设计谈起,解答「为什么需要一致性哈希」的问题。
如何代理一个简单的kvdb? ¶
假如我们有一个简单的kvdb (key-value-database), 它支持两个简单的操作:
- $set(k, v)$ 表示把键为 $k$ 的值更新为 $v$。
- $get(k) \rightarrow v$ 表示查询键为 $k$ 的值为 $v$。
由于单节点系统的服务能力有限, 因此我们要考虑多节点的架构方案。 一种简单的架构方案是:前面做一个代理服务,把请求分割到不同的后端节点上, 这是常说的sharding模式。
下面的图1.1是这个kvdb的架构图, 蓝色的节点是一个代理服务器, 负责为到来的读写请求分配一个后端节点。 后面的紫色的节点都是存储节点。
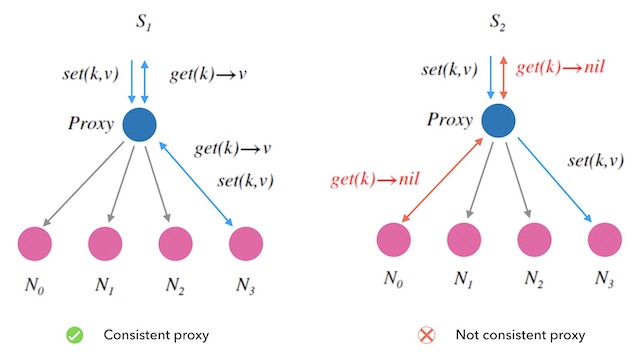
可以看到左边的 $S_1$ 总会给同一个 $k$ 分配不变的后端节点, 而右边的 $S_2$ 则不然, 它先给 $set(k,v)$ 分配了 $N_3$, 又为后续的 $get(k)$ 分配了 $N_0$ , 导致 $get$ 读取失败, 所以 $S_2$ 是无法正确地工作的。 我们称 $S_1$ 的代理方式是有一致性的, $S_2$ 的则没有。
我们将寻找一种有一致性的代理方案: 对同一个 $key$ 的所有读写请求都必须一致地分配给同一个后端节点。 同时,分配的负载应该尽量均衡。
换句话讲, 我们需要寻找一种映射函数, 把随机到来的字符串 $key$ ,一致地映射到 $n$ 个槽中。 此外,我们也希望,这个映射要做到尽量平均。
简单的哈希映射 - Mod-N哈希 ¶
哈希表是一种常用的基本数据结构。 例如下面图2.1,它把随机到来的字符串 $k$ 输入到哈希函数 $hash$ 中, 然后映射到一张连续内存表上。
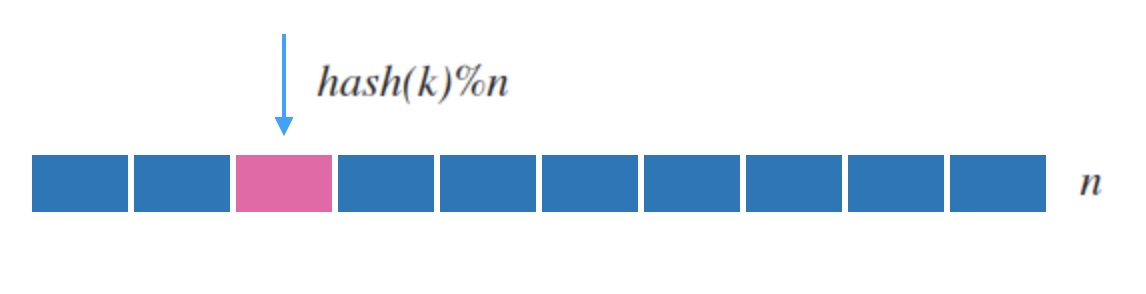
一般地,常见的哈希函数(如 md5, sha1)都是映射到uint32这样很大的空间的, 所以哈希表一般对哈希函数的结果取余数来映射到槽位, 即 $hash(k) \% n$ 。 因为 $hash$ 函数本身保证了映射的分布平均 和 一致性, 所以求余后的结果也符合我们的要求。 如下面图2.2, 我们可以用类似哈希表的方式来作为kvdb的节点分配规则:
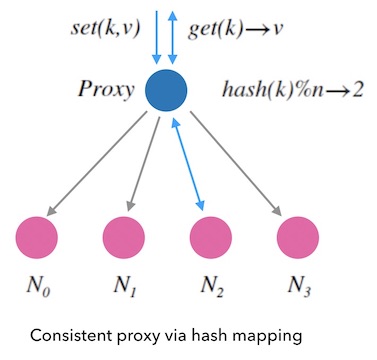
我们先把这种映射方式叫做「Mod-N哈希法」。
还记得哈希表的扩容吗? 当哈希表中插入元素越来越多的时候,哈希表就需要扩容。 这时候不得不重新申请一块新的连续内存,把所有的元素拷贝过去并进行重新映射(rehash)。
哈希表的扩容和重新映射都是全量进行的。 如果kvdb也模仿这种方式进行扩容, 就需要全量迁移数据,显然太麻烦了, 我们要寻找增量扩容的方式。
Mod-N哈希的扩容问题 ¶
下面,我们看下在前面提到的Mod-N哈希法的情况下, 新加一个节点或者移除一个故障节点会发生什么。
下图3.1中, 当新加一个节点 $N_4$ 时, 我们看到原本分配到 $N_2$ 的 $k$ 在扩容后会分配到 $N_1$。 对于一个kvdb来说,这意味着我们需要在扩容后把 $k$ 从 $N_2$ 迁移到 $N_1$ 才能继续提供服务。 否则的话,扩容后的读请求将映射到新的节点 $N_1$, 而导致读不到数据。
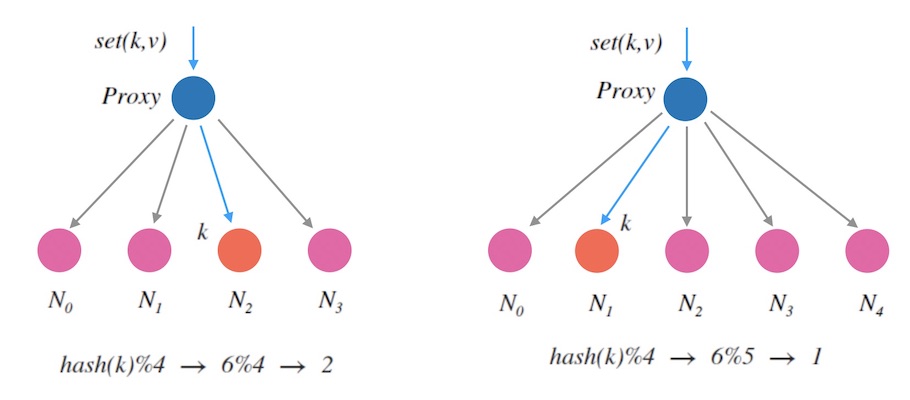
图3.1指出了,新增一个节点,会导致新映射和老映射的不一致。
对于删除一个节点的情况,也是类似的, 同样会导致新映射和老映射的不一致。 从下面图3.2中可以看到, 原本映射到 $N_2$ 的 $k$ 在缩容后映射到了 $N_0$, 也是不一致的:
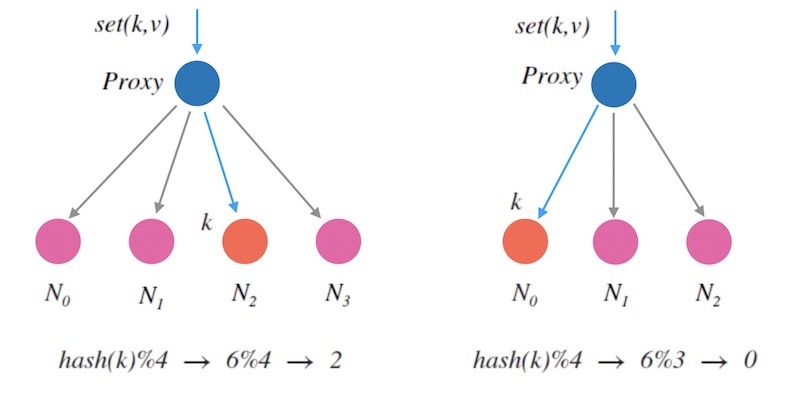
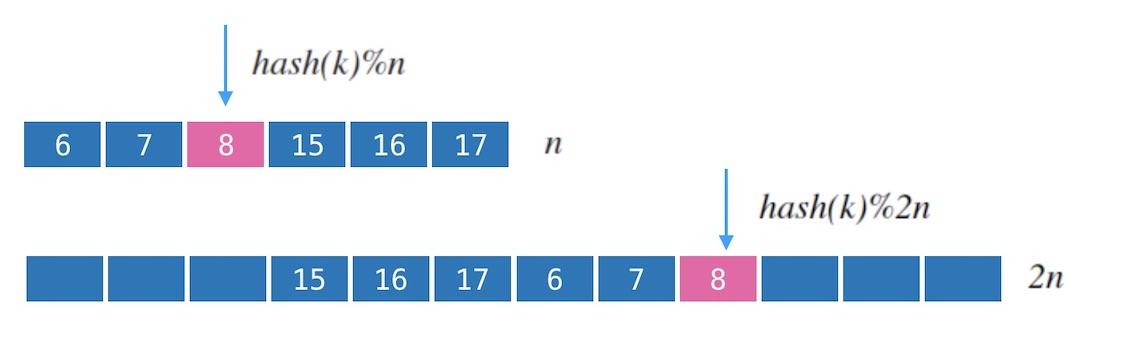
这种情况并不是特例, 而是会导致大面积的映射不一致。 下面的图3.3是4个节点和5个节点的情况下的哈希映射的对比图, 图中数字表示 $hash(k)$ 的值, 红色标记的数字则代表两种情况下的没有映射到同一个节点的值。 可以确定的是, 节点数变更后会导致大面积的映射不一致。
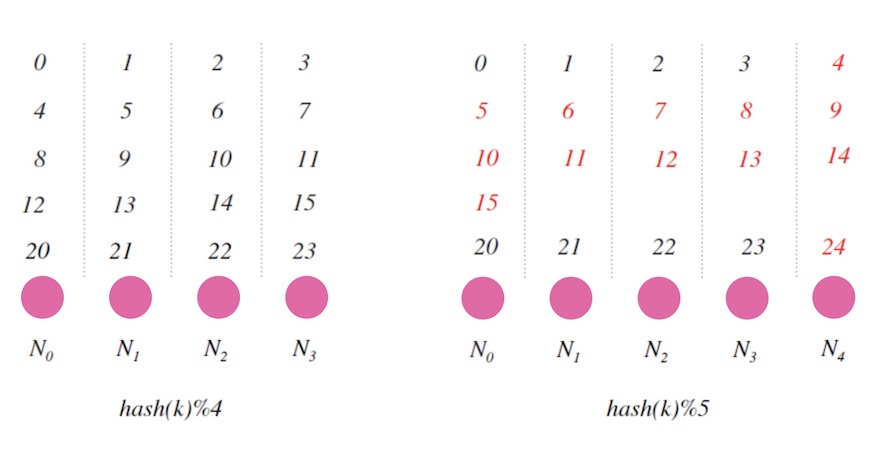
其实从数学上也可以简单地推出来, 只有当 $hash(k)$ 的结果对 $4$ 和 $5$ 的余数相等时才可能一致, 比如图中的 $0,1,2,3$, $20,21,22,23$,…, 其他情况都会不一致。
这样,我们对要寻找的映射函数的一致性要求更高了, 不仅要求对相同的 $k$ 的多次映射结果一致, 还要尽可能减少 $n$ 变化时带来的不一致性映射的变化。 构造这种映射的算法,就是一致性哈希算法。
一致性哈希算法 ¶
我们希望构造一种函数 $f(k, n) \rightarrow m$ 把字符串映射到 $n$ 个槽上:
- 它的输入是随机到来的字符串 $k$ 和 槽的个数 $n$.
- 输出是映射到的槽的标号 $m$ , $m < n$.
这个函数需要有这样的性质:
- 映射均匀: 对随机到来的输入 $k$, 函数返回任一个 $m$ 的概率都应该是 $1/n$ 。
- 一致性:
- 相同的 $k$, $n$ 输入, 一定会有相同的输出。
- 当槽的数目增减时, 映射结果和之前不一致的字符串的数量要尽量少。
更严格的、维基百科的定义是: 当添加一个槽时, 只需要对 $K/n$ 个字符串进行进行重新映射。
这个算法的关键特征在于, 不要导致全局重新映射, 而是要做增量的重新映射。
接下来将介绍三种一致性哈希算法:
– 毕「一致性哈希算法 - 问题的提出」。
本文原始链接地址: https://writings.sh/post/consistent-hashing-algorithms-part-1-the-problem-and-the-concept
