一致性哈希算法（二）- 哈希环法

本系列共分为四部分：

本文是第二部分。

哈希环法是最常用的、最经典的一致性哈希算法，也叫做割环法。这个算法易于理解、应用广泛（例如亚马逊的Dynamo），实现了最小化的重新映射。

一致性哈希环算法 ¶

具体的算法：

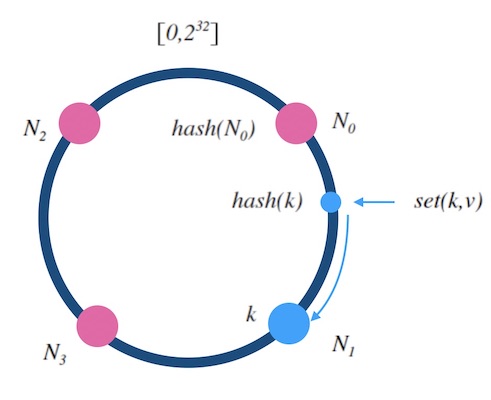
设 $hash(key)$ 是映射到区间 $\left[ 0,2^{ 32 } \right] $ 上的一个哈希函数。把区间首尾相连，形成一个顺时针增长的哈希环（如图5.1）。
将所有槽位(或者节点) $N_0, .., N_{n-1}$ 的标号 $0, …, n-1$ 依次作为 $hash$ 函数的输入进行哈希，把结果分别标记在环上。
对于关于 $k$ 的映射，求出 $z = hash(k)$ ，标记在环上：
1. 如果 $z$ 正好落在槽位上，返回这个槽位的标号。
2. 否则，顺时针沿着环寻找离 $z$ 最近的槽位，返回槽位标号。

我们接下来讨论下，当新增和删除槽位时，哈希环的表现如何。

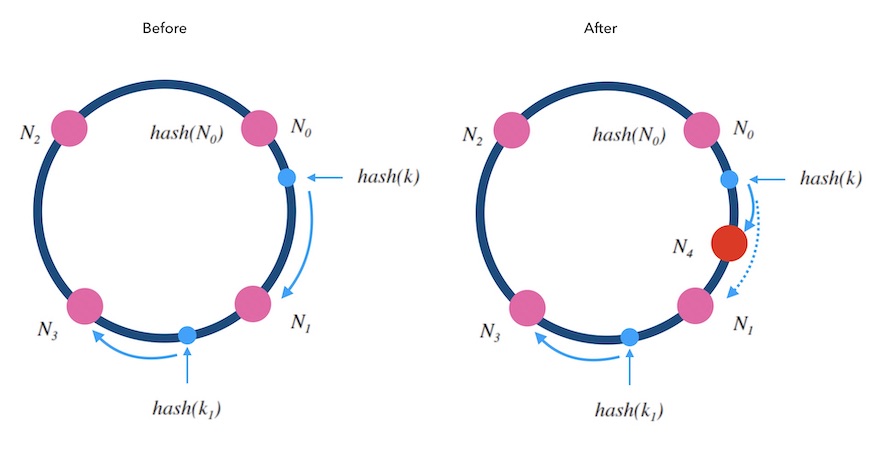
当往一个哈希环中新增一个槽位时，如下图5.2中，红色的 $N_4$ 是新增的槽位。可以看到 $k$ 从 $N_1$ 重新映射到了 $N_4$ , 而 $k_1$ 的映射结果不变。稍加分析可以知道，只有被新增槽位拦下来的 $k$ 的映射结果是变化了的。 新增槽位拦截了原本到下一节点的部分映射，其他槽位不受影响。对于kvdb的例子来说，顺时针方向的下一个节点 $N_1$ 需要迁移部分数据到新节点 $N_4$ 上才可以正常服务，其他节点不受影响。

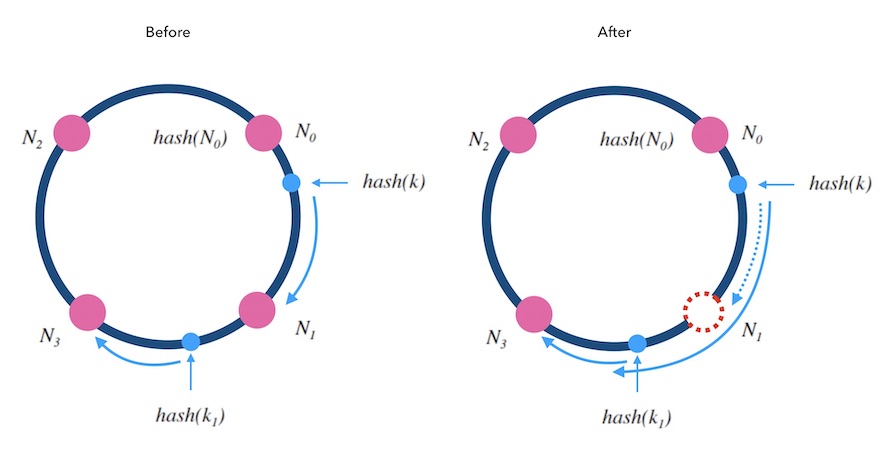
当从一个哈希环中移除一个槽位时，如下图5.3中，红色的 $N_1$ 是被删除的槽位。可以看到 $k$ 从 $N_1$ 重新映射到了 $N_3$，而 $k_1$ 的映射结果不变。 被删除槽位的映射会转交给下一槽位，其他槽位不受影响。 对于kvdb的例子来说，顺时针方向的原本映射到 $N_1$ 的请求会被转交到顺时针方向的下一个节点 $N_3$ 处理，所以需要迁移 $N_1$ 的数据到 $N_3$ 才可以正常服务。

哈希环做到了在槽位数量变化前后的增量式的重新映射，避免了全量的重新映射。

假设整体的 $k$ 的数量是 $K$ , 由于哈希映射的均匀性，所以，添加或者删除一个槽位，总会只影响一个槽位的映射量，也就是 $1/K$ , 因此，哈希环做到了最小化重新映射(minimum disruption)，做到了完全的一致性。

哈希环法的复杂度分析 ¶

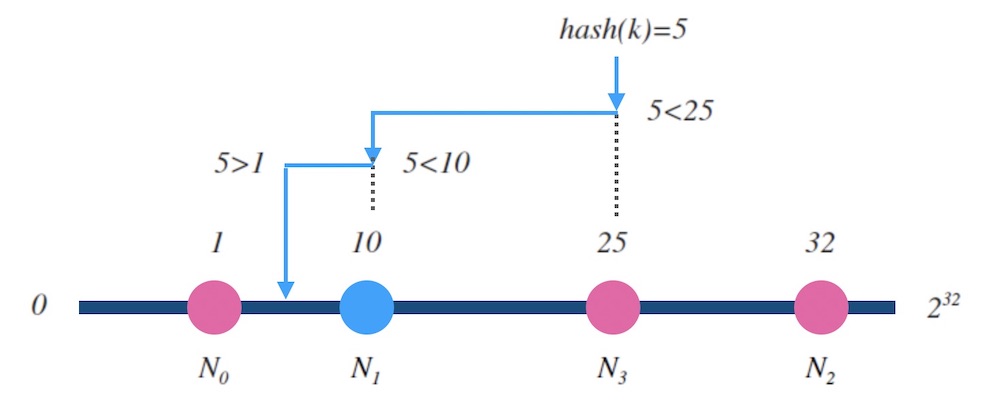
在技术实现上，实现哈希环的方法一般叫做 ketama 或 hash ring。核心的逻辑在于如何在环上找一个和目标值 $z$ 相近的槽位，我们把环拉开成一个自然数轴，所有的槽位在环上的哈希值组成一个有序表。在有序表里做查找，这是二分查找可以解决的事情，所以哈希环的映射函数的时间复杂度是 $O(log {n})$。

附注: 我对ketama做了简单的实现： C语言版本， Go语言版本。

对于空间复杂度，显然是 $O(n)$。

带权重的一致性哈希环 ¶

实际应用中，还可以对槽位（节点）添加权重。大概的逻辑是构建很多指向真实节点的虚拟节点，也叫影子节点。影子节点之间是平权的，选中影子节点，就代表选中了背后的真实节点。权重越大的节点，影子节点越多，被选中的概率就越大。

下面的图6.2是一个例子，其中 $N_0, N_1, N_2, N_3$ 的权重比是 $1:2:3:2$。选中一个影子节点如 $V(N_2)$ 就是选中了 $N_2$ 。

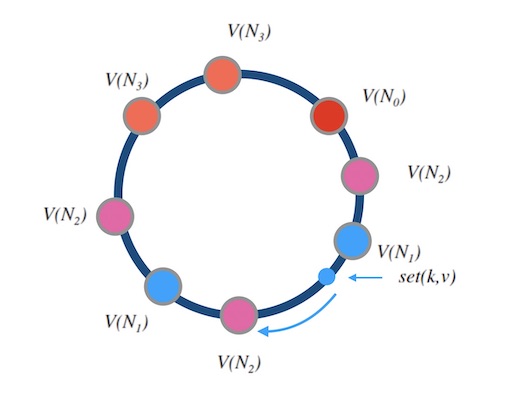
但是需要注意的是，权重的调整会带来数据迁移的工作。

哈希环上的映射分布的均匀性 ¶

实际应用中，即使节点之间是平权的，也会采用影子节点。比如，常用的ketama方法中，一般采用一个节点对应40个影子节点。原因是，节点越多、映射的分布越均匀， 采用影子节点可以减少真实节点之间的负载差异。

一致性哈希环算法的映射结果仍然不是很均匀^[1]：

With 100 replicas (“vnodes”) per server, the standard deviation of load is about 10%. Increasing the number of replicas to 1000 points per server reduces the standard deviation to ~3.2%.

意思是，当有100个影子节点时，哈希环法的映射结果的分布的标准差大约有 $10\%$。当影子节点增加到1000个时，这个标准差降到 $3.2\%$ 左右。

另外，和下一篇文章讨论的跳跃一致性哈希算法的均匀性对比，哈希环的表现也不是很好。

影子节点是一个绝妙的设计，不仅提高了映射结果的均匀性，而且为实现加权映射提供了方式。但是，影子节点增加了内存消耗和查找时间，以常用的ketama为例，每个节点都对应40个影子节点，内存的消耗从 $O(n)$ 变为 $O(40n)$ ，查找时间从 $O(logn)$ 变为 $O(log(40n))$ 。

一致性哈希环下的热扩容和容灾 ¶

回到kvdb的例子上来，对于增删节点的情况，哈希环法做到了增量式的重新映射，不再需要全量数据迁移的工作。但仍然有部分数据出现了变更前后映射不一致，技术运营上仍然存在如下问题：

扩容：当增加节点时，新节点需要对齐下一节点的数据后才可以正常服务。
缩容：当删除节点时，需要先把数据备份到下一节点才可以停服移除。
故障：节点突然故障不得不移除时，面临数据丢失风险。

如果我们要实现动态扩容和缩容，即所谓的热扩容，不停止服务对系统进行增删节点，可以这样做：

数据备份(双写)：数据写入到某个节点时，同时写一个备份(replica)到顺时针的邻居节点。
请求中继(代理)：新节点刚加入后，数据没有同步完成时，对读取不到的数据，可以把请求中继(replay)到顺时针方向的邻居节点。

下面的图7.1中演示了这两种规则：

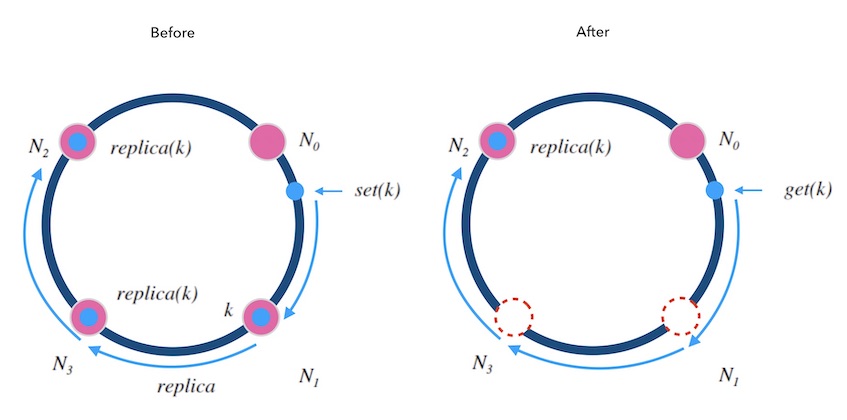
移除节点的情况：每一个节点在执行写请求时，都会写一个备份到顺时针的邻居节点。这样，当 $N_3$ 节点因故障需要踢除时，新的请求会交接给它的邻居节点 $N_2$， $N_2$ 上有 $k_1$ 的备份数据，可以正常读到。
新增节点的情况：对于新增节点的情况稍微复杂点，当新增节点 $N_4$ 时， $N_4$ 需要从邻居节点 $N_1$ 上同步数据，在同步仍未完成时，可能遇到的请求查不到数据，此时可以先把请求中继给 $N_1$ 处理, 待两个节点数据对齐后，再结束中继机制。
就像细胞分裂一样， $N_4$ 刚加入时可以直接算作时 $N_3$ 的一部分， $N_3$ 算作一个大节点，当数据对齐后， $N_4$ 再从 $N_3$ 中分裂出来，正式成为新节点。

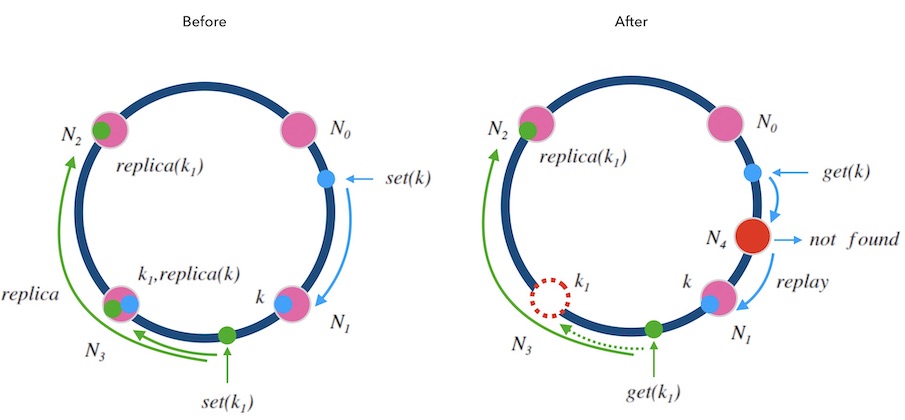
另外，可以备份不止一份。下面图7.2中演示了备份两次情况，每个写请求都将备份同步到顺时针方向的最近的两个节点上。这样就可以容忍相邻的两节点损失的情况，进一步提高了系统的可用性。

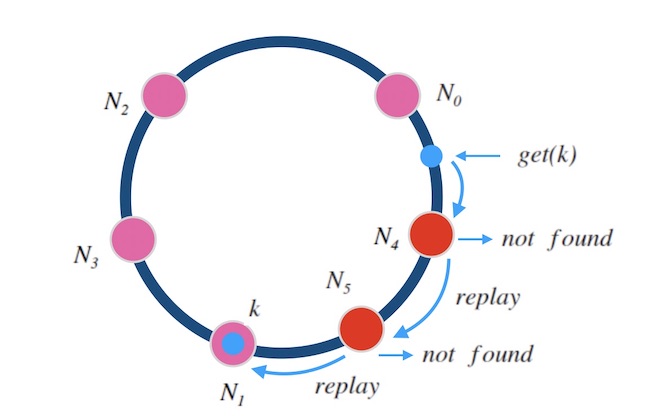
同样的，中继也可以不止一次。下面图7.3中演示了中继两次的情况，如果一个节点上查不到数据，就中继给下一个节点，最多两次中继，这样就可以满足同时添加”两个正好在环上相邻的”节点的情况了。

小结 ¶

哈希环法是经典的一致性哈希算法，避免了因槽位数量变化导致的全量重新映射，实现了最小化的重新映射。时间复杂度是 $O(log(n))$ ，空间复杂度是 $O(n)$，实际根据影子节点数量而乘上相应倍数。映射均匀性不是很优秀。热扩容和容灾的方式比较直观。

– 毕「一致性哈希算法 - 哈希环法」。

本系列的下一文章一致性哈希算法（三） - 跳跃一致性哈希法。

引用和脚注 ¶

Damian Gryski Consistent Hashing: Algorithmic Tradeoffs

本文原始链接地址： https://writings.sh/post/consistent-hashing-algorithms-part-2-consistent-hash-ring