一个构造单调序列问题的 DP 优化（slope trick）

源自蓝书《算阶》的一个 DP 问题，具有「思维难度极高，实现代码极短」的特点。

本文记录求解这个问题的一种叫做 slope trick 的冷门科技。

此问题在洛谷上的编号是 P2893：

给定一个长度为 $n$ 的序列 $A_i$，请构造一个长度也为 $n$ 的非严格单调（不降或者不升都可以）的序列 $B_i$ 使得 $S=\sum^{n}_{i=1} |A_i-B_i|$ 的值最小，输出这个最小的 $S$ 。

这个题目的意思，如下图所示，要构造一个要么非严格递增的、要么非严格下降的序列 $B$，它的各项和 $A$ 的对应元素的距离之和最小。洛谷上也有两道类似的变形题^[1] ^[2]。

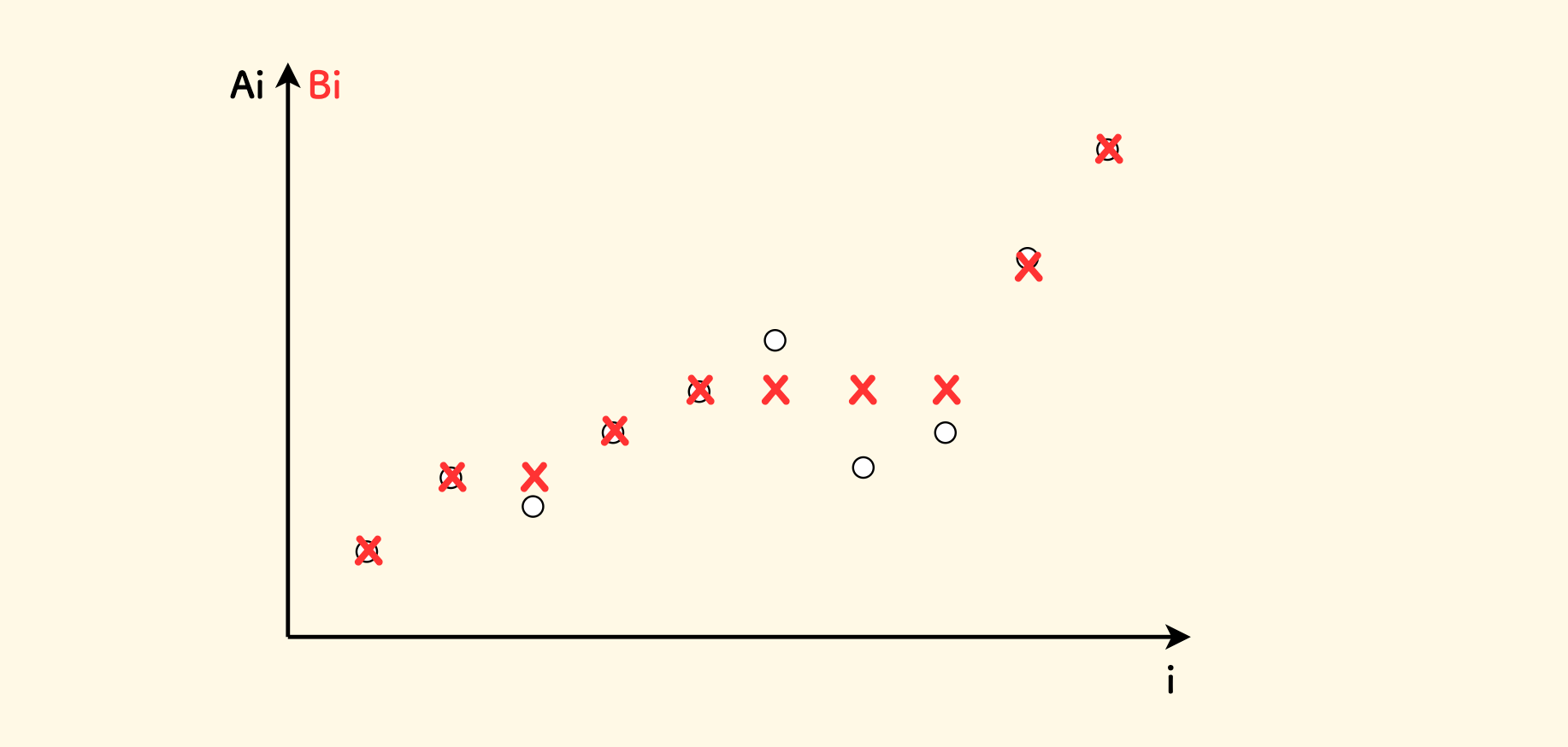
本文先说明 $O(n^2)$ 的线性 DP 解法，然后重点是 $O(n\log{n})$ 的 slope trick 方法。

题目要求非降和非增两种情况，可以分别求解，然后取最小答案。下面都只考虑构造非降的情况。

$O(n^2)$ 线性 DP 解法 ¶

《算阶》书上给出的是时间复杂度 $O(n^2)$ 的 DP 解法，它基于一个关键的引理：

在满足 $S$ 最小化的前提下，一定存在一种构造序列 $B$ 的方案，使得 $B$ 中的数值都在 $A$ 中出现过。

但是书中关于这个引理的证明^[3]我没看懂。我看了一些题解，也鲜有证明其原因的。

不过，这个引理的正确性可以从另一个视角看到，后面会说到。

假设 $f(i, x)$ 表示完成前 $i$ 个数的构造且以值 $B_i=x$ 结尾的时候，$S$ 的最小值，容易写出转移方程（注意现在是求非降的情况）：

\[f(i, x) = \min_{0 \leq k \leq x} \left\{ f(i-1, k) + |x - A_i| \right\}\]

其伪代码实现大概如下：

初步分析的 C++ 实现

memset(f, 0x3f, sizeof f);     // +inf，因为要取最小值
memset(f[0], 0, sizeof f[0]);  // i=0 时取 0
int m = *max_element(A + 1, A + n + 1); // A 的最大元素值
for (int i = 1; i <= n; i++) {
  for (int x = 0; x <= m; x++) {
    for (int k = 0; k <= x; k++) {
      f[i][x] = min(f[i][x], f[i - 1][k] + abs(x - A[i]));
    }
  }
}
// 答案是 i=n 时可取到的最小值
return *min_element(f[n], f[n] + m + 1);

根据引理，可以先把 $A$ 序列的值离散化处理，假设 $a$ 是离散化后的数列，它是有序且去重的，转移方程可以用下标表示了：

\[f(i, j) = \min_{1 \leq k \leq j} \left\{ f(i-1, k) + |a_j - A_i| \right\}\]

离散化后，第 2、3 层循环可以降低到 $O(n)$：

离散化处理后的 $O(n^3)$ C++ 代码

// 离散化：a 是有序且去重的
for (int i = 1; i <= n; i++) a[i] = A[i];
sort(a + 1, a + n + 1);
int m = unique(a + 1, a + n + 1) - (a + 1);

// DP 求解, 并用索引代替值 x 表示
memset(f, 0x3f, sizeof f);     // inf
memset(f[0], 0, sizeof f[0]);  // i=0
for (int i = 1; i <= n; i++) {
    for (int j = 1; j <= m; j++) {
        for (int k = 1; k <= j; k++) {
            // a 是有序的，k 此时只需要 <=j
            f[i][j] = min(f[i][j], f[i - 1][k] + abs(a[j] - A[i]));
        }
    }
}
// 答案是 i=n 时可取到的最小值
return *min_element(f[n], f[n] + n + 1);

再进一步地，内两层循环可以采用类似 LCIS 问题的优化方式，整体进一步优化到 $O(n^2)$。

思路是，把 $f(i, j)$ 的推导过程看做以 $i$ 为行、$j$ 为列的 DP 填表过程。只需要维护一个变量 $mi$，来同步跟进上一行 $f_{i-1}$ 中满足 $\leq j$ 的 dp 最小值即可。这个转移优化的根本原因是，最内层的取最值可以和第二层线性地齐头并进。这样，第 2 、3 层循环可以合并成 1 层。

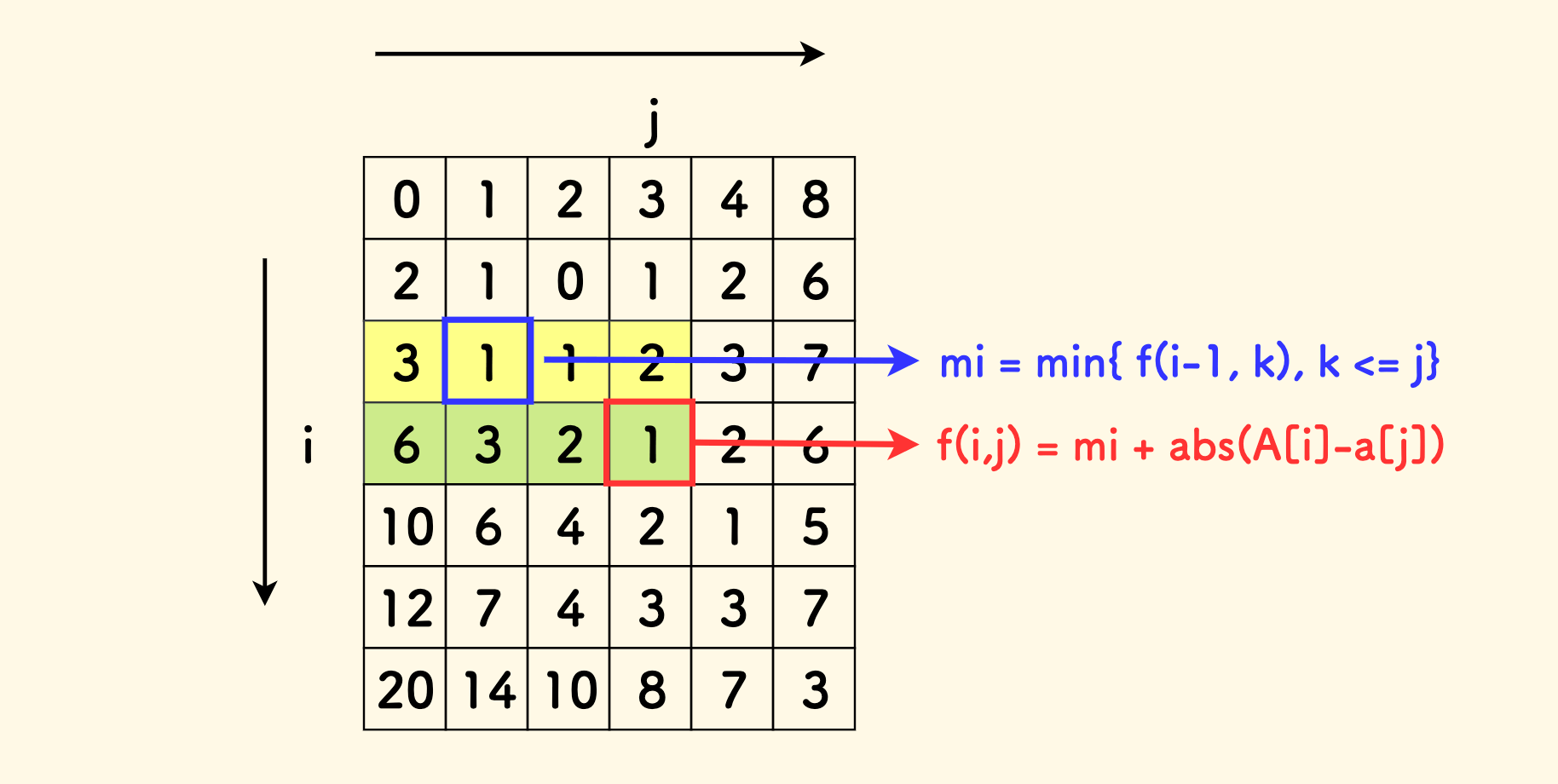
优化转移后的 $O(n^2)$ C++ 代码

for (int i = 1; i <= n; i++) {
    int mi = 0x3f3f3f3f;
    for (int j = 1; j <= m; j++) {
        // mi 同步跟进上一行 f[i-1] 中 <=j 的最小值
        mi = min(mi, f[i - 1][j]);
        f[i][j] = mi + abs(a[j] - A[i]);
    }
}

至此，$O(n^2)$ 的线性 DP 解法说明完毕。

洛谷 P2893 的 $O(n^2)$ 完整 C++ 代码实现 - github

此外，这个问题还有一种「可并堆」^[4] 的做法，不过我也没能理解其正确性。

Slope trick $O(n\log{n})$ 解法 ¶

这个解法讲的会比较长，分五个部分：

slope trickable 的概念
用堆描述一个 slope trickable 凹函数
题目中的 $f_i(x)$ 是 slope trickable 的凹函数
追踪答案的变化
延伸 - 输出一个非降的序列 $B$

slope trickable 的概念 ¶

slope trick 技巧可能最早来自于问题 codeforces 713C。下面的说明，参考了 codeforces 这一篇文章。

简而言之，是一种可以用优先级队列/堆来维护分段凸函数在合并过程中的拐点和斜率变化的方法。

读起来十分绕口，再简单一些说，就是「堆动态描述斜率变化」。

如果一个函数满足下面的性质，就认为是可以用 slope trick 来描述的：

函数是连续的。
函数是分段的，每一段是斜率为整数的线性函数。
是一个凸函数或者凹函数。或者说，函数的斜率是单调非增或单调非降的。

这种函数可以叫做 slope trickable 的函数，这种函数有一个很优秀的关于合并的性质：

两个凹凸方向一致的 slope trickable 函数 $f(x)$ 和 $g(x)$ 的合并后的函数 $h(x) = f(x) + g(x)$ 也是 slope trickable 的。
合并后的拐点集合是 $f$ 和 $g$ 各自的拐点集合的并集。

这个性质也容易理解，根据求导法则 ^[5]，可以知道 $h’ = f’ + g’$，再加证明即可。

由于本题目的特点是求最小值，下面主要研究凹函数，道理对于凸函数是应该是类似的。

比如，函数 $f=|x-2|$ 和 $g=|x-4|$ 都是 slope trickable 的凹函数，合并后的 $h = f + g$ 也是一个凹函数。而且可以看到，合并后的拐点 $\{2,4\}$ 是由 $f$ 和 $g$ 的拐点合并而成（拐点是说的横坐标 $x$ 的取值）。

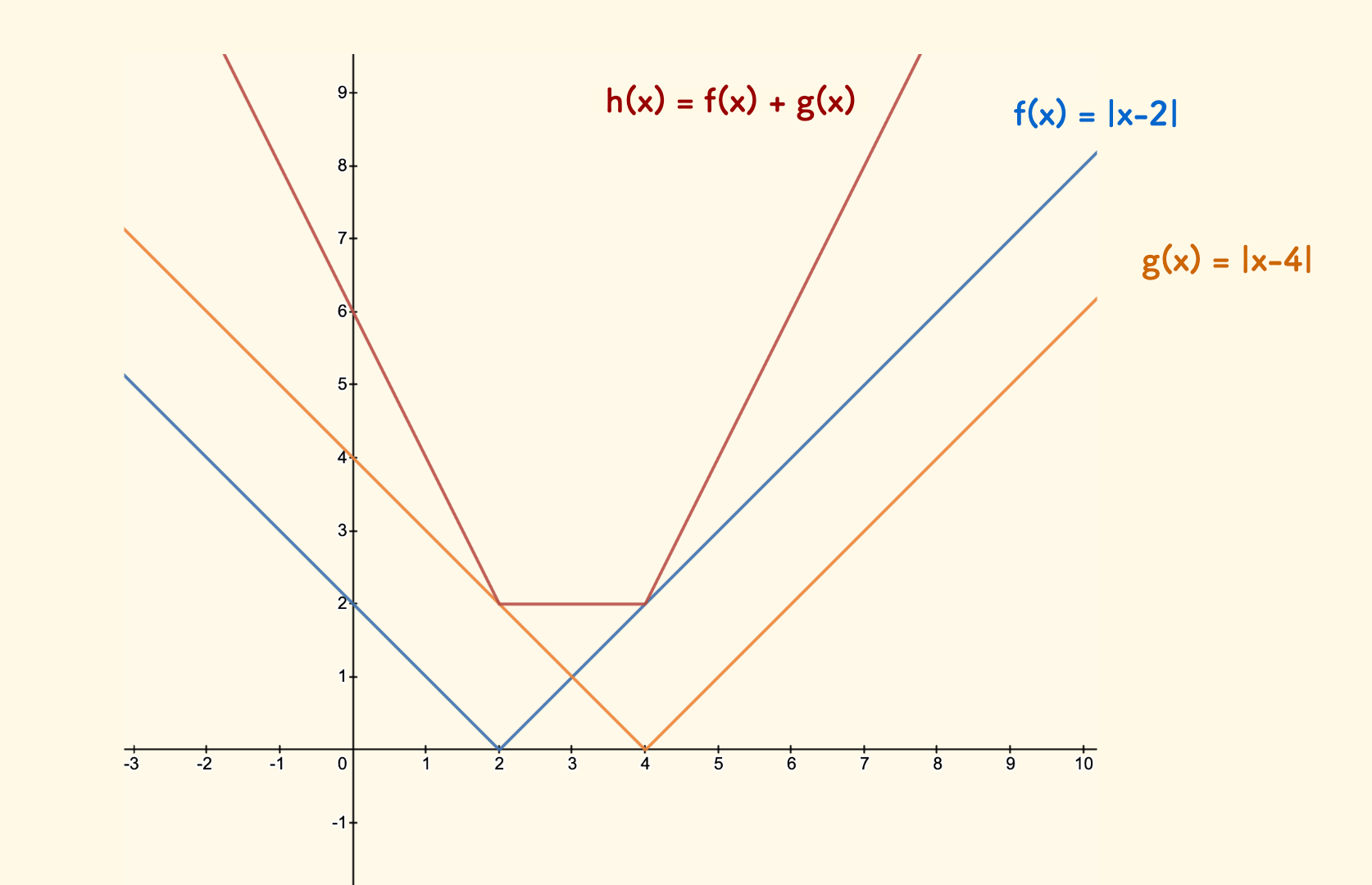
用堆描述一个 slope trickable 凹函数 ¶

事实上，本题目的 $f$ 函数是一个前缀最小值凹函数（就是只有左边下坡、没有右边上坡），但是出于一般性说明，本小节先考虑更通用的两边都有坡的凹函数为例子，将说明可以用堆来描述一个 slope trickable 的凹函数。

下面考虑一个不断演进的示例函数 $g_i(x)$，其中 $g_0(x) = 0$ ：

\[g_i(x) = g_{i-1}(x) + |x - A_i|\]

将考察这个函数的最小值 $\min{g_i(x)}$ 的演进过程。

首先，可以数学归纳法论证每一个函数 $g_i(x)$ 是一个满足 slope trickable 定义的凹函数，而且它的拐点集合是 $\{A_1,A_2,…,A_i\}$，证明省略。

随着 $i$ 的递进，看一下 $g_i(x)$ 函数会发生什么样的变化，注意函数的和的导数是导数的和^[5]：

当 $x \leq A_i$ 时，斜率的变化是 $-1$。
\[\begin{split} g_i(x) &= g_{i-1}(x) + A_i - x \\ \rightarrow g_i' &= g_{i-1}' -1 \end{split}\]
当 $x > A_i$ 时，斜率的变化是 $+1$。
\[\begin{split} g_i(x) &= g_{i-1}(x) + x - A_i \\ \rightarrow g_i' &= g_{i-1}' +1 \end{split}\]

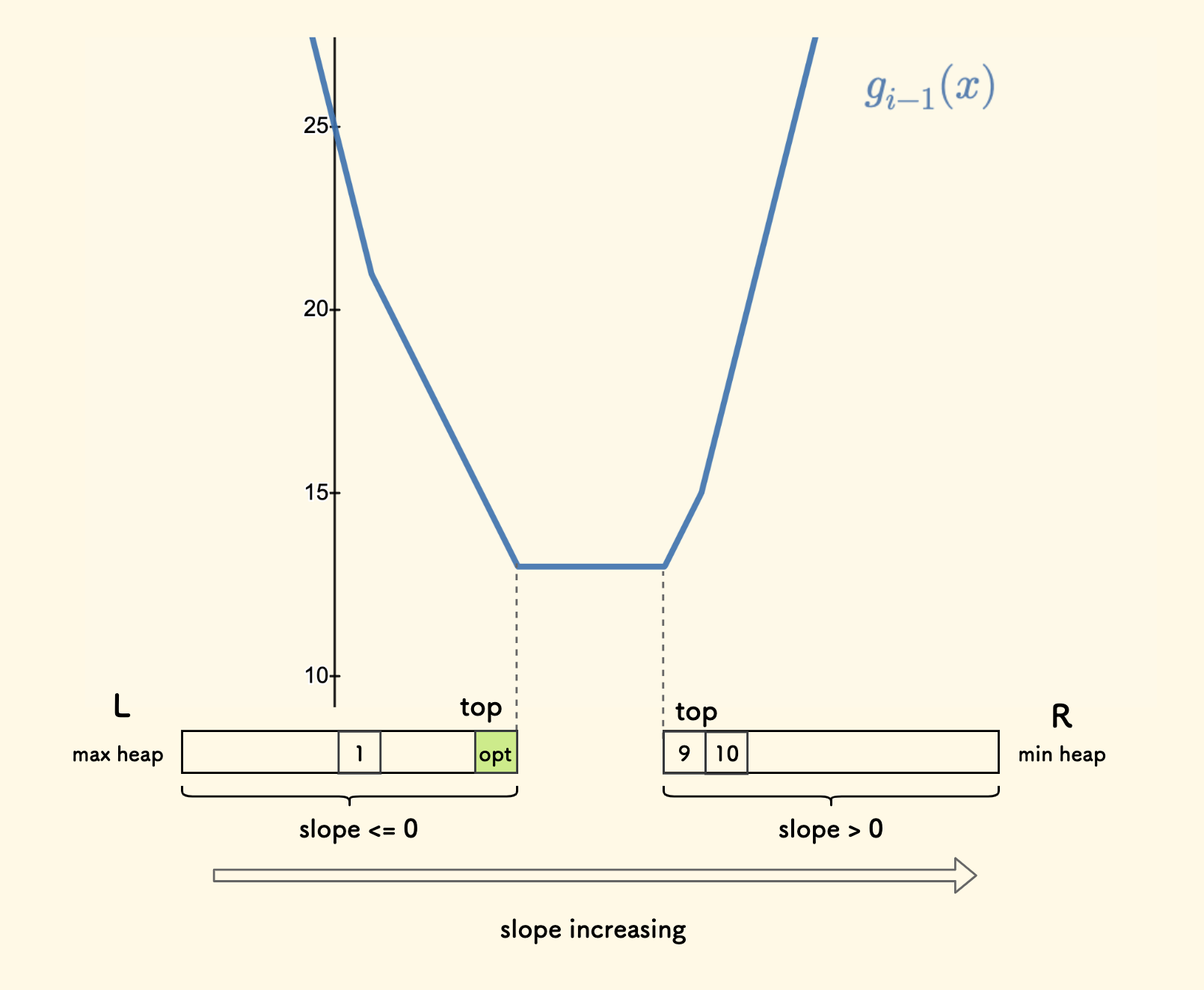
下面是示例图，展示了函数 $g_{i-1}$ 演进到 $g_i$ 的变化情况，根据新加入的拐点 $A_i$ 和原来的最优点 $opt$ 的位置关系分为左右两个图，可以发现：

$A_i$ 左边的下降段，斜率 $-1$，会变的更陡。
$A_i$ 右边的上升段，斜率 $+1$，会变的更陡。
当 $A_i \leq opt$ 时，它右边原来斜率为 $-1$ 点，会成为新的最优点。
当 $A_i > opt$ 时，它左边原来斜率为 $+1$ 点，会成为新的最优点。

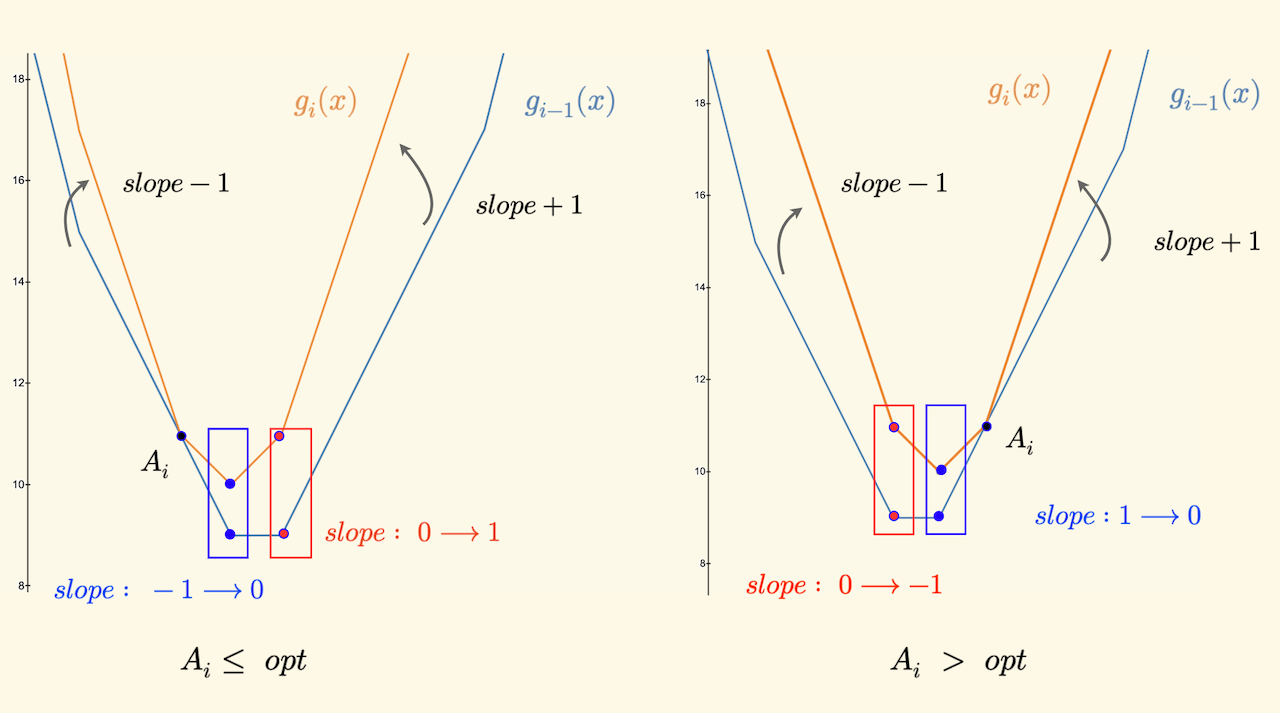
接下来，尝试用数据结构来描述这一变化。

可以用有序表，确切地说，可以用两个堆来存储拐点。

具体来说：

大根堆 L 来存储 $slope \leq 0$ 的拐点（指横坐标 $x$），斜率表示为其在堆中的深度的相反数。
小根堆 R 来存储 $slope > 0$ 的拐点（指横坐标 $x$），斜率表示为其在堆中的深度。
由于采用堆的深度来表示斜率，所以如果两个拐点斜率之差 $>1$ 的话，则插入多份拐点，确保堆中相邻元素斜率之差恰好为 $1$。

可以知道：

最优点 $opt$ 在 L 堆顶，斜率为 $0$ 。
从 L 的堆底到 R 的堆底，斜率以步长 $1$ 严格递增。

现在考虑，插入一个新的拐点 $A_i$ 时，应该如何维护两个堆？

因为函数 $|x-A_i|$ 在拐点 $A_i$ 的斜率变化是 $-1$ 到 $+1$ 变化量是 $2$，所以要考虑加入两个 $A_i$ 到堆中，以确保堆中相邻元素斜率之差恰好为 $1$。

先考虑 $A_i <= opt$ 的情况，此时应该放两个 $A_i$ 到 L 堆中，验证下各段斜率的变化：

原来的最优点 $opt$ 的斜率从 $0$ 变为 $+1$，应该弹出，并放入 R 中。
进而地，R 中的斜率都会 $+1$，符合预期。
在 L 堆中，$A_i$ 右边弹出了堆顶元素：
1. $A_i$ 右边的拐点在堆中的深度都会减小，斜率都会 $+1$，符合预期。
  特殊地，原来次堆顶的元素会成为新的最优点。
2. 但是同时插入了两个 $A_i$，所以 $A_i$ 左边的深度会 $+1$，也就是斜率会 $-1$，也符合预期。

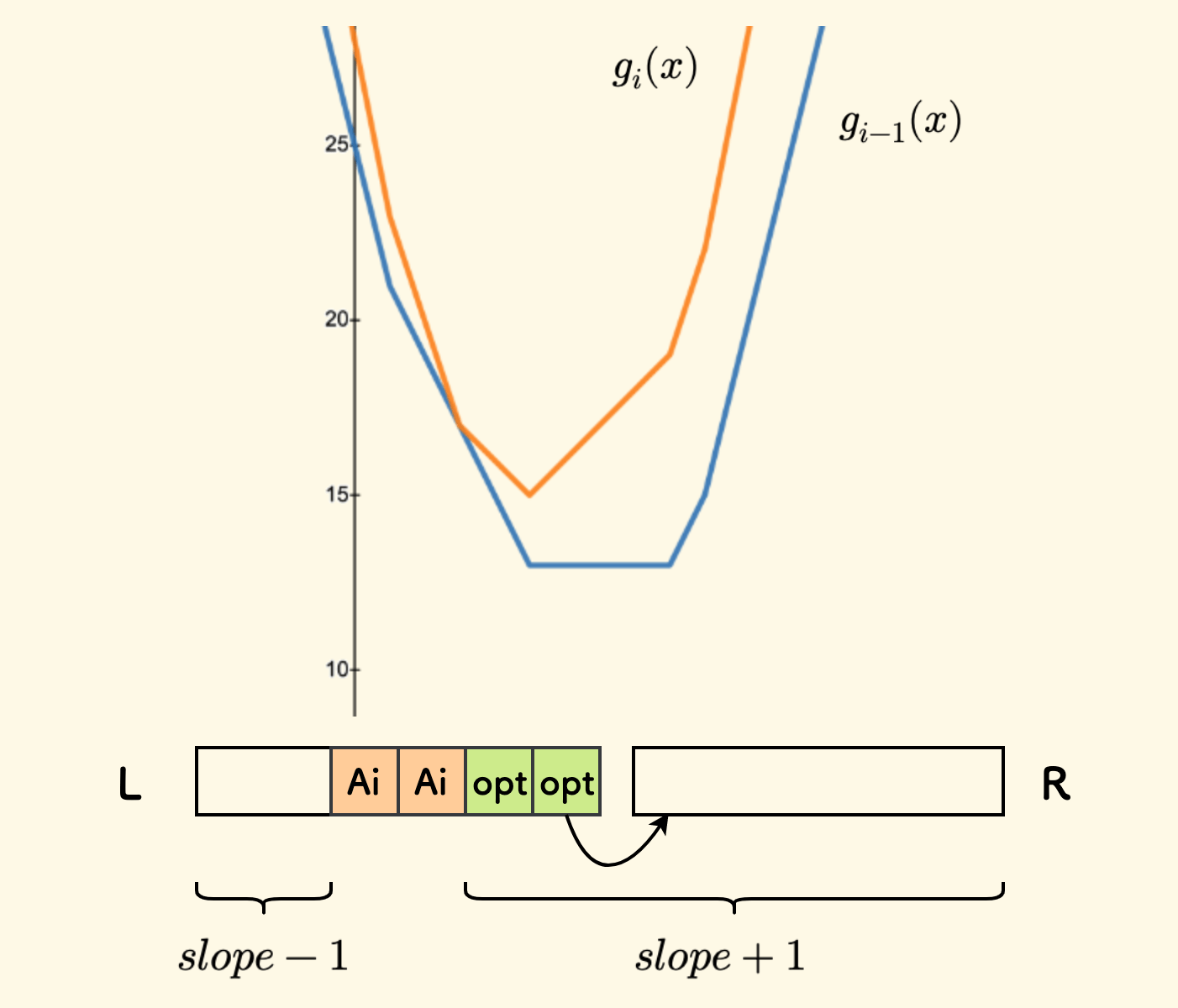
对于 $A_i > opt$ 的情况，是类似的，不再展开讨论。

总之，现在已经找到了一种方法，可以用两个堆来描述满足 slope trickable 定义的分段凹函数的动态合并过程。

其中的关键点：

可以用一个大根堆 L 和小根堆 R 来维护凹函数合并过程中的拐点和斜率的变化。
两个堆中的元素的斜率是按步长 $1$ 严格递增的，如果斜率变化超过 $1$，就要存多份。
凹函数的最优决策点始终保持在 L 堆顶。

题目中的 $f_i(x)$ 是 slope trickable 的凹函数 ¶

现在终于回到题目中最开始的 DP 方程，即 $f(i, x)$ 表示完成前 $i$ 个数的构造且以值 $B_i=x$ 结尾时 $S$ 的最小值：

\[f(i, x) = \min_{0 \leq k \leq x} \left\{ f(i-1, k) + |x - A_i| \right\}\]

对每一个 $i$，构造一个函数 $q_i(x)$：

\[q_i(x) = f_{i-1}(x) + |x - A_i|\]

而 DP 函数 $f_i(x)$ 其实就是：$\min_{0 \leq k \leq x} \{ q_{i}(k) \}$，即 $f_i(x)$ 是 $q_i(x)$ 的前缀最小值函数。

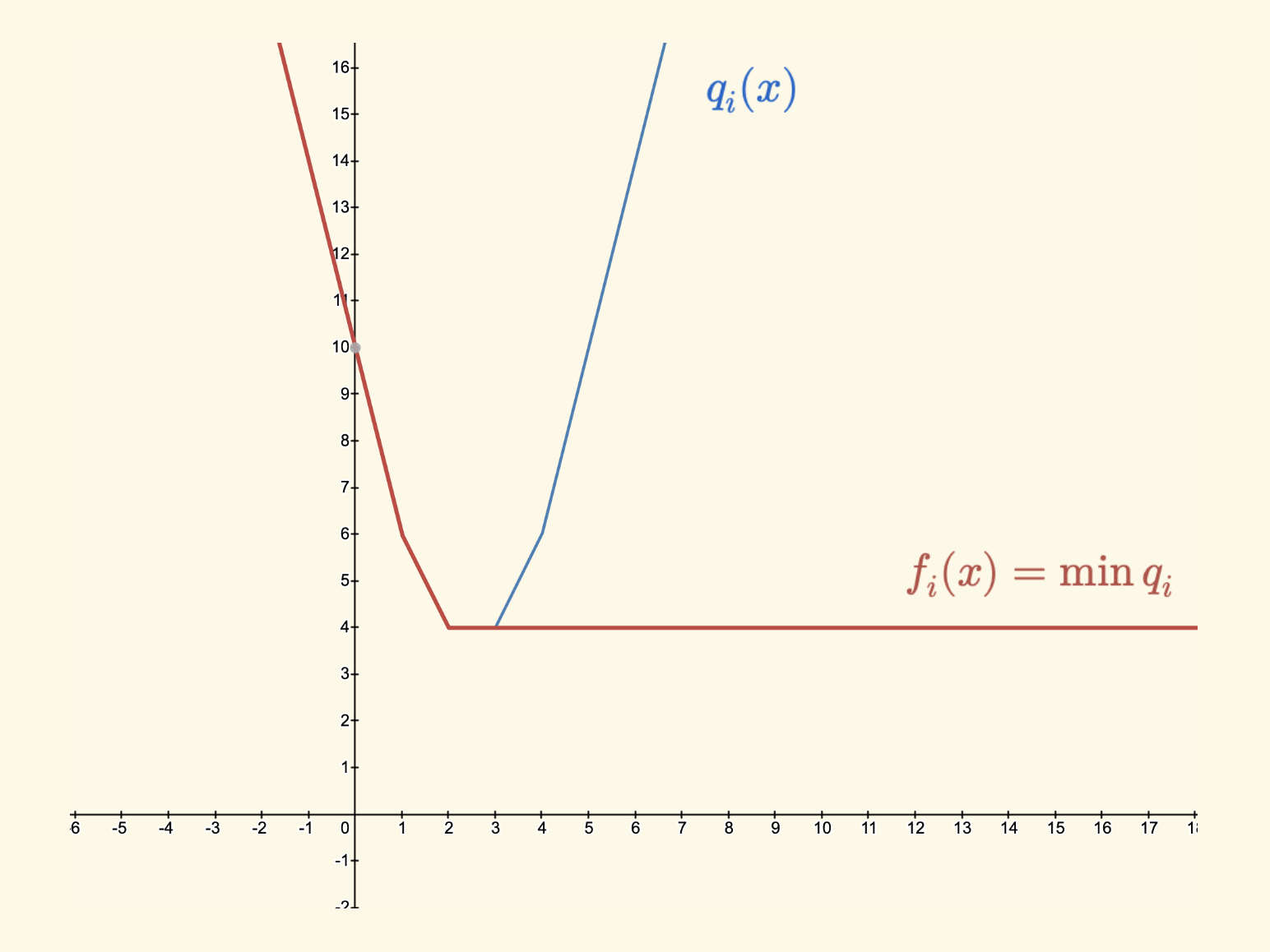
可以数学归纳知道，$q_i(x)$ 和 $f_i(x)$ 都是 slope trickable 的凹函数，而且拐点全部在集合 $\{A_1, A_2,…, A_i\}$ 中，同时说明了前面 $O(n^2)$ DP 中引理的正确性。

数学归纳证明 $f_i(x)$ 和 $q_i(x)$ 都是满足 slope trickable 定义的凹函数

首先，当 $i=1$ 时，显然 $q_1=|x-A_1|$ 是成立的，拐点集合是 $\{A_1\}$。
考虑 $i$ 的情况，如果 $q_{i-1}(x)$ 是满足 slope trickable 的凹函数，那么其前缀最小值函数 $f_{i-1}(x)$ 也会满足此性质。 $q_i(x)$ 就是 $f_{i-1}(x)$ 和凹函数 $|x - A_i|$ 合并而来，那么 $q_i$ 也满足，每次合并会添加一个新的拐点 $\{A_i\}$。

根据前面的讨论，$f_i(x)$ 的情况会更简单，只需要维护左边的大根堆 L 即可：

大根堆 L 来维护 $f_i(x)$ 函数的拐点和斜率的变化。
最优决策点保持在 L 的堆顶。
堆 L 的维护操作是：每次加入两个 $A_i$，并弹出一次堆顶丢弃掉。

追踪答案的变化 ¶

考虑下题目中答案的变化情况，假设 $i-1$ 的时候的最优点在 $x=opt_{i-1}$ 处：

当 $A_i > opt_{i-1}$ 时，最优点是 $A_i$，此时 $ans$ 无变化。
L 堆中对应的操作是：推入 2 个 $A_i$，成为新的堆顶，再弹出堆顶。
效果等价于仅推入 1 个 $A_i$。 $A_i$ 左侧的拐点在堆中深度 $+1$，斜率则会 $-1$，坡线会变陡。
当 $A_i \leq opt_{i-1}$ 时，考虑 $i$ 的情况：

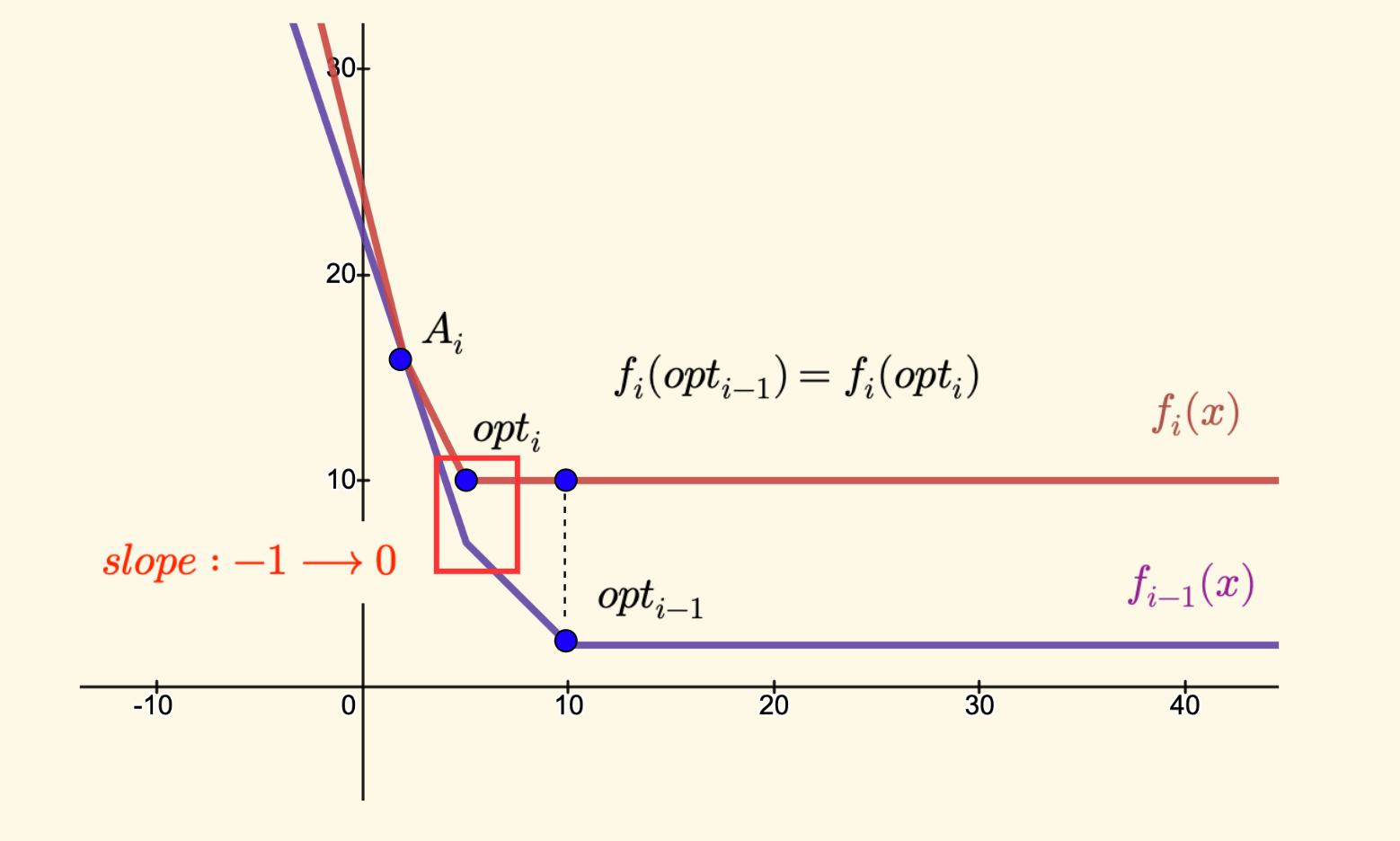
原来斜率为 $-1$ 的点（次堆顶的元素）会成为新的最优点 $opt_{i}$，也就是 $opt_{i-1}$ 的左侧最近的拐点。

而且可以知道原来的最优点 $opt_{i-1}$ 在当前新的函数 $f_i(x)$ 中的取值也是当前最小函数值：

\[\begin{split} f_i(opt_i) &= f_i(opt_{i-1}) \\ &= \min{f_{i-1}(opt_{i-1})} + |opt_{i-1} - A_i| \\ &= f_{i-1}(opt_{i-1}) + opt_{i-1} - A_i \end{split}\]

也就是说，答案的递推式是：$ans = ans + L.top() - A_i$ 。

接下来，可以发现递推式其实可以适合 1 和 2 两种情况。

尝试先入堆，再查看堆顶：

q.push(A[i]);
q.push(A[i]);
ans += q.top() - A[i];
q.pop();

验证下 $A_i > opt_{i-1}$ 的情况，因为此时堆顶一定是更大的 $A_i$，所以：
\[\begin{split} ans &= ans + L.top() - A_i \\ &= ans + A_i - A_i \\ &= ans \end{split}\]
答案也符合这个递推式，无变化。
验证下 $A_i \leq opt_{i-1}$ 的情况，先压入堆中，堆顶并不会被替换，因为 $A_i$ 不超过堆顶：
\[\begin{split} ans & = ans + L.top() - A_i \\ & = ans + opt_{i-1} - A_i \end{split}\]
答案仍然正确。

综合一下，就是说，先推入堆，再计算答案，可以用统一的答案递推式。

最终步骤则是：

先把两个 $A_i$ 压入堆中。
再计算 $ans = ans + L.top() - A_i$。
弹出堆顶，维护 L 堆的性质。

用代码来描述如下：

int ans = 0;
priority_queue<int> q;
for (int i = 1; i <= n; i++) {
    q.push(A[i]);
    q.push(A[i]);
    ans += q.top() - A[i];
    q.pop();
}

总体时间复杂度是 $O(n\log{n})$。

另外，注意回到原题目，还要反转数组求一下构造非增数列 $B$ 的情况，然后取两种情况的最小答案。

洛谷 P2893 的 $O(n\log{n})$ 完整 C++ 代码实现 - github

输出一个非降数列

最后，如何输出一个满足要求的非降数列呢？

需要提醒的是，注意 $B_i$ 的取值不应简单赋值为 $L.top()$，因为最优点会倒退。

要保证最终 $i=n$ 时的整体最优，所以一定有 $B_n = opt_n$。

从后向前推，当 $i=n-1$ 时，分类讨论：

如果 $opt_{n-1} \leq opt_n$，直接取 $B_{n-1} = opt_{n-1}$ 即可。
如果 $opt_{n-1} > opt_n$，说明来自情况 2，导致了最优点倒退。
由于要保证非降，必须要 $ B_{n-1} \leq B_n$，那么：
1. $B_{n-1}$ 至多为 $B_n$。
2. $B_{n-1}$ 应该尽量靠近 $opt_{n-1}$，而左侧这一段斜率为 $-1$，$opt_n$ 为左侧最近拐点。
综合来看，此时只能取 $\min{\{opt_{n-1}, opt_n\}}$。

依此倒序类推，伪代码实现大概如下：

priority_queue<int> q;
for (int i = 1; i <= n; i++) {
    q.push(A[i]);
    q.push(A[i]);
    B[i] = q.top();  // opt(i)
    q.pop();
}
for (int i = n - 1; i; i--) B[i] = min(B[i], B[i + 1]);

P4331 问题 ^[1] 是一个类似的问题，只不过要求严格递增的数列 $B$，要动一动脑筋。

洛谷 P4331 的完整 C++ 代码实现 - github

结尾语 ¶

这道问题果然非常考验思维，代码又极其简短。

slope trick 总归是一个冷门的知识，神奇的是斜率竟然和堆联系在了一起。

妙啊~~ ！

（完）

脚注 ¶

洛谷 P4331：要求构造严格递增的序列 $B$。
洛谷 P4597：用每次 $+1$ 或 $-1$ 的操作把 $A$ 变成这样的 $B$，求最小操作次数。
《算阶》书中给出的引理的证明 - 数学归纳法
首先，$n=1$ 的时候显然成立。
假设对 $n=k-1$ 时成立，此时构造的序列是 $B_1 .. B_{k-1}$：
1. 如果 $B_{k-1} \leq A_k$，直接令 $B_k = A_k$ 即可。
2. 否则，要么令 $B_k = B_{k-1}$，此时命题仍成立，要么存在一个 $j$ ，令 $Bj,B{j+1},…,B_k$ 为同一个值 $v$。考虑到中位数的性质，取 $A_j,A_{j+1}…,A_k$ 的中位数 $mid$：
  1. 如果 $mid \geq B_{j-1}$，则有 $v=mid$ 。
  2. 否则，应该有 $ v = B_{j-1}$。
  无论哪种情况，$B1..B_k$ 中的数都在 $A$ 中出现过。
这个引理的证明，我不懂的地方在于第二点：
1. 取前面一段的 $A$ 的中位数，把 $B$ 这一段全部替换成它，一定是最优的吗？这一段 $A$ 并不一定单降。
2. 这样的 $j$ 一定存在吗？
3. 中位数仍不满足的时候，继续取 $B$ 这一段的前一个元素就是最优的吗？
如果读者朋友有合理的解释，欢迎评论区指点迷津。
一种「可并堆」维护中位数的做法
一种做法维护中位数的可并堆的做法，发现于 P4331 的题解区，但是我没有理解其正确性。
大致思路是：先考虑每个单调的分段，然后再合并的做法。
在两种特殊情况下，存在如下的事实（这两点是容易理解的）：
1. 对于 $A$ 中非降的一段，直接取每一项 $B_i = A_i$，这一段的 $S$ 最优。
2. 对于 $A$ 中单调递减的一段，只能取 $B$ 这一段的每一项为这一段的 $A$ 的中位数。
这类解法的大概的思路是：
1. 先把非降的所有段，设置 $B_i = A_i$。
2. 然后把所有递减段，取这一段的中位数，如果此中位数不能和前面的 $B$ 构成上升，就继续向前扩展 $A$ 的这一段再对其求中位数。
3. 最终会形成一个非降的 $B$。
但是这一类做法，从题解上，没有其正确性分析。
导数的求导法则 - 维基百科
参考资料：《Slope trick explained》 by Kuroni - codeforces

本文原始链接地址： https://writings.sh/post/slope-trick-mono-sequence