链表 - 经典算法问题总结

本文总结链表的几个经典算法问题，包括：

回文链表
区间反转
链表分割
链表合并
链表排序
链表相交
链表查环

本文内容较多，需要静心阅读。

以下所有的代码将基于以下的单链表结构：

单链表结构 - C 语言

struct Node {
    int v;  // 数据
    struct Node *next;
};

回文链表 ¶

问题：判断一个单链表是否回文。

例如，3->1->1->3 是一个回文链表。

leetcode 题目 - 回文链表

这个问题的方法有许多种：

将链表节点全部入栈，然后出栈和原链表比较。
拷贝一份原链表，反转后和原链表进行比较。
将链表拷贝到数组，判断数组是否回文。

这里只讲一个空间复杂度为 $O(1)$ 的方法，需要修改输入的链表。

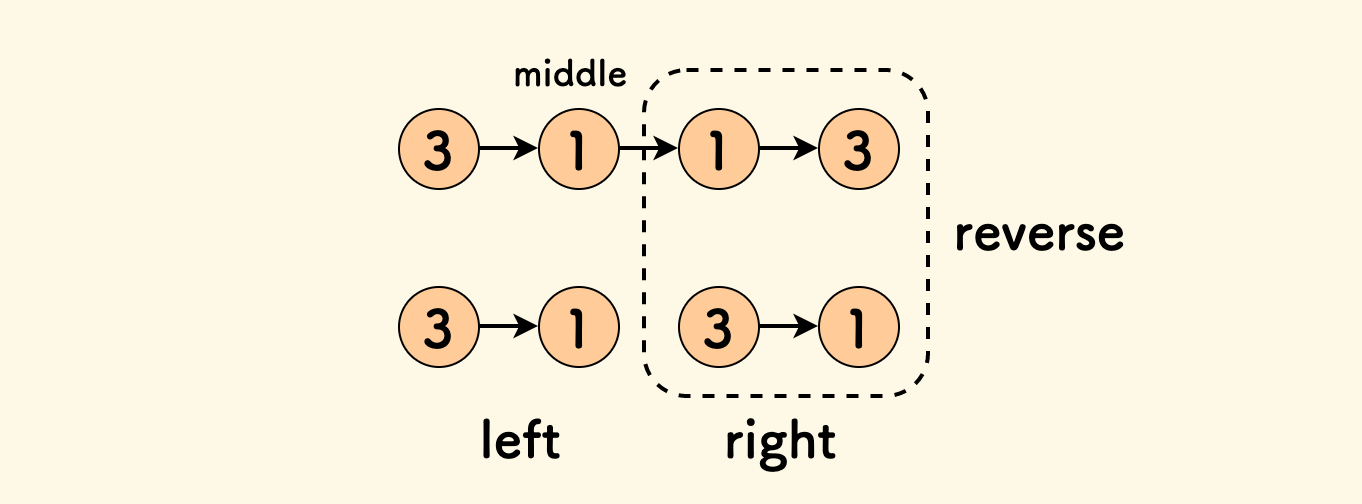
其思路是：

找出链表的尾巴和中点。
反转右边的一半。
比较链表的左边和反转后的右边。

判断回文链表 - C 语言实现

// 找出链表中间节点
// 例：abcd => b , abcde => c
struct Node *Middle(struct Node *node) {
    struct Node *slow = node;
    struct Node *fast = node;
    struct Node *prev = NULL;

    while (fast != NULL) {
        // 每人一步
        fast = fast->next;
        prev = slow;
        slow = slow->next;
        // fast 多走一步
        if (fast != NULL) fast = fast->next;
    }
    return prev;
}

// 反转链表
struct Node *Reverse(struct Node *node) {
    struct Node *prev = NULL;
    while (node != NULL) {
        struct Node *next = node->next;
        node->next = prev;
        prev = node;
        node = next;
    }
    return prev;
}

// 判断回文链表 O(1) 空间复杂度
bool IsPalindromic(struct Node *node) {
    struct Node *head = node;
    struct Node *mid = Middle(node);
    struct Node *tail = Reverse(mid);

    // 从头、尾对向比较
    struct Node *n1 = head, *n2 = tail;
    while (n1 != NULL && n2 != NULL) {
        // 奇数情况下：两边一样长
        // 偶数情况下，左边比右边短一位
        // 综合判断 n1 && n2 都非空，无碍
        if (n1->v == n2->v) {
            n1 = n1->next;
            n2 = n2->next;
        } else {
            return false;
        }
    }
    return true;
}

链表区间反转 ¶

问题：反转单链表中位于区间 [left, right] 的部分。

例如，1->2->3->4->5 反转区间 [2,4] 后是 1->4->3->2->5 。

leetcode 题目 - 反转链表 II

此外，算法应尽量只扫描链表一次。

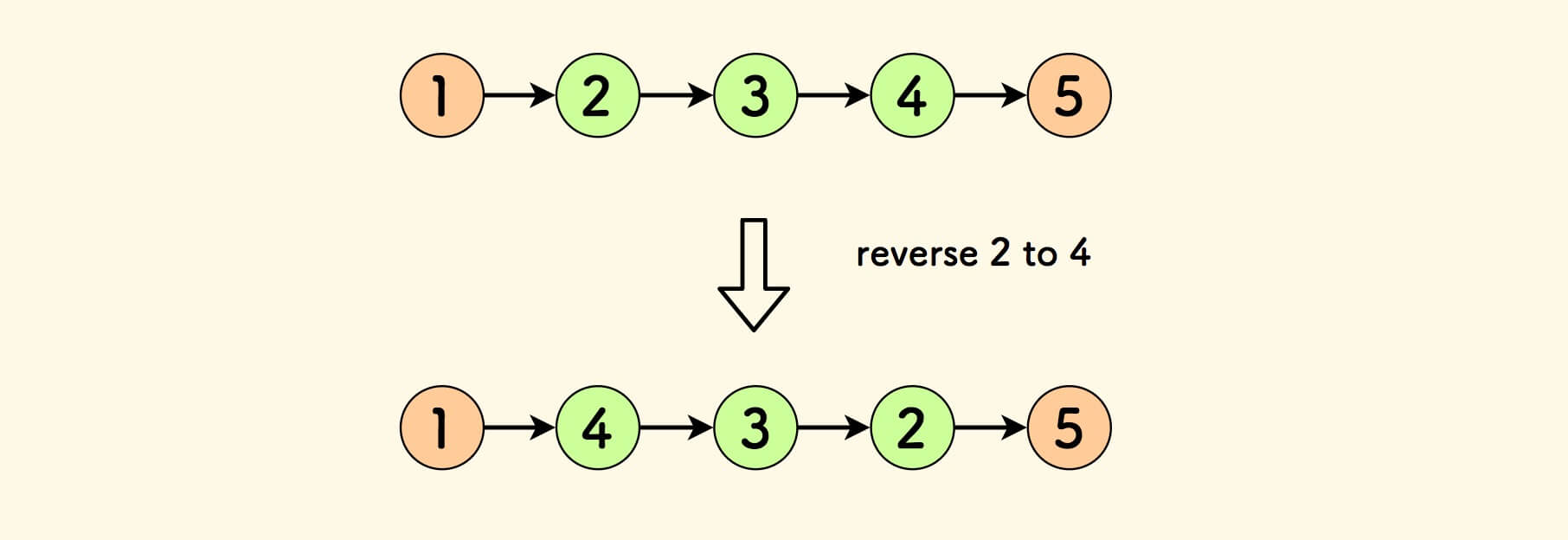
两种思路：头插法和反转区间再拼接的思路。

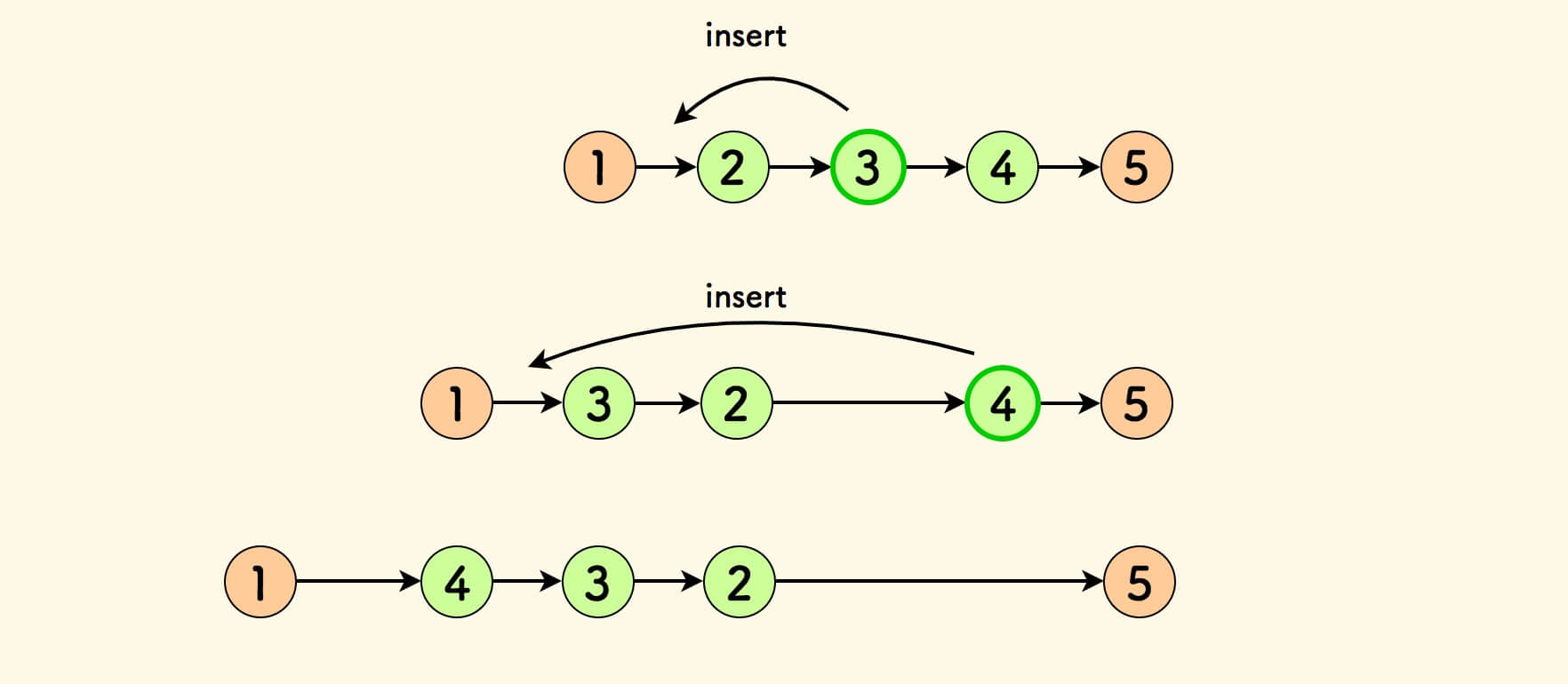
头插法

把区间内的节点不断的插到区间头前面。

一个细节是，头节点可能发生变化，可以虚拟一个头节点，来简化处理。

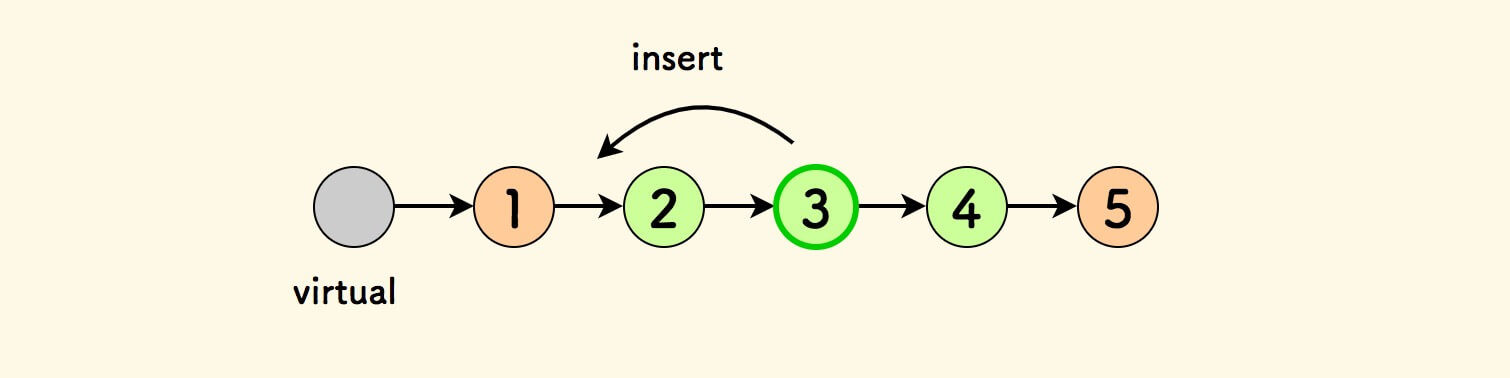
插入的细节动作如下图所示：

先挪走当前节点。
然后放入左边界节点前面，缝接好。

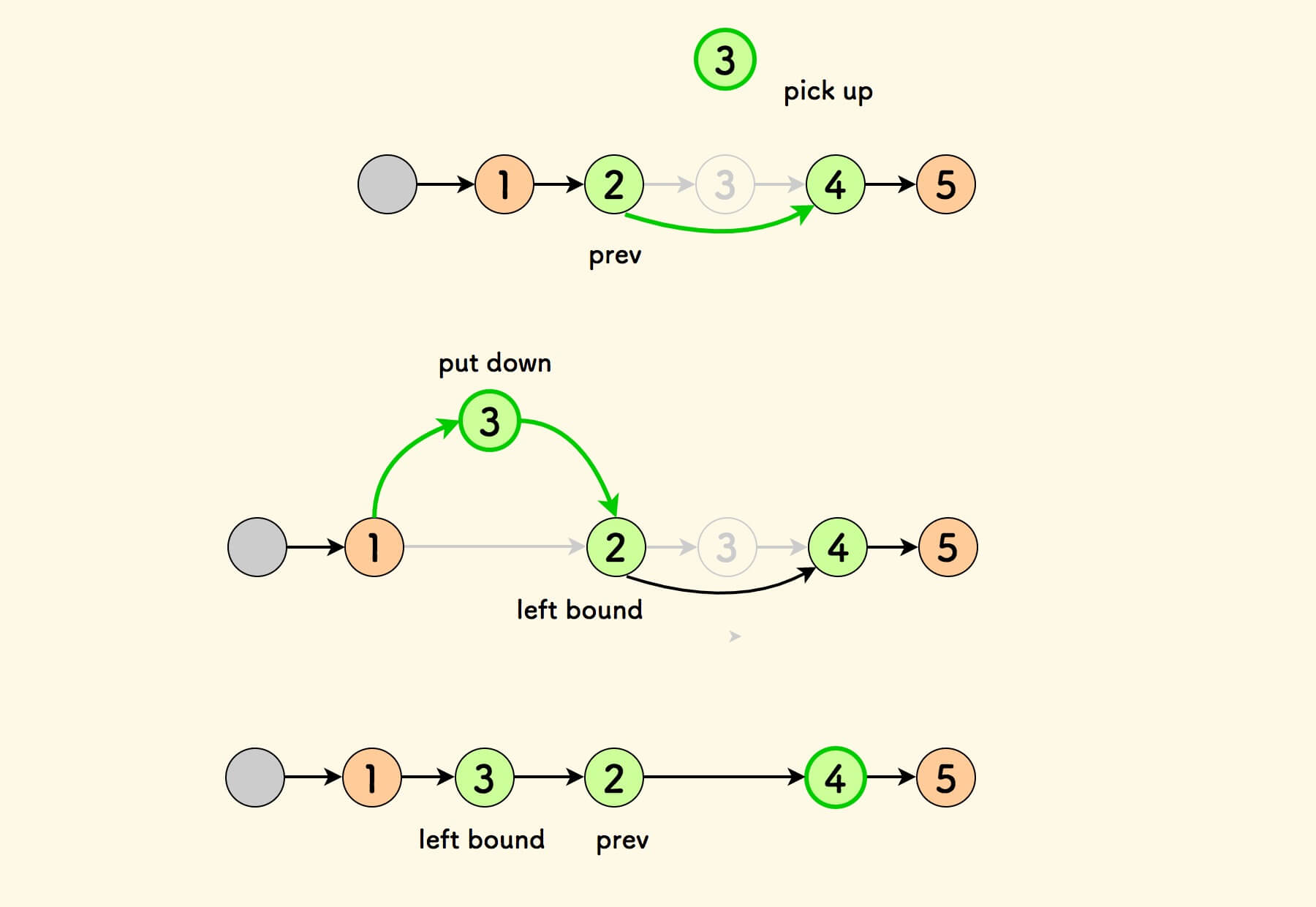
链表区间反转 - 头插法 - C 语言实现

// 反转链表的一个区间 ，头插法
struct Node *ReverseInterval(struct Node *head, int left, int right) {
    struct Node *virtual_head = &(struct Node){0, head};
    struct Node *node = head;
    struct Node *prev = virtual_head;     // node 的前驱节点
    struct Node *left_bound = NULL;       // 左边界节点
    struct Node *left_bound_prev = NULL;  // 左边界节点的前驱节点

    int i = 1;

    while (node != NULL && i <= right) {
        struct Node *node_next = node->next;

        if (i == left) {
            // 初始化左边界
            left_bound = node;
            left_bound_prev = prev;
        }

        if (i > left) {  // 插入左边界之前
            prev->next = node->next;
            node->next = left_bound;
            // 此时 i > left ，说明 i == left 肯定已执行
            // left_bound_prev 必定非空
            left_bound_prev->next = node;
            // 更新左边界
            left_bound = node;
        } else {
            // 注意，只有在没有挪走 node 的时候才需要更新 prev
            prev = node;
        }

        node = node_next;
        i++;
    }

    return virtual_head->next;
}

反转后再缝接

另一种思路是：

找到左右边界 LP 和 RN 。
反转区间内链表。
左右边界颠倒地对区间进行缝接。

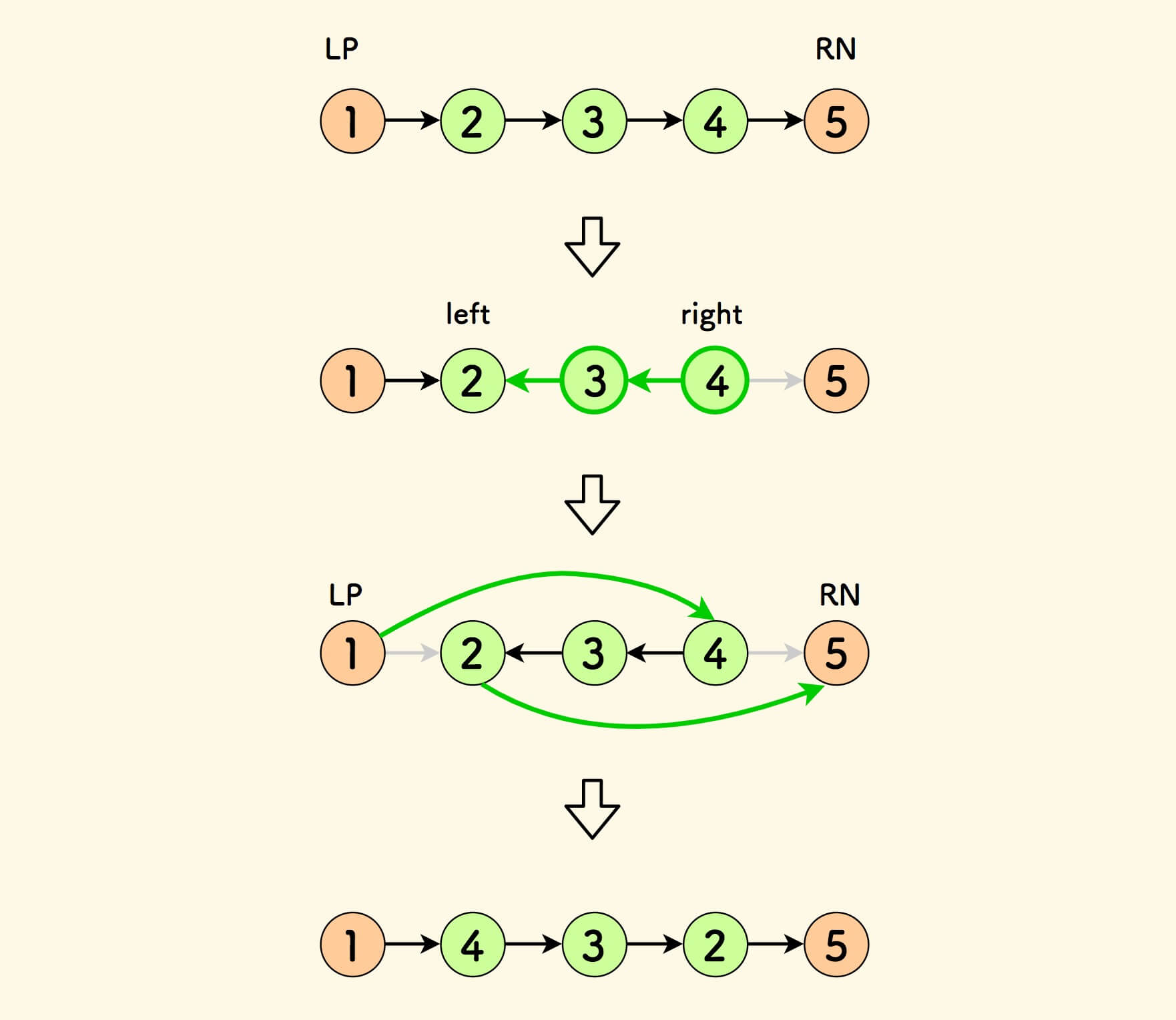
其中：

LP 是位置为 left 节点的前驱节点。
RN 是位置为 right 节点的后置节点。

此方法，仍然只需要一次扫描。

链表区间反转 - 反转后再缝接 - C 语言实现

// 反转链表的一个区间
struct Node *ReverseInterval(struct Node *head, int left, int right) {
    struct Node *node = head;
    struct Node *prev = NULL;
    struct Node *left_bound = NULL;   // 左边界节点
    struct Node *right_bound = NULL;  // 右边界节点
    struct Node *left_prev = NULL;    // 左边界前面的节点
    struct Node *right_next = NULL;   // 右边界后面的节点

    int i = 1;

    while (node != NULL && i <= right) {
        struct Node *node_next = node->next;

        if (i == left) {  // 记住左边界
            left_bound = node;
            left_prev = prev;
        }

        if (i == right) {  // 记住右边界
            right_bound = node;
            right_next = node_next;
        }

        // 中间区间 (left, right] 进行反转
        if (i > left && i <= right) node->next = prev;

        prev = node;
        node = node_next;
        i++;
    }

    // 缝接到原链表上
    if (left_prev != NULL) left_prev->next = right_bound;
    if (left_bound != NULL) left_bound->next = right_next;
    if (left_prev != NULL) return head;
    return right_bound;
}

链表分割 ¶

问题：单链表中的每个节点上的数据都是一个数字。给定一个数字 $k$ ，对链表进行分割，使得分割后，数值小于 $k$ 的节点都在左边，大于等于 $k$ 的节点都在右边。

此外，需要保留两个分区中每个节点的初始相对顺序。

例如：链表 1->4->3->2->5->2 ，按 $k=3$ 分割的结果可以是 1->2->2->4->3->5 。

leetcode 题目 - 分割链表

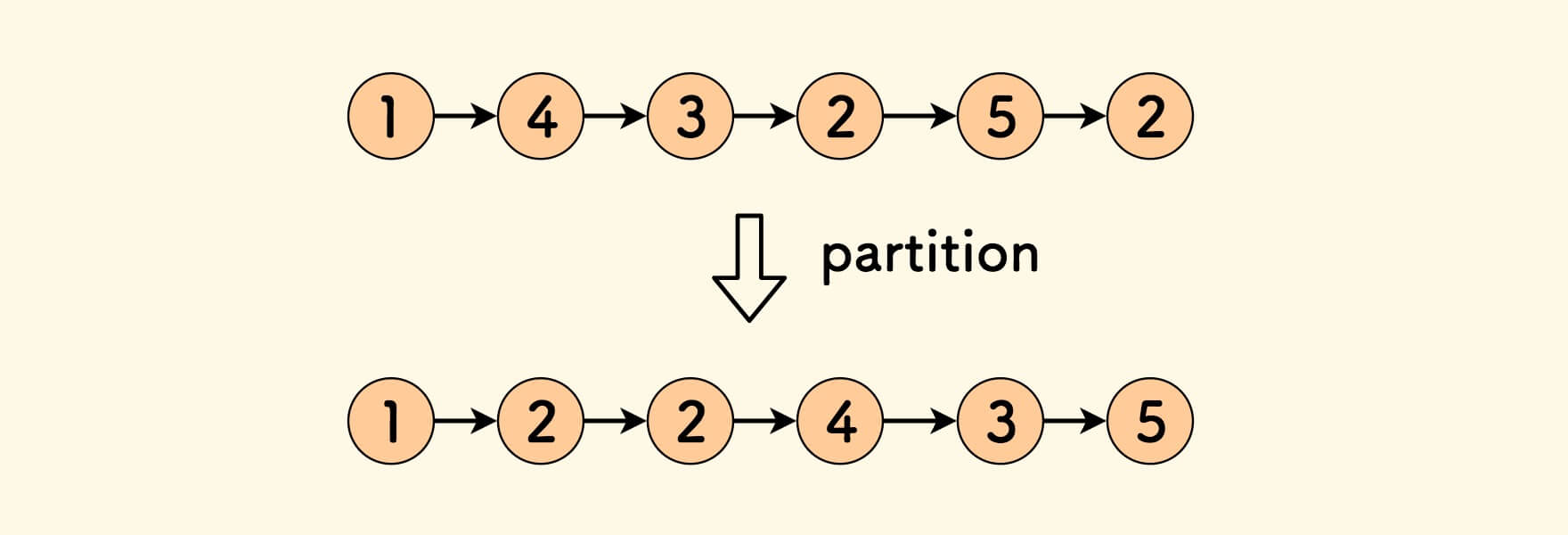
链表分割的问题和数组原地分割的问题类似，不过数组原地分割是不保序的。

这个问题有两种思路：插入的思路、合并的思路。

插入的思路

采用一个慢指针 slow 和快指针 fast 迭代链表：

慢指针永远指向当前小于 $k$ 的最后一个节点。
快指针正常地、一步一步地向前滑动。
快指针遇到小于 $k$ 的节点，就把它插入到慢指针后面来。

总而言之：把小于 $k$ 的节点往前提。

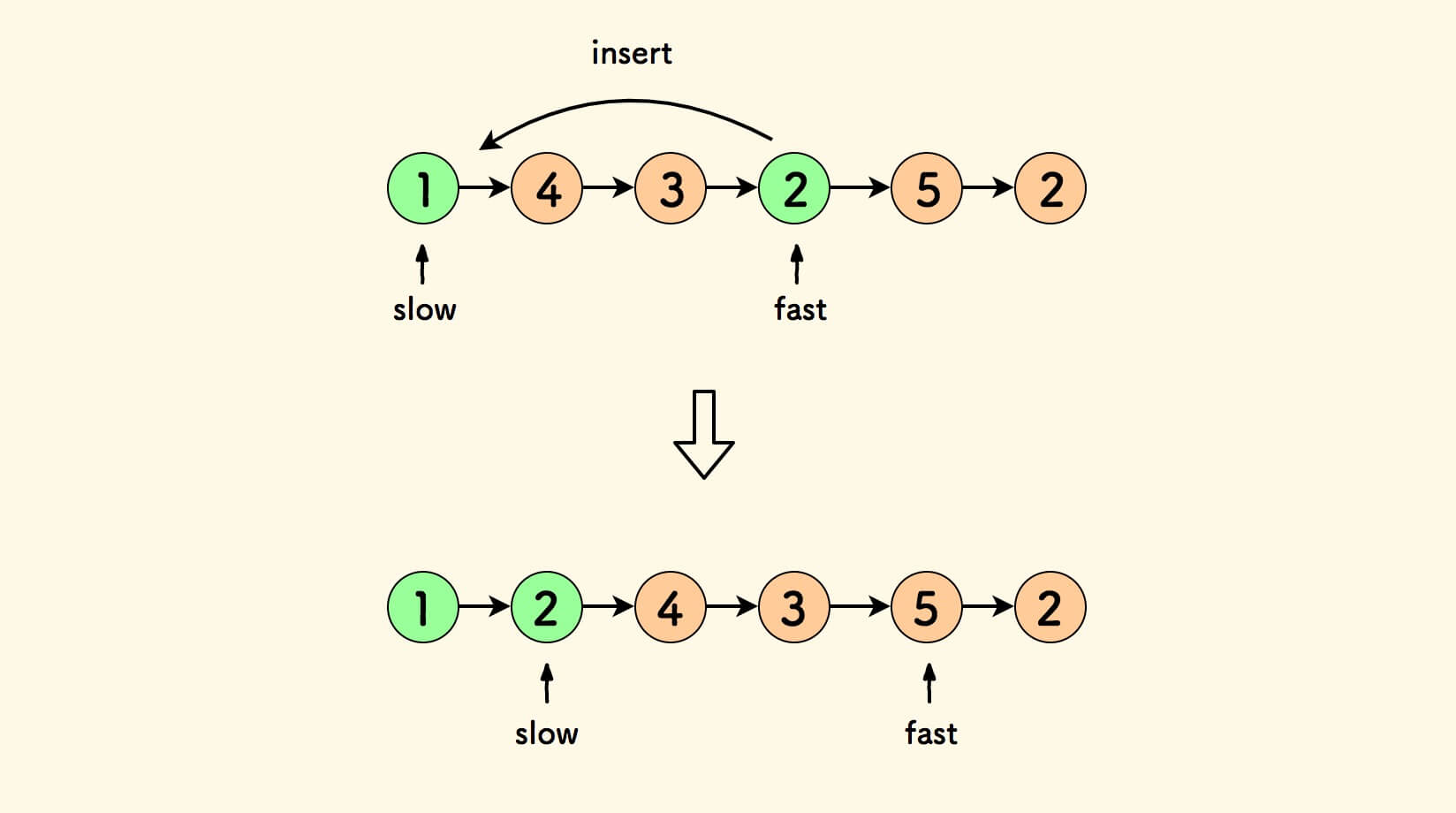
细节的插入动作是这样的：

先把 fast 指向的节点移除出来。
再插入到 slow 指向的节点后面。

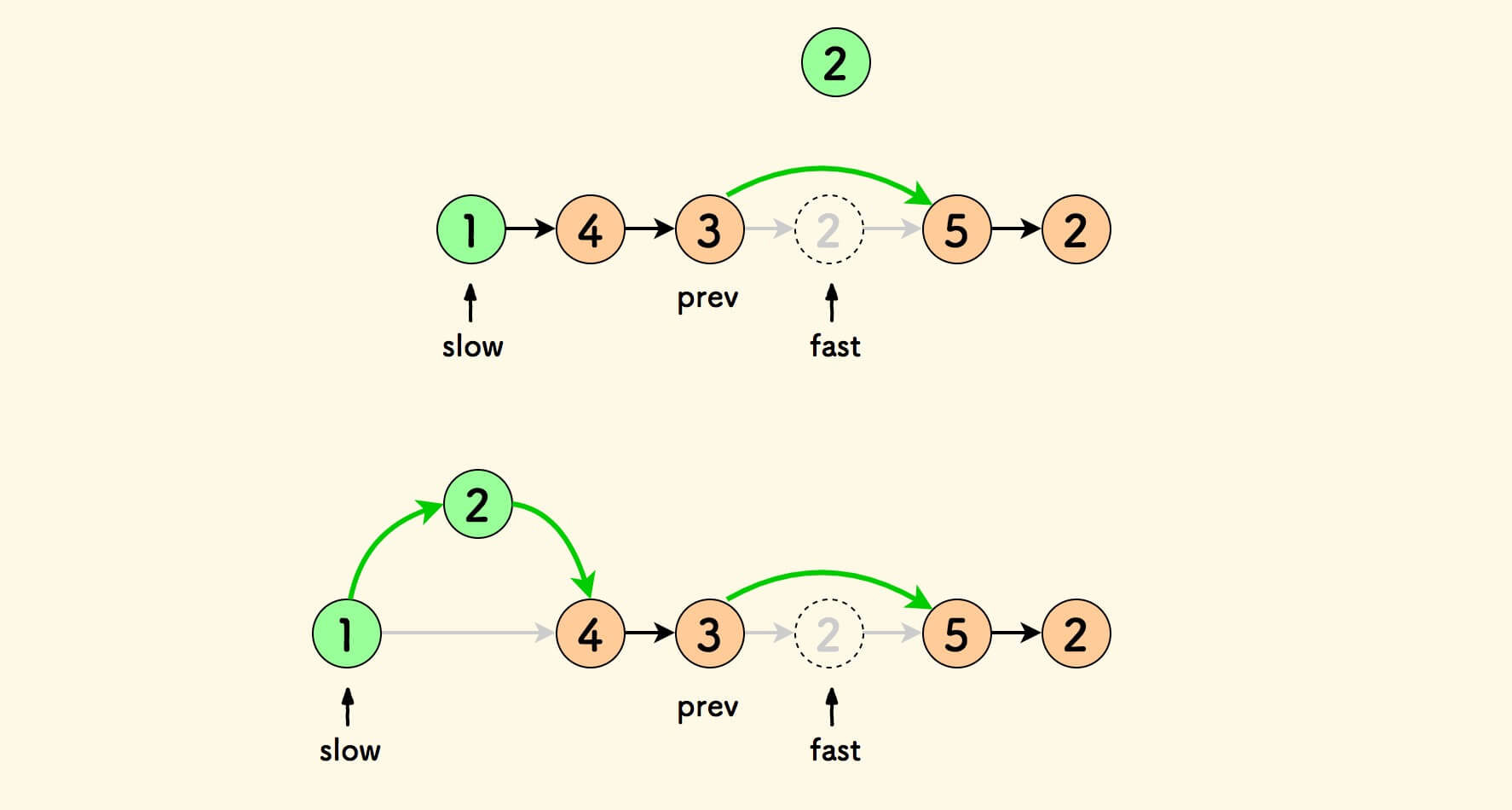
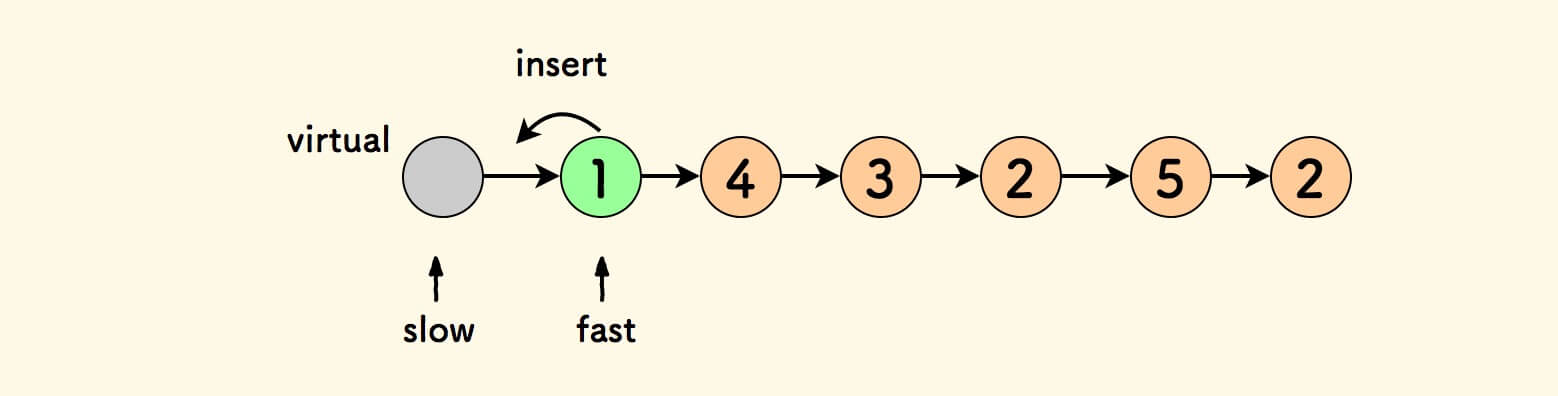
另外，指针 slow 应如何初始化呢？

为了简化操作，不妨放置一个虚拟的头节点，如此一来，就不必考虑 slow 节点的初始化问题了。

最终返回虚拟节点的后置节点就行了。

分割链表 - 插入的思路 - C 语言实现

struct Node *Partition(struct Node *head, int k) {
    // slow_head 是虚拟头节点，指向 head
    struct Node *slow_head = &(struct Node){0, head};
    struct Node *slow = slow_head;  // slow 指向目前 <k 的节点
    struct Node *fast = head;       // fast 一步一个节点迭代
    struct Node *prev = head;       // fast 的前驱节点

    while (fast != NULL) {
        struct Node *fast_next = fast->next;
        if (fast->v < k) {
            // 移除当前节点 fast
            if (prev != NULL) prev->next = fast_next;
            // 放入到 slow 节点之后
            if (slow->next != fast) {
                fast->next = slow->next;
                slow->next = fast;
            }
            slow = fast;
        } else {
            // 只有不挪走 fast 的时候才更新 prev
            prev = fast;
        }
        fast = fast_next;
    }
    return slow_head->next;
}

合并的思路

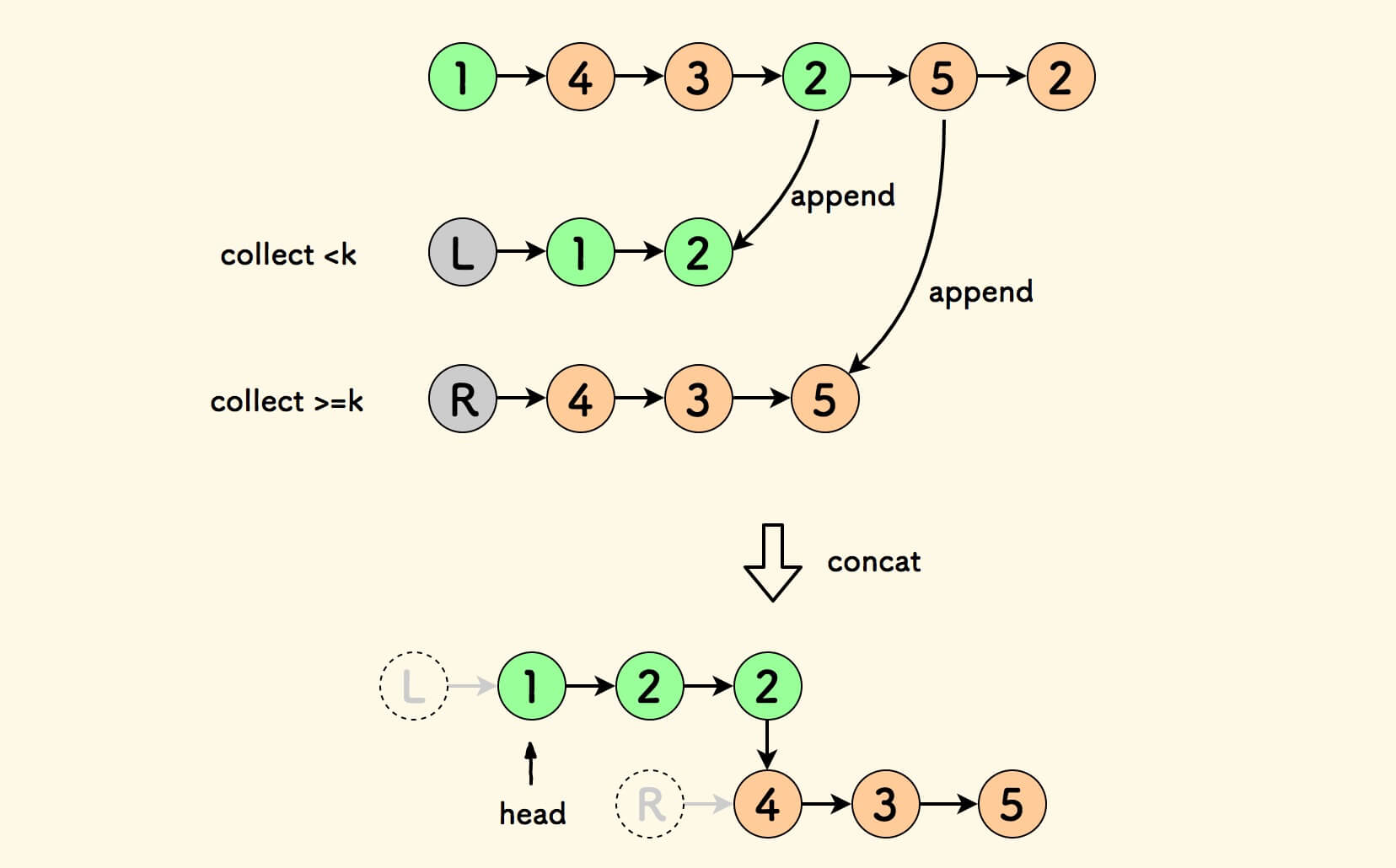
合并的思路，比插入的思路理解起来要简单：

新增两个单链表，头节点分别是 L 和 R。
把小于 $k$ 的节点拣到链表 L 中。
把大于等于 $k$ 的节点拣到链表 R 中。
合并两个链表 L 和 R ，并舍弃两个虚拟节点头。

总而言之，把节点分类到两个链表中，然后再拼接。

这个思路理解起来简单，而且需要关心的细节处理并没有前一个思路那么多。

分割链表 - 合并的思路 - C 语言实现

struct Node *Partition(struct Node *head, int k) {
    struct Node *left_head = &(struct Node){0, NULL};
    struct Node *right_head = &(struct Node){0, NULL};

    struct Node *node = head;         // 迭代原链表
    struct Node *left = left_head;    // 迭代左链表
    struct Node *right = right_head;  // 迭代右链表

    while (node != NULL) {
        if (node->v < k) {
            // 拣到左边链表
            left->next = node;
            left = left->next;
        } else {
            // 拣到右边链表
            right->next = node;
            right = right->next;
        }
        node = node->next;
    }
    // 末尾抹 NULL
    right->next = NULL;
    // 拼接，并丢弃 right_head
    left->next = right_head->next;
    // 返回左起第二个元素即原链表中的节点
    return left_head->next;
}

链表合并 ¶

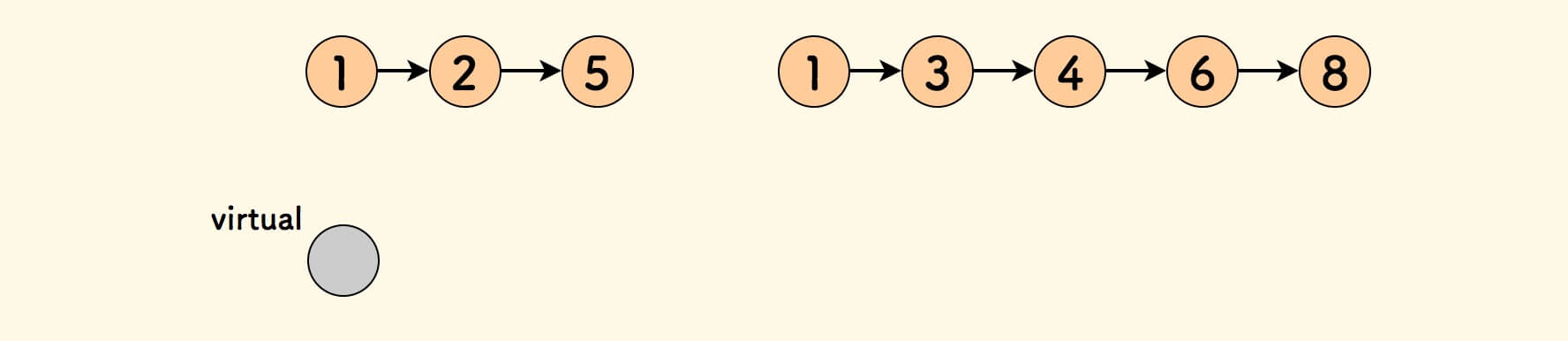
问题：合并两个有序链表，使得合并后的链表也是有序的，要求原地操作。

例如：合并 1->2->5 和 1->3->4->6->8 的结果是 1->1->2->3->4->5->6->8 。

leetcode 题目 - 合并两个有序链表

在归并排序算法中有一个基础操作是合并两个有序数组，链表的合并思路和它完全一致。

新建一个临时头节点，它拉起合并后的链表。
从两个链表中分别取出一个节点，把其中数字更小的拿出来追加到新链表上，另一个大的节点不拿出来。
重复第二部，直到其中一个链表全部拿完。
新链表的尾巴节点，指向剩下的那个链表没拿完的部分即可。
最后丢弃临时头节点，即完成合并。

合并两个有序链表 - C 语言实现

struct Node *MergeSortedList(struct Node *a, struct Node *b) {
    struct Node *head = &(struct Node){0, NULL};  // 临时头节点
    struct Node *prev = head;                     // c 的前驱节点
    struct Node *c = NULL;

    // 合并
    while (a != NULL && b != NULL) {
        if (a->v <= b->v) {
            c = a;
            a = a->next;
        } else {
            c = b;
            b = b->next;
        }
        prev->next = c;
        prev = c;
    }

    // 至多还有一个没有迭代完的链表
    if (a != NULL) prev->next = a;
    if (b != NULL) prev->next = b;

    return head->next;
}

显然，其时间复杂度是 $O(m+n)$ ，空间复杂度是 $O(1)$ 。

链表排序 ¶

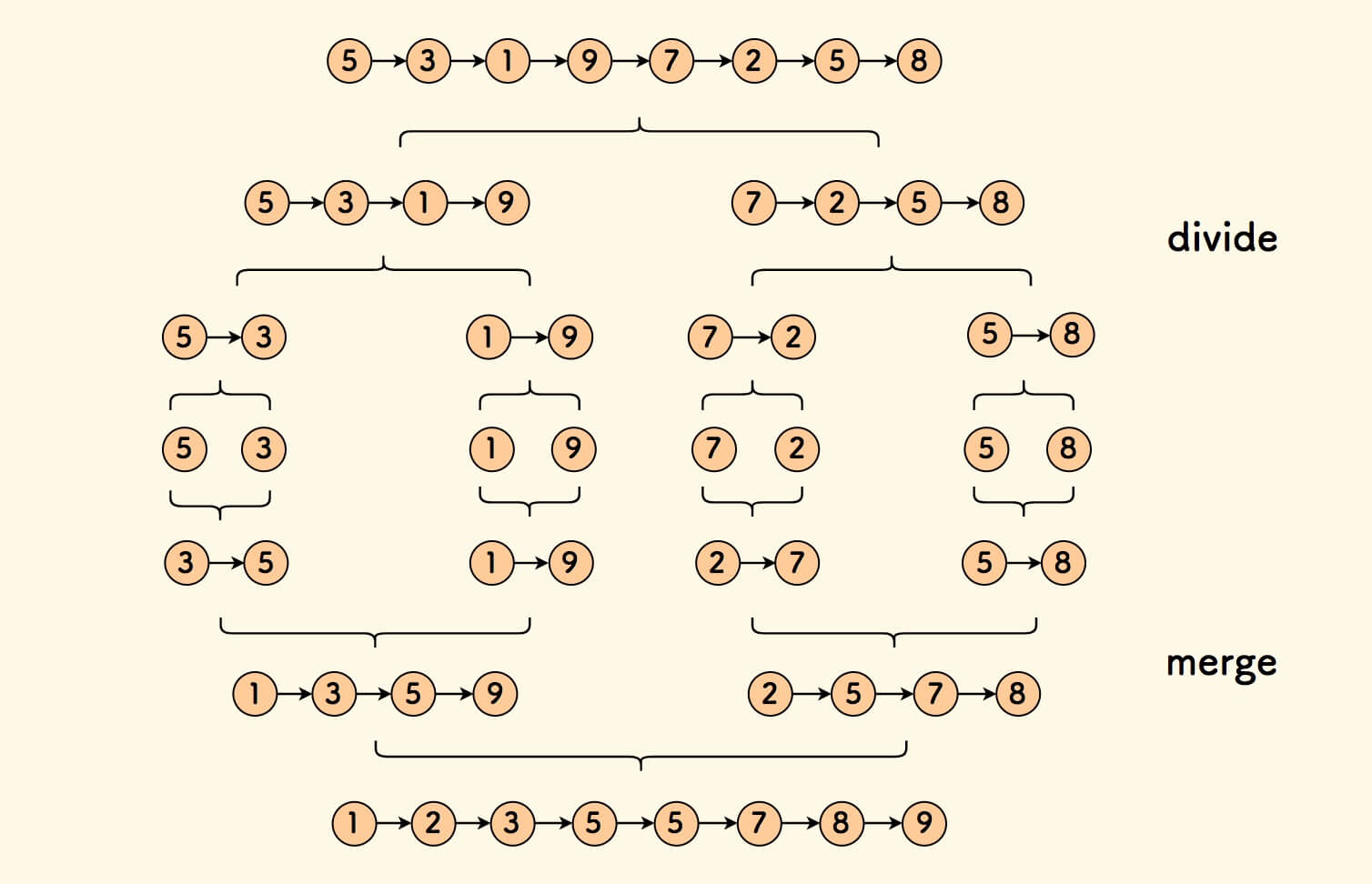
基于上面的有序链表合并算法，可以进一步得出链表的归并排序算法。

找出链表的中间节点，以此为界，二分为左右两个链表。
递归二分下去，直到每一份链表只有一个节点。
相邻的链表归并，递归进行，即得整个链表有序。

和数组上的归并排序过程是一样的，是递归的合并有序链表的过程。

总的来说，先分后合。

链表归并排序 - C 语言实现

struct Node *Sort(struct Node *node) {
    // 递归终止
    if (node == NULL || node->next == NULL) return node;

    // 找出中间的节点
    struct Node *mid = Middle(node);
    // 拆分为左右两个链表
    struct Node *a = node;
    // 此时至少两个节点, mid 必然有后节点
    struct Node *b = mid->next;
    // 左边链表以 mid 结尾，封死其结尾
    mid->next = NULL;

    // 递归
    struct Node *a1 = Sort(a);
    struct Node *b1 = Sort(b);

    // 合并
    return MergeSortedList(a1, b1);
}

递归深度是 $\log{n}$ ，每一次二分和归并的时间复杂度都是 $O(n)$ 。

因此链表的归并排序的总时间复杂度也是 $O(n\log{n})$ 。

不过，和数组的归并排序不同，链表的归并排序的空间复杂度是 $O(1)$ 。

链表相交 ¶

问题：找出两个单链表的第一个公共节点。

例如：a->b->c->d->e 和 f->g->d->e 的第一个交点是 d 。

leetcode 题目 - 两个链表的第一个公共节点

这是一个非常经典的链表问题。

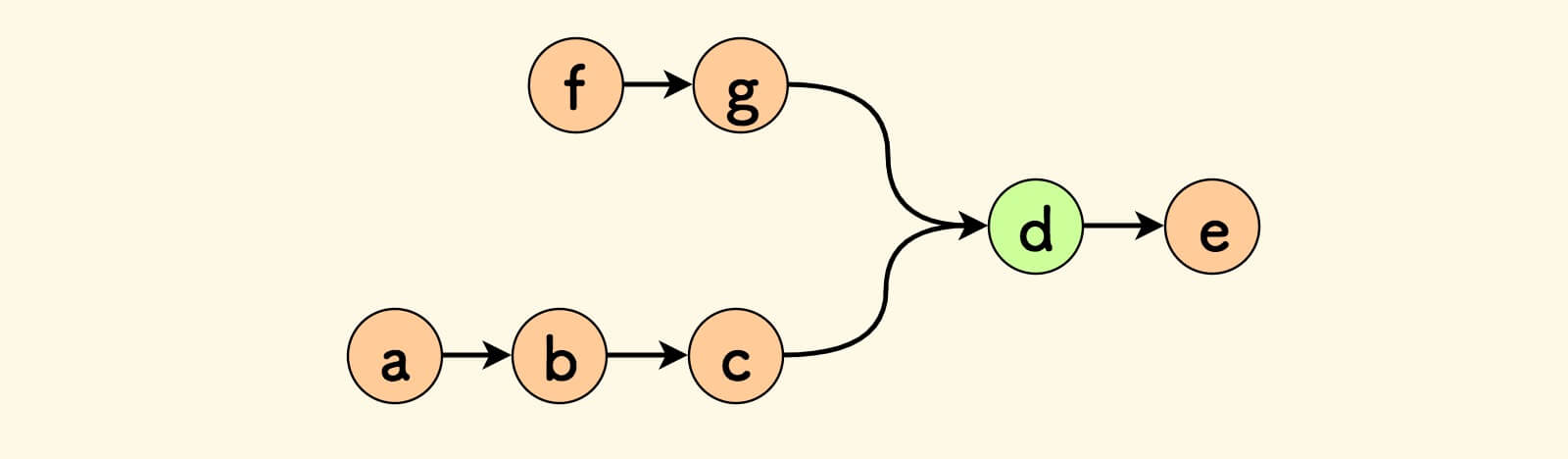
这个问题也有两种思路：延迟指针方法、双指针交替方法。

延迟指针方法

用一个红色、蓝色指针分别迭代两个链表。
直到有一个到达终点。
不妨设，蓝色是短一些的链表的迭代指针。
此时从长链表的起点，再发出一个黄色指针。
红色指针继续行进，直到它到达终点。
此时黄色指针的位置，恰好和短链表对齐。
再从短的链表发出一个绿色指针。
绿色和黄色指针齐头并进，直到相遇，就是交点。

总结来说，先找一个指针对齐短链表，之后相遇节点就是交点。

此方法的代码实现从略。

双指针交替方法

这个问题更为流行、也更为漂亮的解法，是双指针交替的方法。

首先，不妨将两个链表的节点染色：红色、蓝色、绿色。

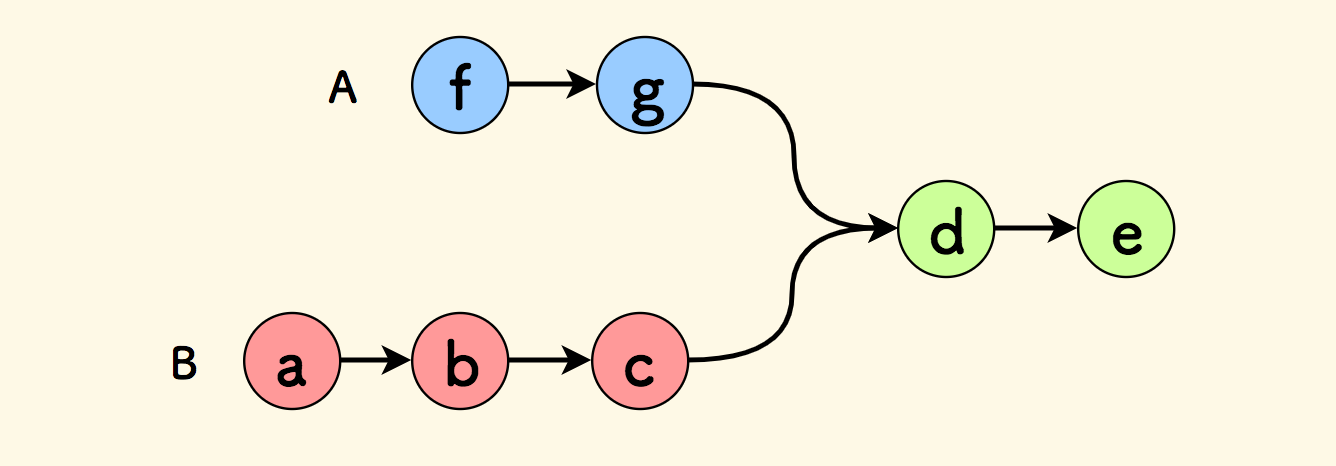
将两个链表拉平来看：

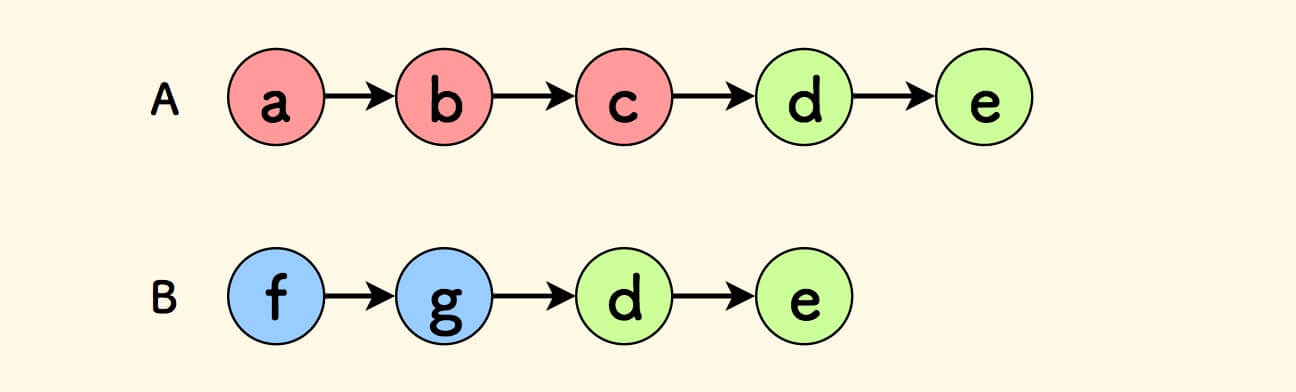
把一个链表追加到另一个链表来看：

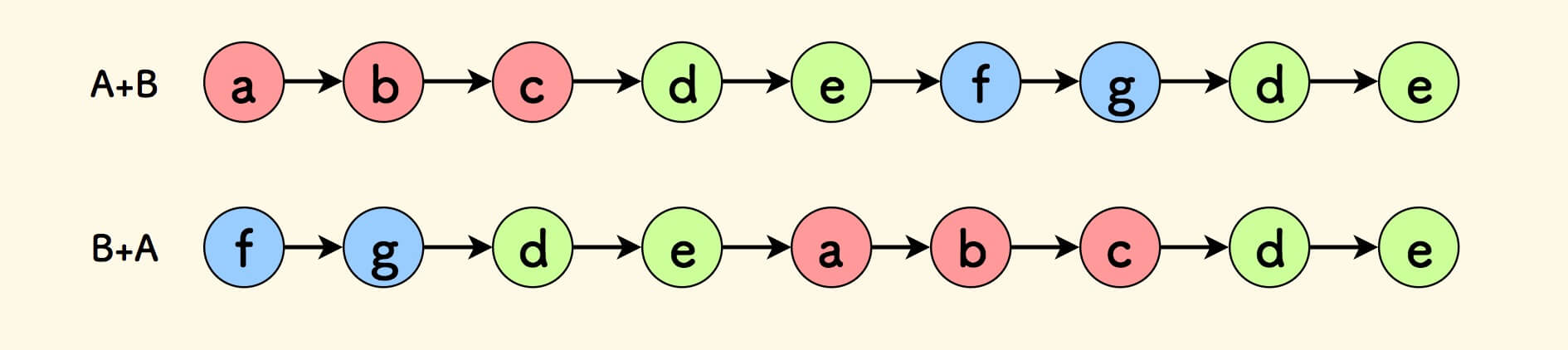
意味着，如果两个指针沿着 A+B 的路径和 B+A 的路径，同步迭代，就会找到相交点。

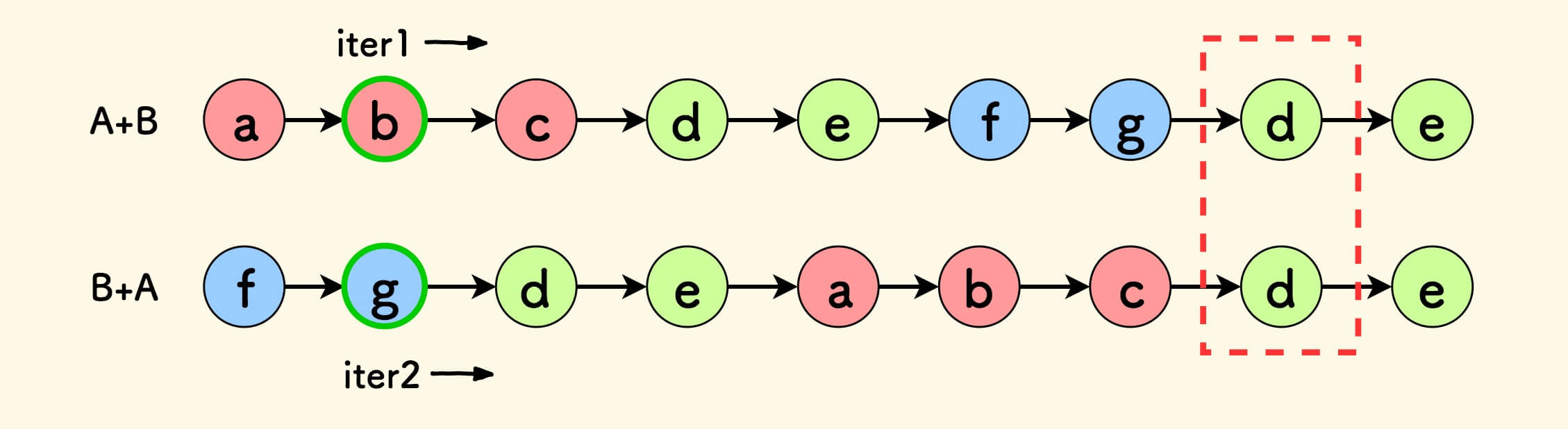
A+B 和 B+A 的路径的意思是：

一个指针从链表 A 的头出发，到尾节点时，进入 B 迭代。
一个指针从链表 B 的头出发，到尾节点时，进入 A 迭代。

当两个指针相遇时，就找到了相交节点。

从图上也可以看到指针迭代的次数，必然不超过 M+N 。

另外，如果交点是 NULL ，就说明没有交点。

链表交点 - C 语言实现

// 找出两个单链表的交叉点，没有交叉点则返回 NULL
struct Node *Intersection(struct Node *a, struct Node *b) {
    struct Node *na = a;
    struct Node *nb = b;

    while (na != nb) {
        if (na != NULL) na = na->next;
        else na = b;

        if (nb != NULL) nb = nb->next;
        else nb = a;
    }
    return na;
}

链表查环 ¶

判断单链表是否有环

首先，如何判断单链表是否存在环？

例如：a->b->c->d->e->f->g->c 就存在环。

leetcode 题目 - 环形链表

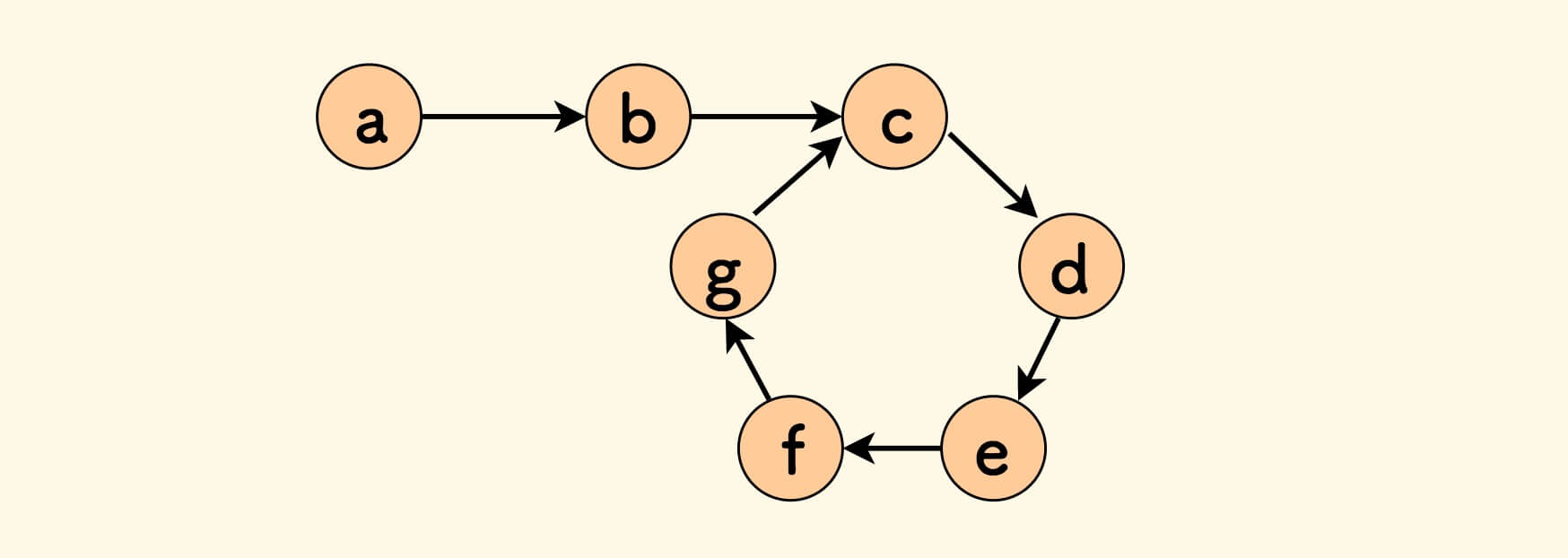
这同样是链表的一个经典算法问题，采用龟兔判圈算法：

起两个指针迭代链表，一快一慢，快的一次走两步，慢的一次走一步。
当两个指针相遇时，即存在环。
否则，如果迭代完仍未相遇，则不存在环。

这个算法的原理？

许多人用数学来说明，这里将采用更通俗的方式，一图胜千言。

如果链表不存在环，容易知道，快慢指针永不相遇。

对于有环链表，将说明必然相遇。

把链表以螺旋状展示，螺旋的每一层长度是环的长度。

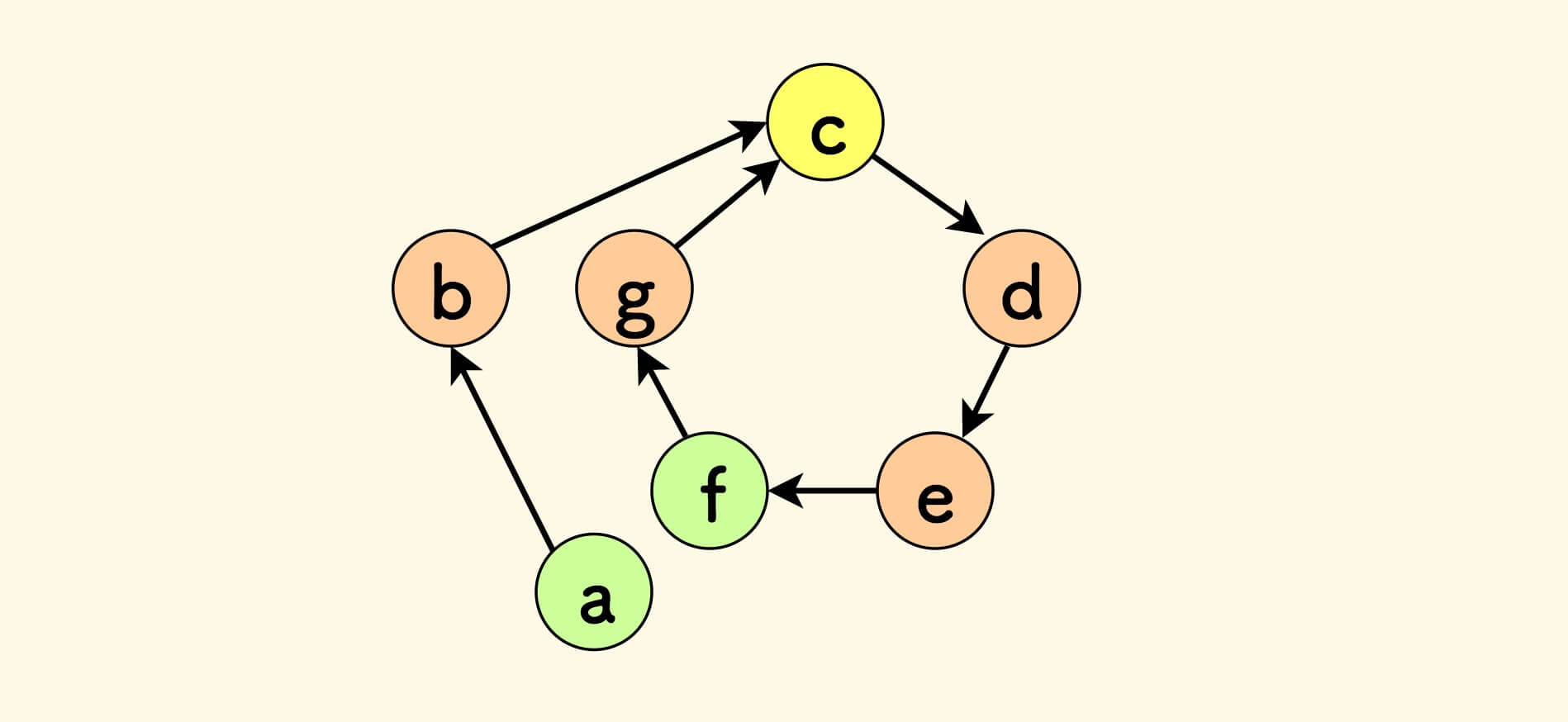
可以知道：当慢指针走一圈到达 f 时，快指针已经进入环内，并且已经转了一圈，同样到达 f 。

此时，快慢指针相遇。

可以再看一个更大一些的例子：

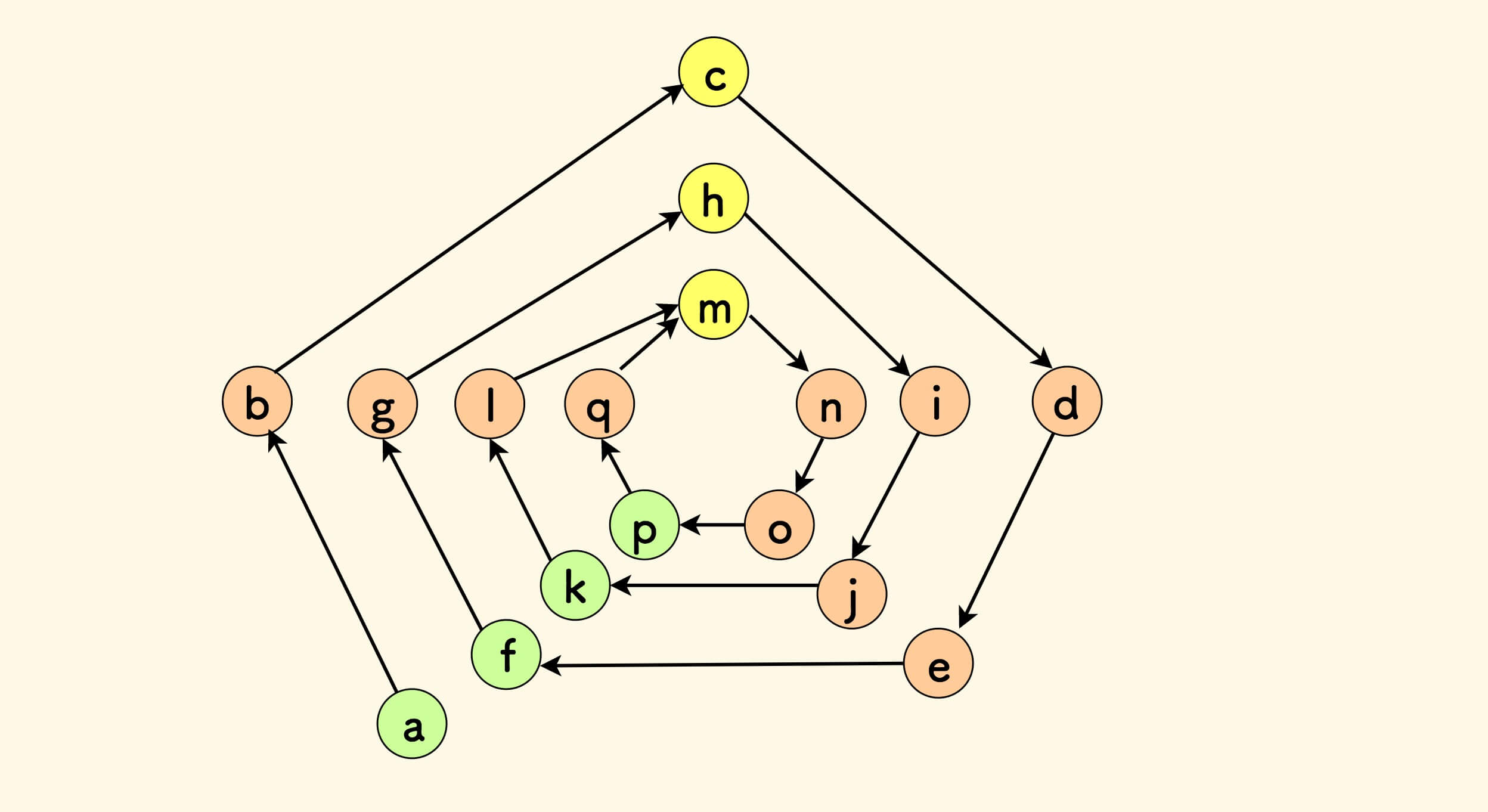
当慢指针走一圈到达 f 时，快指针已经到达 k 。
当慢指针走一圈到达 k 时，快指针已经到达 p ，且已经在环上转了一圈。
当慢指针走一圈到达 p 时，快指针又转两圈，到达 p ，二者相遇。

总之，有环必相遇，无环永不相遇。

此外，还可以发现，慢指针最多在环上走一圈，即可与快指针相遇，时间复杂度必 $O(n)$ 。

单链表判断是否有环 - C 语言实现

// 判断单链表是否存在环
bool HasCycle(struct Node *node) {
    struct Node *slow = node;
    struct Node *fast = node;

    while (fast != NULL && fast->next != NULL) {
        slow = slow->next;
        fast = fast->next;
        fast = fast->next;
        if (slow == fast) return true;
    }
    return false;
}

找出环的入口

进一步地，如何找到环的入口呢？

leetcode 题目 - 环形链表 II

方法：

采用两个慢指针，一个从头出发，一个从相遇节点出发。
齐头并进，一次一步，相遇处即环的入口。

从上面的图，已经知道相遇点和头节点的位置关系。

仍然采用螺旋层数较多的例图进行说明。

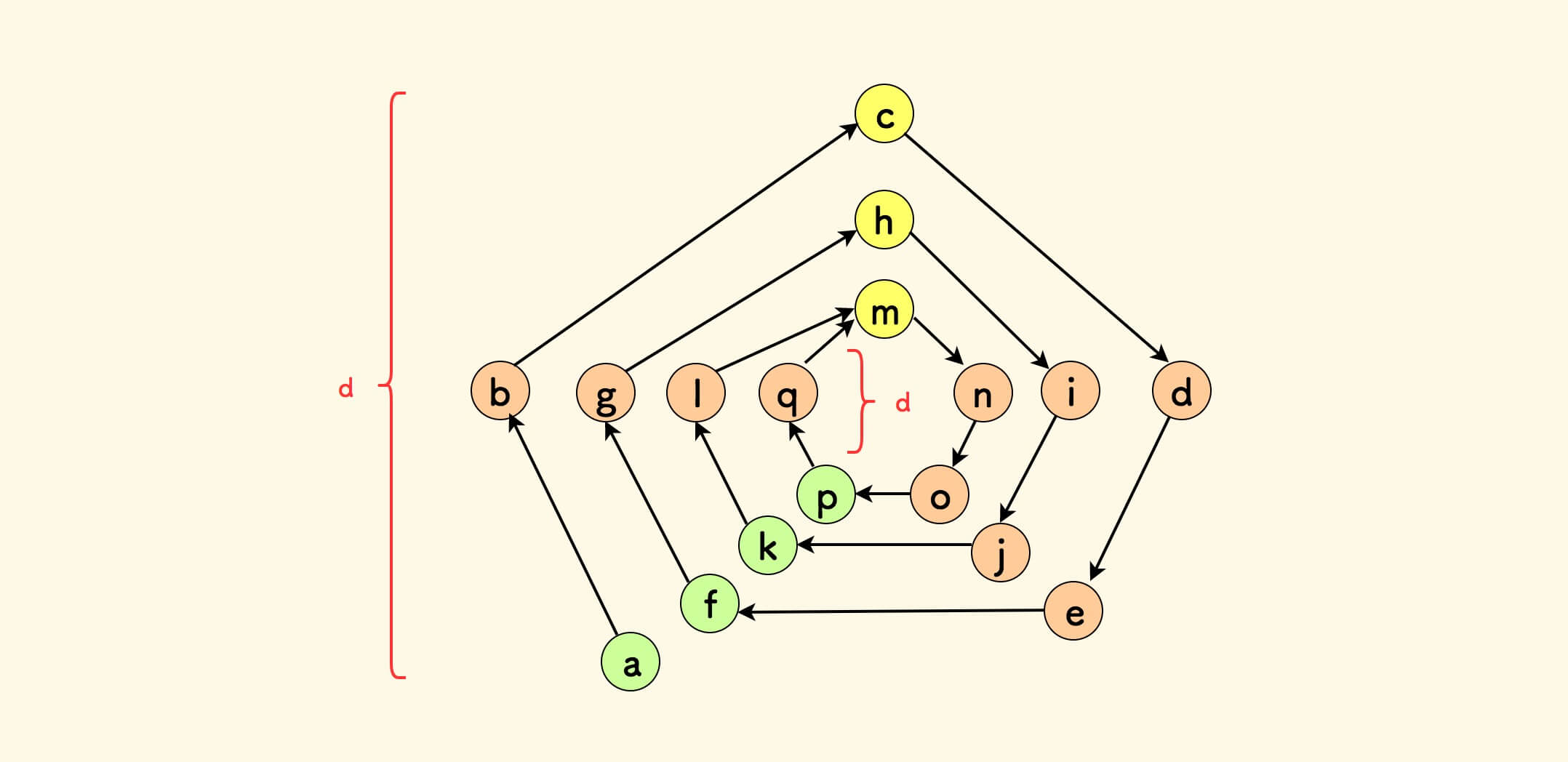
假设入口节点是 m ，相遇点 p 到环入口 m 的距离是 d 。

找出螺旋上最外层对应 m 的节点 c ，它和头节点 a 的距离也是 d 。

那么 a 和 m 的距离就是 (N-1) * c + d ，其中 c 表示环周长，N 表示螺旋层数。

推演过程：

外层慢指针从 a 出发，经过 N-1 层后到达节点 k 。
同步地，最内层环上的慢指针从相遇点 p 出发，空转 N-1 圈。
两个慢指针分别从 k 和 p 出发，经过 d 步必然在 m 处相遇。

找出单链表环的入口节点 - C 语言实现

// 如果单链表存在环，返回其入口节点
struct Node *CycleEntry(struct Node *node) {
    // 找到相遇节点，同 HasCycle
    struct Node *slow = node;
    struct Node *fast = node;

    while (1) {
        if (fast == NULL || fast->next == NULL) return NULL;
        slow = slow->next;
        fast = fast->next;
        fast = fast->next;
        if (slow == fast) break;
    }

    // slow 是相遇节点, fast 重置到头，各自一步一步走
    fast = node;
    while (fast != NULL && slow != NULL) {
        if (slow == fast) return slow;
        slow = slow->next;
        fast = fast->next;
    }
    return NULL;
}

有趣。

（完）

本文的所有代码 On Github